2PY 2023 vår LØSNING LK20: Forskjell mellom sideversjoner
| Linje 54: | Linje 54: | ||
====a)==== | ====a)==== | ||
Mønsteret er at hver figur øker totalt med fire sirkler i forhold til forrige figur. | |||
Figur nr. 4 har 17 sirkler, og figur nr. 5 har 21 sirkler. | Figur nr. 4 har 17 sirkler, og figur nr. 5 har 21 sirkler. | ||
| Linje 60: | Linje 60: | ||
====b)==== | ====b)==== | ||
For å bestemme et uttrykk må vi finne mønsteret. | For å bestemme et uttrykk må vi finne mønsteret for antall sirkler i hver figur. | ||
Figur nr. 1 har 4 + 1 sirkler. | Figur nr. 1 har 4 + 1 sirkler. | ||
Sideversjonen fra 4. okt. 2023 kl. 17:31
Diskusjon av oppgaven på matteprat
Løsningsforslag av Jon Bjarne Bø
DEL 1
Oppgave 1
a)
Prisen for brødet steg med 42-40 = 2 kroner.
Prosent endring = endring / opprinnelig verdi.
Jeg regner ut prosent økning for prisen til brødet:
$\frac{2}{40}=\frac{1}{20}=0,05 = 5$ %
Prisen til brødet steg altså med 5 %.
b)
Det er påstand 2) som er riktig, prisen vil stige med mindre enn 5 % hvert år. Dette er fordi prisen blir stadig høyere, og 2 kroner av en stadig høyere pris, utgjør en stadig lavere prosentandel av prisen.
Oppgave 2
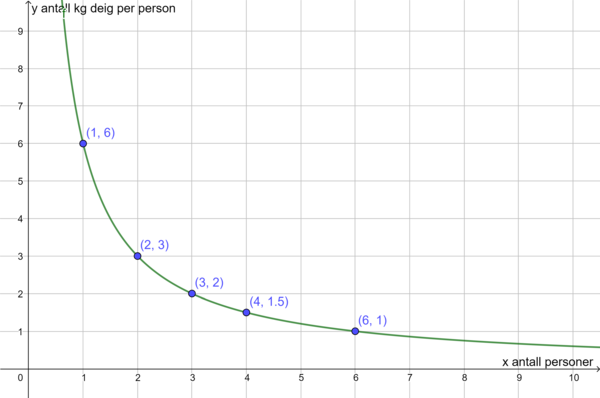
Antall kg deig per person (y) er omvendt proporsjonalt med antall personer (x). Vi har y=6/x
Siden dette er del 1 av eksamen, må du lage en grafisk fremstilling på papir.
Oppgave 3
a)
At den relative frekvensen for å ha to søsken er 0,4, betyr at 40 % av klassen har to søsken.
At den kumulative frekvensen for to søsken er 16, betyr at 16 elever i klassen har 0, 1 eller 2 søsken.
b)
Ingen elever har 0 søsken. Fire elever har 1 søsken.
Det vil si at 16-4 = 12 elever har 2 søsken. Dette utgjør 40 % av elevene.
Det vil si at 10 % utgjør 3 elever, altså vil det si at 100 % av elevene er 30 elever. Det er 30 elever i klassen til Truls og Thea.
Oppgave 4
a)
Mønsteret er at hver figur øker totalt med fire sirkler i forhold til forrige figur.
Figur nr. 4 har 17 sirkler, og figur nr. 5 har 21 sirkler.
b)
For å bestemme et uttrykk må vi finne mønsteret for antall sirkler i hver figur.
Figur nr. 1 har 4 + 1 sirkler.
Figur nr. 2 har 4*2 + 1 sirkler.
Figur nr. 3 har 4*3 + 1 sirkler.
...
Figur nr. n har 4*n + 1 sirkler.
Et uttrykk for antall sirkler i figur n er: $F_n=4n+1$
DEL 2
Oppgave 2
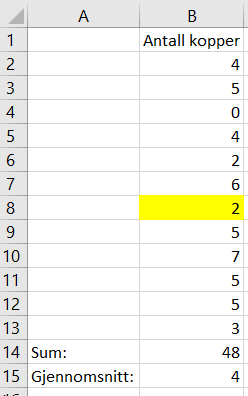
Bruker Excel til å beregne gjennomsnittet. Jeg kan da endre på tallet som var bak kaffeflekken, og se hvordan det påvirker gjennomsnittet.
Figuren viser at dersom vedkommende drikker 2 kopper kaffe blir gjennomsnittet akkurat 4.
Gjennomsnittet blir større enn 4 dersom tallet som skjuler seg bak flekken er 3 eller større.
Oppgave 3
Samlet vekstfaktor for vare A om tre måneder: $1,07^3 = 1,225$ det vil si at prisen vil være 22,5 % høyere om tre måneder enn den er nå.
Samlet vekstfaktor for vare B for tre måneder siden: $0,93^{-3} = 1,243$ det vil si at prisen var 24,3 % høyere for tre måneder siden enn den er nå.
Malins påstand er altså ikke riktig.
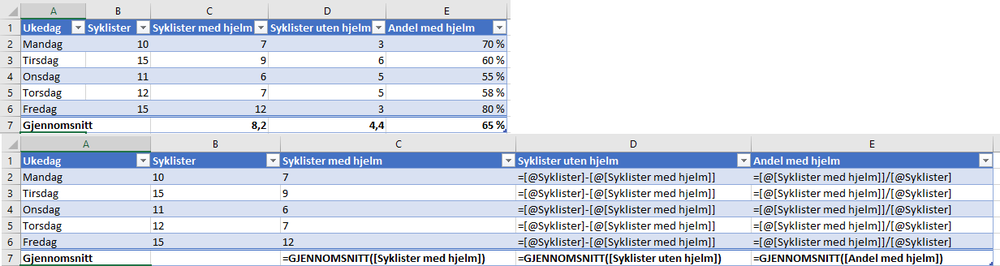
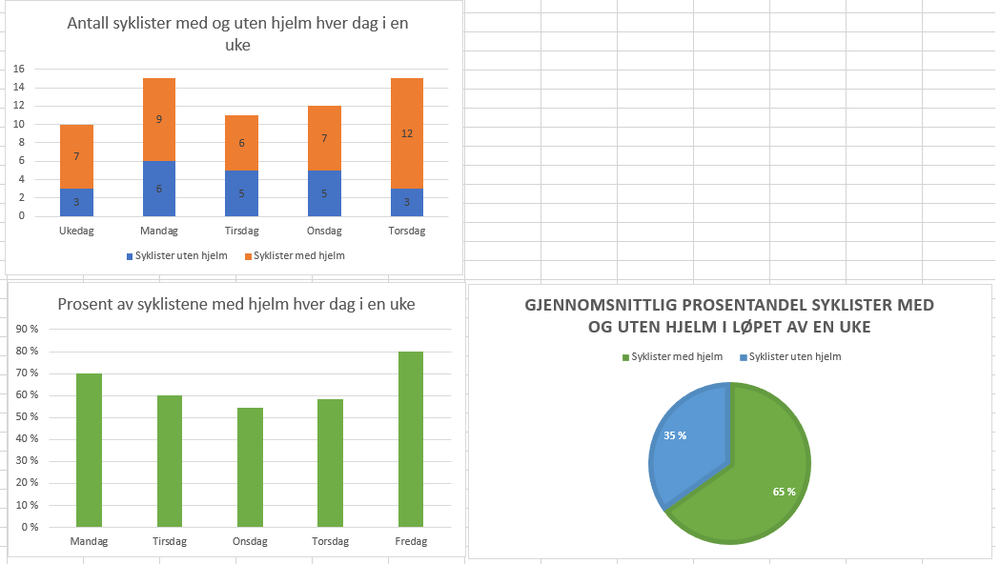
Oppgave 4
Oppgave 5
a)
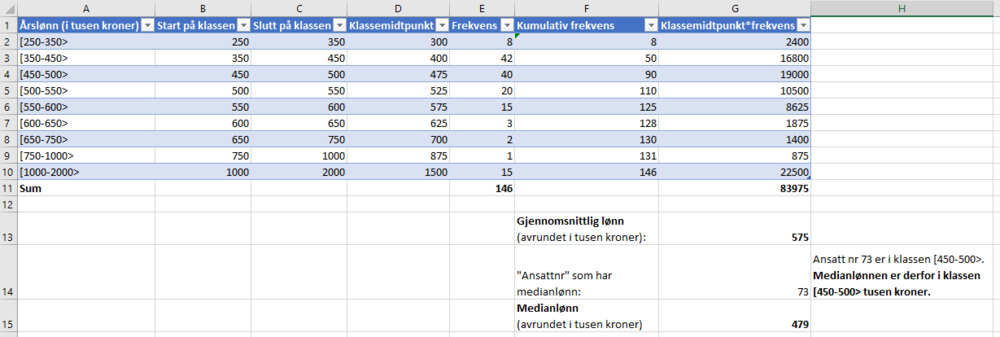
Bruker Excel til å beregne gjennomsnitt og median.
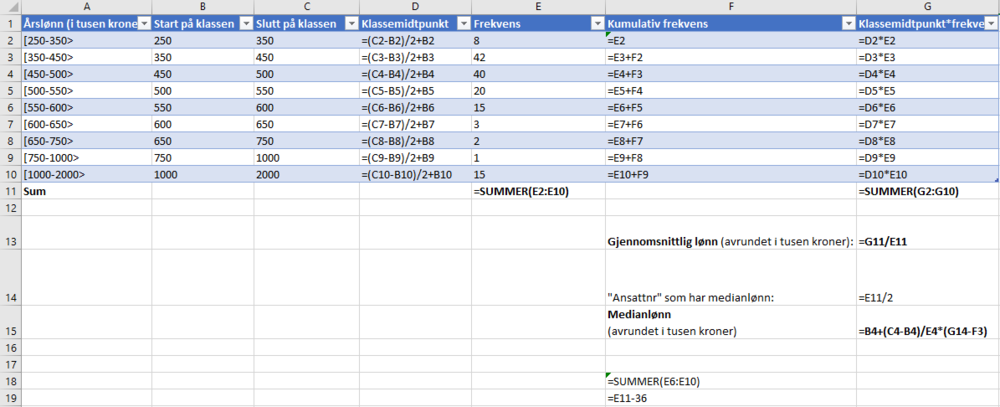
Med formler:
b)
Gjennomsnittslønnen er ca. 575 000 kr, mens medianlønnen er ca. 479 000 kr.
Gjennomsnittslønnen "dras opp" av de 15 ansatte med lønn over 1 million kr. Vi ser i tabellen at kun 36 ansatte har lønn over 550 000 kr, mens 110 ansatte har lønn under 550 000 kr. De vil si at de aller fleste har lønn under gjennomsnittet.
Medianlønnen forteller oss at halvparten av de ansatte har lønn under eller lik 479 000 kr. Sånn sett representerer medianlønnen de ansattes lønn best.