1P 2023 vår LK20 LØSNING: Forskjell mellom sideversjoner
| Linje 37: | Linje 37: | ||
===a)=== | ===a)=== | ||
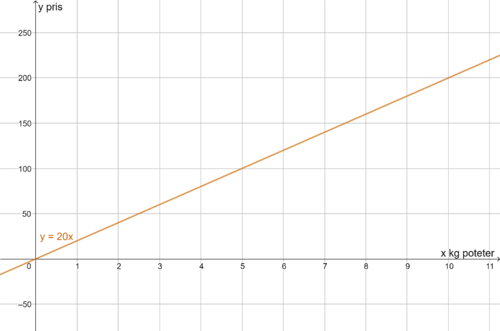
Prisen du må betale for poteter er proporsjonal med antall kg poteter du kjøper | Prisen du må betale for poteter er proporsjonal med antall kg poteter du kjøper. Vi antar at du kjøper poteter i løsvekt med en gitt kilopris, f.eks. 20 kr/kg. Kjøper du 1 kg, koster det 20 kr. Kjøper du 2 kg, koster det 40 kr. osv. | ||
Grunnen til at det er proporsjonale størrelser, er at forholdet mellom disse alltid er det samme (i dette tilfellet, at kiloprisen er lik). | Grunnen til at det er proporsjonale størrelser, er at forholdet mellom disse alltid er det samme (i dette tilfellet, at kiloprisen er lik). Vi har k = y/x. | ||
[[File: 1P-v23-del1-3a.png]] | [[File: 1P-v23-del1-3a.png|500px]] | ||
===b)=== | ===b)=== | ||
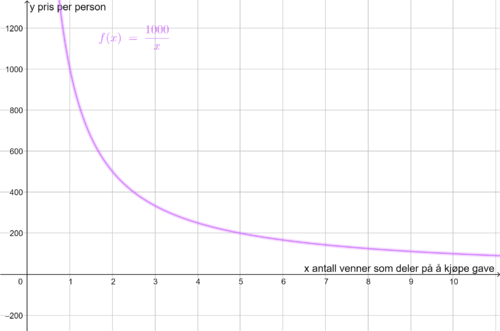
Prisen hver person må betale dersom en gruppe deler på å kjøpe gave til en venn, er omvendt proporsjonal med hvor mange personer som er med på å betale for gaven. Vi antar at gaven koster 1000 kr. Dersom bare 2 venner deler på prisen, må hver person betale 500 kr. Dersom 4 venner deler på prisen, må hver person betale 250 kr. osv. | |||
[[File: 1P-v23-del1-3b.png]] | Grunnen til at det er omvendt proporsjonale størrelser, er at produktet av disse alltid er det samme (i dette tilfellet, at prisen på gaven er fast). Vi har k = x*y. | ||
[[File: 1P-v23-del1-3b.png|500px]] | |||
=DEL 2= | =DEL 2= | ||
Sideversjonen fra 30. mai 2023 kl. 19:19
Diskusjon av oppgaven på matteprat
DEL 1
Oppgave 1
Det er 30 kr i prisforskjell mellom de to sjokoladeplatene.
Prisforskjell sammenlignet med prisen på butikken:
$\frac{30}{20}\cdot 100 \% = \frac{3}{2}\cdot 100\% = 1,5 \cdot 100 \% = 150 \%$
Sjokoladeplaten er 150 % dyrere på bensinstasjonen enn på butikken.
Prisforskjell sammenlignet med prisen på bensinstasjonen:
$\frac{30}{50}\cdot 100\% = \frac{60}{100}\cdot 100\% = 0,6\cdot 100\% = 60\% $
Sjokoladeplaten er 60 % billigere på butikken enn på bensinstasjonen.
Marko og Mari har regnet riktig. Den prosentvise prisforskjellen kommer an på hva man sammenligner prisforskjellen med.
Oppgave 2
8 milliarder på standardform: $8\cdot 10 ^9$
2,5 millioner på standardform: $2,5\cdot 10^6$
Antall maur på jorden: $8\cdot 10 ^9 \cdot 2,5\cdot 10^6 = 20 \cdot 10^{9+6} = 20 \cdot 10^{15} = 2 \cdot 10^{16}$
Det er omtrent $2 \cdot 10^{16}$ maur på jorden.
Oppgave 3
a)
Prisen du må betale for poteter er proporsjonal med antall kg poteter du kjøper. Vi antar at du kjøper poteter i løsvekt med en gitt kilopris, f.eks. 20 kr/kg. Kjøper du 1 kg, koster det 20 kr. Kjøper du 2 kg, koster det 40 kr. osv.
Grunnen til at det er proporsjonale størrelser, er at forholdet mellom disse alltid er det samme (i dette tilfellet, at kiloprisen er lik). Vi har k = y/x.
b)
Prisen hver person må betale dersom en gruppe deler på å kjøpe gave til en venn, er omvendt proporsjonal med hvor mange personer som er med på å betale for gaven. Vi antar at gaven koster 1000 kr. Dersom bare 2 venner deler på prisen, må hver person betale 500 kr. Dersom 4 venner deler på prisen, må hver person betale 250 kr. osv.
Grunnen til at det er omvendt proporsjonale størrelser, er at produktet av disse alltid er det samme (i dette tilfellet, at prisen på gaven er fast). Vi har k = x*y.
DEL 2
Oppgave 1
a)
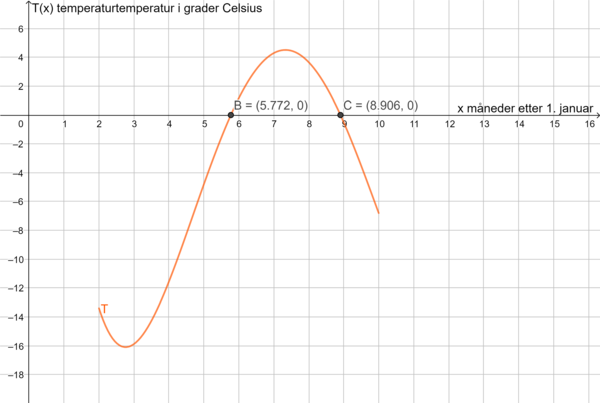
Bruker Geogebra til å tegne grafen til T, og finner de to nullpunktene i definisjonsområdet: B=(5.8,0) og C=(8.9,0).
Temperaturen er over 0 grader Celsius fra 5,8 til 8,9 måneder etter 1. januar.
Mai: måned nr. 5. I tillegg 0,8*31 = ca. 25 døgn inn i mai (6 døgn igjen av mai). August: måned nr. 8. I tillegg 0,9*31 = ca. 28 døgn inn i august.
Til sammen er temperaturen over 0 grader Celsius: 6 døgn i mai + 30 døgn i juni + 31 døgn i juli + 28 døgn i august = 95 døgn.
b)
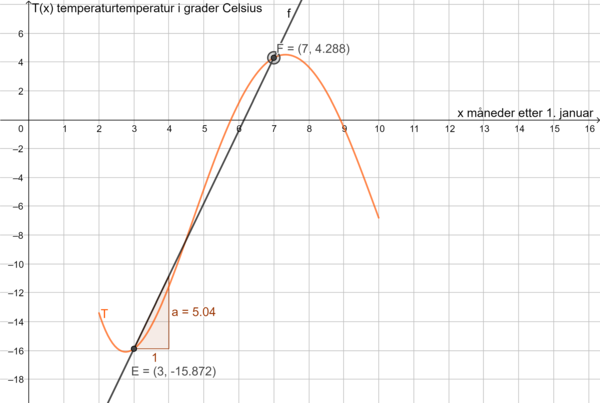
Lager punktene E=(3,T(3)) og F=(7,T(7)). Lager en linje mellom dem med knappen "linje", og finner stigningstallet til linjen med knappen "stigning".
Stigningstallet er 5.04, som betyr at temperaturen stiger med omtrent 5 grader Celsius per måned fra 1. mars til 1. juli.
Oppgave 3
a)
Dersom lengden er 60 meter, blir bredden 10 meter. Arealet blir da $60\cdot 10 = 600$ kvadratmeter.
b)
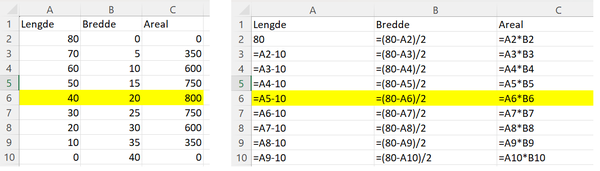
Bruker Excel til å lage en oversikt. Bildet viser oversikten til venstre, og formlene som er brukt til høyre.
Det kan se ut som om Herman sin påstand er riktig. I oversikten er det største arealet når lengden er dobbel så stor som bredden.
c)
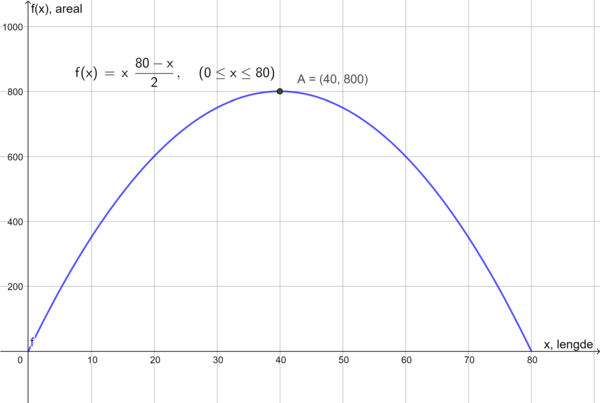
Funksjonen $f(x)=x\cdot \frac{80-x}{2}$ viser areal av rektangelet som funksjon av lengden x. Bruker Geogebra til å tegne grafen til f, og til å finne ekstremalpunktet A=(40,800).
Funksjonen viser at rektangelet har størst areal når lengden er 40, og da dobbelt så stor som bredden på 20.