1P 2023 vår LK20 LØSNING: Forskjell mellom sideversjoner
| Linje 4: | Linje 4: | ||
=DEL 1= | =DEL 1= | ||
==Oppgave 1== | |||
Det er 30 kr i prisforskjell mellom de to sjokoladeplatene. | |||
Prisforskjell sammenlignet med prisen på butikken: | |||
$\frac{30}{20}\cdot 100% = \frac{3}{2}\cdot 100% = 1,5 \cdot 100 % = 150 %$ | |||
Sjokoladeplaten er 150 % dyrere på bensinstasjonen enn på butikken. | |||
Prisforskjell sammenlignet med prisen på bensinstasjonen: | |||
$\frac{30}{50}\cdot 100% = \frac{60}{100}\cdot 100% = 0,6\cdot 100% = 60% $ | |||
Sjokoladeplaten er 60 % billigere på butikken enn på bensinstasjonen. Marko og Mari har regnet riktig. Den prosentvise prisforskjellen kommer an på hva man sammenligner prisforskjellen med. | |||
==Oppgave 2== | |||
=DEL 2= | =DEL 2= | ||
Sideversjonen fra 30. mai 2023 kl. 18:54
Diskusjon av oppgaven på matteprat
DEL 1
Oppgave 1
Det er 30 kr i prisforskjell mellom de to sjokoladeplatene.
Prisforskjell sammenlignet med prisen på butikken:
$\frac{30}{20}\cdot 100% = \frac{3}{2}\cdot 100% = 1,5 \cdot 100 % = 150 %$
Sjokoladeplaten er 150 % dyrere på bensinstasjonen enn på butikken.
Prisforskjell sammenlignet med prisen på bensinstasjonen:
$\frac{30}{50}\cdot 100% = \frac{60}{100}\cdot 100% = 0,6\cdot 100% = 60% $
Sjokoladeplaten er 60 % billigere på butikken enn på bensinstasjonen. Marko og Mari har regnet riktig. Den prosentvise prisforskjellen kommer an på hva man sammenligner prisforskjellen med.
Oppgave 2
DEL 2
Oppgave 1
a)
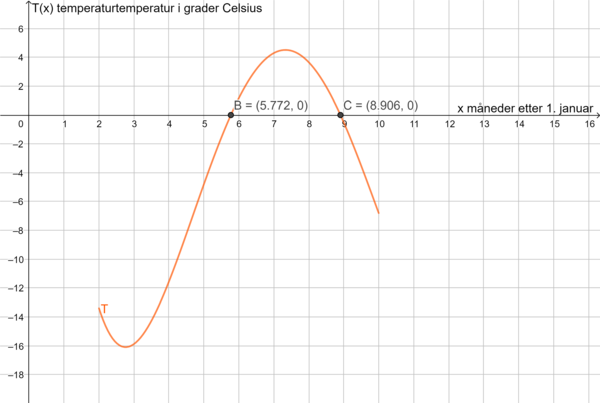
Bruker Geogebra til å tegne grafen til T, og finner de to nullpunktene i definisjonsområdet: B=(5.8,0) og C=(8.9,0).
Temperaturen er over 0 grader Celsius fra 5,8 til 8,9 måneder etter 1. januar.
Mai: måned nr. 5. I tillegg 0,8*31 = ca. 25 døgn inn i mai (6 døgn igjen av mai). August: måned nr. 8. I tillegg 0,9*31 = ca. 28 døgn inn i august.
Til sammen er temperaturen over 0 grader Celsius: 6 døgn i mai + 30 døgn i juni + 31 døgn i juli + 28 døgn i august = 95 døgn.
b)
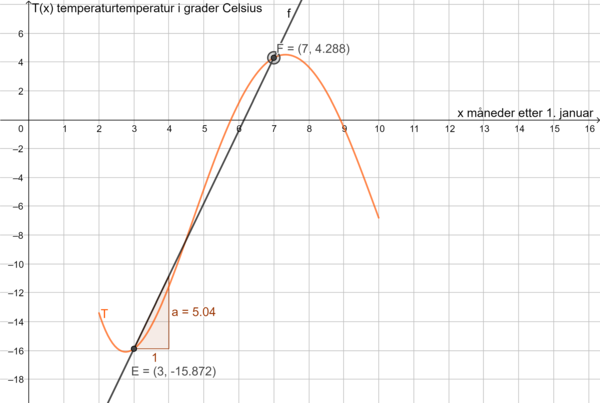
Lager punktene E=(3,T(3)) og F=(7,T(7)). Lager en linje mellom dem med knappen "linje", og finner stigningstallet til linjen med knappen "stigning".
Stigningstallet er 5.04, som betyr at temperaturen stiger med omtrent 5 grader Celsius per måned fra 1. mars til 1. juli.
Oppgave 3
a)
Dersom lengden er 60 meter, blir bredden 10 meter. Arealet blir da $60\cdot 10 = 600$ kvadratmeter.
b)
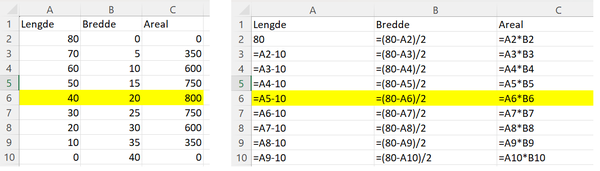
Bruker Excel til å lage en oversikt. Bildet viser oversikten til venstre, og formlene som er brukt til høyre.
Det kan se ut som om Herman sin påstand er riktig. I oversikten er det største arealet når lengden er dobbel så stor som bredden.
c)
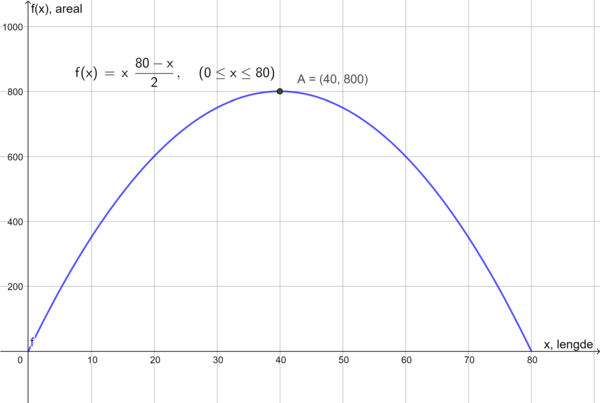
Funksjonen $f(x)=x\cdot \frac{80-x}{2}$ viser areal av rektangelet som funksjon av lengden x. Bruker Geogebra til å tegne grafen til f, og til å finne ekstremalpunktet A=(40,800).
Funksjonen viser at rektangelet har størst areal når lengden er 40, og da dobbelt så stor som bredden på 20.