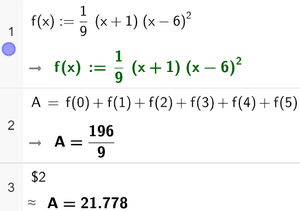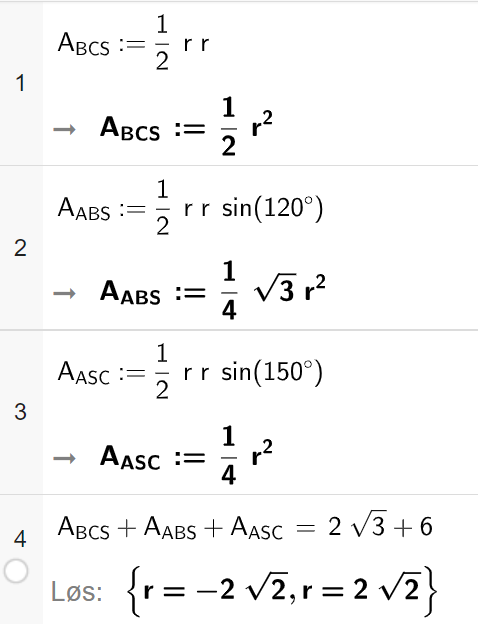1T 2023 vår LK20 LØSNING: Forskjell mellom sideversjoner
Fra Matematikk.net
| Linje 44: | Linje 44: | ||
==Oppgave 5== | ==Oppgave 5== | ||
Løser oppgaven i CAS. Finner arealet av hver trekant uttrykt ved r (linje 1-3), og løser til slutt likningen for summen av arealene til de tre trekantene (linje 4) for å finne verdien til r. | |||
Linje 1: vanlig formel for areal. | |||
Linje 2: arealsetningen. $\angle{ASB}= 180^{\circ}-30^{\circ}-30^{\circ} = 120^{\circ}$ | |||
Linje 3: arealsetningen. $\angle{ASC}= 360^{\circ}-90^{\circ}-120^{\circ} = 150^{\circ}$ | |||
[[File: 1T-v23-del2-5.png]] | |||
==Oppgave 6== | ==Oppgave 6== | ||
Sideversjonen fra 27. mai 2023 kl. 08:44
Diskusjon av oppgaven på matteprat
DEL 1
Oppgave 1
Oppgave 2
Oppgave 3
Oppgave 4
Oppgave 5
DEL 2
Oppgave 1
Oppgave 2
Oppgave 3
Oppgave 4
a)
Arealet av hvert rektangel er gitt ved:
$A=l\cdot b = 1\cdot f(x)$
Bruker CAS til å regne ut summen til arealet av de seks rektanglene.
Arealet er av de seks rektanglene er ca. 21,8.
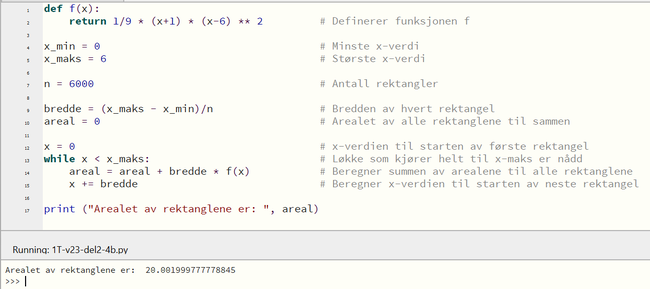
b) og c)
Arealet av 6000 rektangler er ca. 20.
Oppgave 5
Løser oppgaven i CAS. Finner arealet av hver trekant uttrykt ved r (linje 1-3), og løser til slutt likningen for summen av arealene til de tre trekantene (linje 4) for å finne verdien til r.
Linje 1: vanlig formel for areal.
Linje 2: arealsetningen. $\angle{ASB}= 180^{\circ}-30^{\circ}-30^{\circ} = 120^{\circ}$
Linje 3: arealsetningen. $\angle{ASC}= 360^{\circ}-90^{\circ}-120^{\circ} = 150^{\circ}$