Geometri I: Forskjell mellom sideversjoner
Ny side: xx |
Ingen redigeringsforklaring |
||
| Linje 1: | Linje 1: | ||
== Lengdemål == | |||
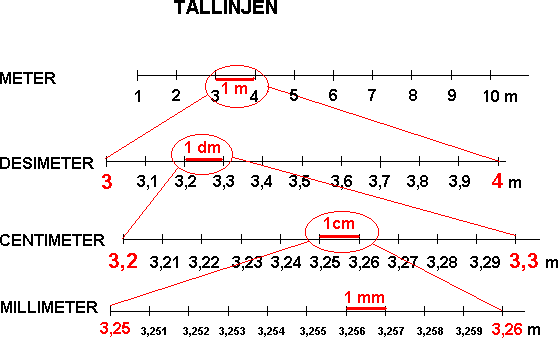
En lengde er gitt ved et måltall og en enhet. Enheten kalles for benevning. Eksempler på enheter er meter (m), desimeter (dm), centimeter (cm) og millimeter (mm). Vi har følgende sammenheng: 1m = 10dm = 100cm = 1000mm | |||
[[Bilde:Tallinjen_11.png]] | |||
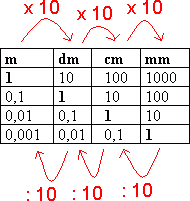
Skal man arbeide med flere lengder er det viktig at alle har samme enhet. Vi går fra en enhet til en mindre enhet ved å multiplisere måltallet med 10. Motsatt vei dividerer vi med 10. Ønsker man for eksempel å gå fra meter til centimeter må man multiplisere med 10 to ganger. | |||
[[Bilde:Line_11.png]] | |||
For større lengder har vi enhetene kilometer (km) og mil. 1km = 1000m = 0,1mil. 1 mil = 10km | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel'''<p></p> | |||
Hvor mange centimeter er 2,7 meter?<p></p> | |||
Man ganger med 10, to ganger og får:<p></p> | |||
<math> 2,7m \cdot 10 = 27dm \\ 27dm \cdot 10 = 270cm </math><p></p> | |||
Du kan selfølgelig gange med 100 en gang, det blir det samme som å gange med 10 to ganger. | |||
</blockquote> | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel'''<p></p> | |||
Hvor mange meter er 912 milimeter?<p></p> | |||
Du deler på 10 tre ganger (eller på 1000 en gang)<p></p> | |||
<math>912mm:10 = 91,2cm \\ 91,2cm: 10 = 9,12dm \\9,12dm:10=0,912m </math> | |||
</blockquote> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=A3E%2BA3F%2BA40%2BA41%2BA42%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
== Areal- flatemål == | |||
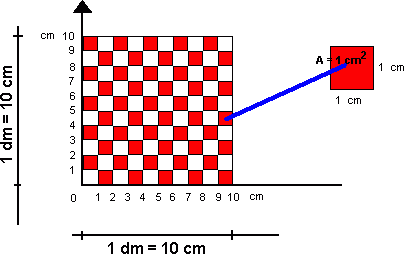
Et areal er gitt ved et måltall og en enhet. Enheten kalles for benevning. Eksempler på enheter er kvadratmeter <math> [m^2]</math> , kvadratdesimeter <math> [dm^2]</math>, kvadratcentimeter <math> [cm^2]</math> og kvadratmillimeter <math> [mm^2]</math>. Vi har følgende sammenheng: <math>1m^2 = 100dm^2 = 10000cm^2 = 1000000mm^2</math> | |||
[[Bilde:Areal_1.png]] | |||
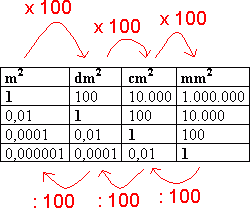
Skal man arbeide med flere areal er det viktig at alle har samme enhet. Vi går fra en enhet til en mindre enhet ved å multiplisere måltallet med 100. Motsatt vei dividerer vi med 100. Ønsker man for eksempel å gå fra kvadratmeter til kvadratcentimeter må man multiplisere med 100 to ganger. | |||
[[Bilde:Flate_tab_1.png]] | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel'''<p></p> | |||
Hvor mange kvadratcensimeter er 12 kvadratdesimeter?<p></p> | |||
Man ganger med hundre og får <math>1200cm^3</math> | |||
</blockquote> | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel'''<p></p> | |||
Hvor mange kvadratdesimeter er 54000 kvadratmilimeter?<p></p> | |||
Man deler på 100 to ganger og får<p></p> | |||
<math> 54000mm ^2:100 = 540cm^2 \\ 540cm^2:100 = 5,4 dm^2</math> | |||
</blockquote> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=A43%2BA44%2BA45%2BA46%2BA47%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
For større arealer har vi følgende enheter: <math>ar = 100 m^2, daa = dekar = 1 000 m^2, ha = hektar = 10 000 m^2, km^2 = kvadratkilometer = 1 000 000 m^2</math>. | |||
== Volum - rommål == | |||
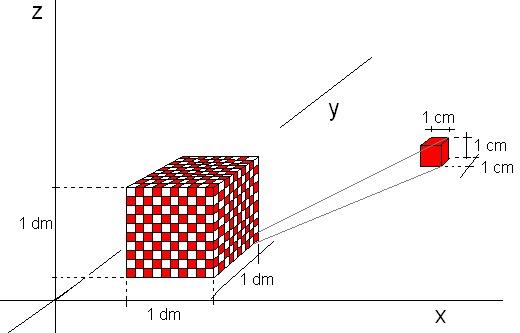
Et volum er gitt ved et måltall og en enhet. Enheten kalles for benevning. Eksempler på enheter er kubikkmeter <math> [m^3]</math> , kubikkdesimeter <math> [dm^3]</math>,kubikkcentimeter <math> [cm^3]</math> og kubikkmillimeter <math> [mm^3]</math>. Vi har følgende sammenheng: <math>1m^3 = 1000dm^3 = 1000000cm^3 = 1000000000mm^3</math> | |||
[[Bilde:Kube_1.PNG]] | |||
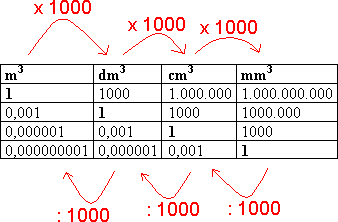
Skal man arbeide med flere volum er det viktig at alle har samme enhet. Vi går fra en enhet til en mindre enhet ved å multiplisere måltallet med 1000. Motsatt vei dividerer vi med 1000. Ønsker man for eksempel å gå fra kubikkmeter til kubikkcentimeter må man multiplisere med 1000 to ganger. | |||
[[Bilde:Vol_tab_1.png]] | |||
Når man regner ut et volum regner vi med en eller flere lengder. Når det arbeides med flere lengder må alle ha samme enhet. Se avsittet foran, om lengder. | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel'''<p></p> | |||
Hvor mange kubikkcentimeter er 0,26 kubikkmeter?<p></p> | |||
Man ganger med 1000 to ganger og får<p></p> | |||
<math>0,26m^3 \cdot 1000 = 260dm^3 \\ 260dm^3 \cdot 1000 = 260000 cm^3 | |||
</math> | |||
</blockquote> | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel'''<p></p> | |||
Hvor mange kubikkdesimeter er 12 kubikkcentimeter?<p></p> | |||
Man deler på 1000 og får<p></p> | |||
<math>12cm^3:1000= 0,012 dm^3</math> | |||
</blockquote> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=A48%2BA49%2BA4A%2BA4B%2BA4C%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
=== Fra kubikk til liter - og motsatt=== | |||
Du trenger kun å huske en ting:<p></p> | |||
1 liter = <math>1 dm^3</math>.<p></p> | |||
Nedenfor finer du en tabell som viser samenhengen.<p></p> | |||
<table border="1" cellpadding="10"> | |||
<tr> | |||
<td>'''hl '''</td> | |||
<td>'''l '''</td> | |||
<td>'''dl '''</td> | |||
<td>'''cl'''</td> | |||
<td>'''ml '''</td> | |||
<td>''' '''</td> | |||
<td>'''<math>m^3</math>'''</td> | |||
<td>'''<math>dm^3</math>'''</td> | |||
<td>'''<math>cm^3</math>'''</td> | |||
<td>'''<math> mm^3</math>'''</td> | |||
</tr> | |||
<tr> | |||
<td>'''1'''</td> | |||
<td>100</td> | |||
<td>1000</td> | |||
<td>10 000</td> | |||
<td>100 000</td> | |||
<td>''' '''</td> | |||
<td>0,1</td> | |||
<td>100</td> | |||
<td>100 000</td> | |||
<td> 100 000 000</td> | |||
</tr> | |||
<tr> | |||
<td>0,01</td> | |||
<td>'''1 '''</td> | |||
<td>10</td> | |||
<td>100</td> | |||
<td>1000</td> | |||
<td>''' '''</td> | |||
<td>0,001</td> | |||
<td>1</td> | |||
<td>1000</td> | |||
<td>1000 000</td> | |||
</tr> | |||
<tr> | |||
<td>0,001</td> | |||
<td>0,1</td> | |||
<td>'''1'''</td> | |||
<td>10</td> | |||
<td>100</td> | |||
<td>''' '''</td> | |||
<td>0,0001</td> | |||
<td>0,1</td> | |||
<td>100</td> | |||
<td>100 000</td> | |||
</tr> | |||
</table> | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel'''<p></p> | |||
En flaske inneholder 112 centiliter (cl) med saft. Hvor mange kubikkdesimeter er det?<p></p> | |||
112 cl er 1,12 liter som er 1,12<math>dm^3</math> | |||
</blockquote> | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel'''<p></p> | |||
Thor fyller bensintanken på mopeden med 7500 kubikkcentimeter bensin. Hvor mange liter er det? | |||
<p></p> <math> 7500cm^3=7,5dm^3=7,5l</math> | |||
</blockquote> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=B36%2BB37%2BB38%2BB39%2BB3A%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
---- | |||
[[Category:Geometri]] | |||
[[Category:U - trinn]] [[Category:1P]] [[Category:Ped]] | |||
Sideversjonen fra 31. mar. 2023 kl. 15:39
Lengdemål
En lengde er gitt ved et måltall og en enhet. Enheten kalles for benevning. Eksempler på enheter er meter (m), desimeter (dm), centimeter (cm) og millimeter (mm). Vi har følgende sammenheng: 1m = 10dm = 100cm = 1000mm
Skal man arbeide med flere lengder er det viktig at alle har samme enhet. Vi går fra en enhet til en mindre enhet ved å multiplisere måltallet med 10. Motsatt vei dividerer vi med 10. Ønsker man for eksempel å gå fra meter til centimeter må man multiplisere med 10 to ganger.
For større lengder har vi enhetene kilometer (km) og mil. 1km = 1000m = 0,1mil. 1 mil = 10km
Eksempel
Hvor mange centimeter er 2,7 meter?
Man ganger med 10, to ganger og får:
<math> 2,7m \cdot 10 = 27dm \\ 27dm \cdot 10 = 270cm </math>
Du kan selfølgelig gange med 100 en gang, det blir det samme som å gange med 10 to ganger.
Eksempel
Hvor mange meter er 912 milimeter?
Du deler på 10 tre ganger (eller på 1000 en gang)
<math>912mm:10 = 91,2cm \\ 91,2cm: 10 = 9,12dm \\9,12dm:10=0,912m </math>
Areal- flatemål
Et areal er gitt ved et måltall og en enhet. Enheten kalles for benevning. Eksempler på enheter er kvadratmeter <math> [m^2]</math> , kvadratdesimeter <math> [dm^2]</math>, kvadratcentimeter <math> [cm^2]</math> og kvadratmillimeter <math> [mm^2]</math>. Vi har følgende sammenheng: <math>1m^2 = 100dm^2 = 10000cm^2 = 1000000mm^2</math>
Skal man arbeide med flere areal er det viktig at alle har samme enhet. Vi går fra en enhet til en mindre enhet ved å multiplisere måltallet med 100. Motsatt vei dividerer vi med 100. Ønsker man for eksempel å gå fra kvadratmeter til kvadratcentimeter må man multiplisere med 100 to ganger.
Eksempel
Hvor mange kvadratcensimeter er 12 kvadratdesimeter?
Man ganger med hundre og får <math>1200cm^3</math>
Eksempel
Hvor mange kvadratdesimeter er 54000 kvadratmilimeter?
Man deler på 100 to ganger og får
<math> 54000mm ^2:100 = 540cm^2 \\ 540cm^2:100 = 5,4 dm^2</math>
For større arealer har vi følgende enheter: <math>ar = 100 m^2, daa = dekar = 1 000 m^2, ha = hektar = 10 000 m^2, km^2 = kvadratkilometer = 1 000 000 m^2</math>.
Volum - rommål
Et volum er gitt ved et måltall og en enhet. Enheten kalles for benevning. Eksempler på enheter er kubikkmeter <math> [m^3]</math> , kubikkdesimeter <math> [dm^3]</math>,kubikkcentimeter <math> [cm^3]</math> og kubikkmillimeter <math> [mm^3]</math>. Vi har følgende sammenheng: <math>1m^3 = 1000dm^3 = 1000000cm^3 = 1000000000mm^3</math>
Skal man arbeide med flere volum er det viktig at alle har samme enhet. Vi går fra en enhet til en mindre enhet ved å multiplisere måltallet med 1000. Motsatt vei dividerer vi med 1000. Ønsker man for eksempel å gå fra kubikkmeter til kubikkcentimeter må man multiplisere med 1000 to ganger.
Når man regner ut et volum regner vi med en eller flere lengder. Når det arbeides med flere lengder må alle ha samme enhet. Se avsittet foran, om lengder.
Eksempel
Hvor mange kubikkcentimeter er 0,26 kubikkmeter?
Man ganger med 1000 to ganger og får
<math>0,26m^3 \cdot 1000 = 260dm^3 \\ 260dm^3 \cdot 1000 = 260000 cm^3 </math>
Eksempel
Hvor mange kubikkdesimeter er 12 kubikkcentimeter?
Man deler på 1000 og får
<math>12cm^3:1000= 0,012 dm^3</math>
Fra kubikk til liter - og motsatt
Du trenger kun å huske en ting:
1 liter = <math>1 dm^3</math>.
Nedenfor finer du en tabell som viser samenhengen.
| hl | l | dl | cl | ml | <math>m^3</math> | <math>dm^3</math> | <math>cm^3</math> | <math> mm^3</math> | |
| 1 | 100 | 1000 | 10 000 | 100 000 | 0,1 | 100 | 100 000 | 100 000 000 | |
| 0,01 | 1 | 10 | 100 | 1000 | 0,001 | 1 | 1000 | 1000 000 | |
| 0,001 | 0,1 | 1 | 10 | 100 | 0,0001 | 0,1 | 100 | 100 000 |
Eksempel
En flaske inneholder 112 centiliter (cl) med saft. Hvor mange kubikkdesimeter er det?
112 cl er 1,12 liter som er 1,12<math>dm^3</math>
Eksempel
Thor fyller bensintanken på mopeden med 7500 kubikkcentimeter bensin. Hvor mange liter er det?
<math> 7500cm^3=7,5dm^3=7,5l</math>