Tall, tallmengder og intervaller: Forskjell mellom sideversjoner
| Linje 85: | Linje 85: | ||
==Tallmengder== | ==Tallmengder== | ||
$\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$ og $\mathbb{R}$ er eksempler på tallmengder. | $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$ og $\mathbb{R}$ er eksempler på tallmengder. | ||
En mengde består av en samling objekter. Vi sier at et objekt er et element i mengden. en mengde kan ha endelig eller uendelig antall elementer. | En mengde består av en samling objekter. Vi sier at et objekt er et element i mengden. en mengde kan ha endelig eller uendelig antall elementer. Dersom man skriver en mengde på listeform er det gjerne en endelig mengde. | ||
• | • Listeform: mengde utfall av et terningkast kan skrives slik {1,2,3,4,5,6}. | ||
• Mengden av de naturlige tallene, N, kan skrives N = {1,2,3,4,..} | • Mengden av de naturlige tallene, N, kan skrives N = {1,2,3,4,..} | ||
| Linje 134: | Linje 137: | ||
•Den vertikale streken: | leser vi "som er slik at"...Eks: | •Den vertikale streken: | leser vi "som er slik at"...Eks: | ||
{x R |2 ≤ x ≤ 10} = [2,10] | {x R |2 ≤ x ≤ 10} = [2,10] | ||
==Intervaller== | ==Intervaller== | ||
Sideversjonen fra 15. mar. 2023 kl. 11:54
Naturlige tall, - $\mathbb{N}$
De naturlige tallene er: 1, 2, 3, 4, 5, 6, 7, ............Vi kaller denne tallmengden for $\mathbb{N}$.
$\mathbb{N}$ er symbolet for de naturlige tallene, de positive heltallene: {1, 2, 3, ....}
Partall
Partallene er 2, 4, 6, 8....2n, der n er et naturlig tall forskjellig fra null.
Oddetall
Oddetallene er 1,3,5,7,9,11…….. Oddetallene er ikke delelige på to. Oddetall er en del av de naturlige tallene.
Dersom du lurer på om et tall kan deles på et annet kan du se på Delelighet.
Primtall
Primtall er naturlige tall som kun er delelige på seg selv og en. Legg merke till at 1 ikke er et primtall.
De minste primtallene er: 2,3,5,7,11,13,...................
Et naturlig tall som ikke er et primtall kaller vi et sammensatt tall. Sammensatte tall kan faktoriseres.
Primtall er en del av de naturlige tallene.
Hele tall, - $\mathbb{Z}$
Dersom vi tar alle de naturlige tallene inkluderer de hele negative tallene får vi en tallmengde vi kaller for $\mathbb{Z}$, som er de hele tallene.
$\mathbb{Z}$ ={ ...., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4,...} Alle hele tall, positive og negative, inkludert null.
Rasjonale tall, - $\mathbb{Q}$
En brøk er det vi kaller et rasjonalt tall. Et rasjonalt tall kan skrives som a/b. Alle rasjonale tall har enten en avsluttende desimal (teller delt på nevner har rest null etter et gitt antall desimaler), eller en periodisk desimalutvikling.
1/5 kan skrives som 0,2
2/3 kan skrives som 0,666666666666...........
4/11 kan skrives som 0,363636363636363636........
Det første eksempelet har en avsluttende desimal. Vi ser at i de to siste eksemplene gjentas sifrene i det uendelige. I tallet 0,666666... kan vi si at perioden er 6. I tallet 0,36363636 er perioden 36. Alle desimaltall som har en periode er rasjonale tall. Vi kaller de rasjonale tallene for $\mathbb{Q}$ .
Alle tall som kan skrives som brøk kalles rasjonale tall og har symbolet $\mathbb{Q}$
Reelle tall, - $\mathbb{R}$
Det finnes enkelte tall som ikke kan skrives som brøk. Et eksempel på det er tallet π (pi). Dersom du prøver å trykke det symbolet på kalkulatoren får du 3,141592654...... Det er ingen periode her, som det er i de rasjonale tallene. Vi kaller denne type tall for et irrasjonalt tall. De rasjonale og de irrasjonale tallene danner den tallmengden som vi kaller for de reelle tallene. Vi bruker symbolet $\mathbb{R}$ . $\mathbb{R}$ inneholder alle tallene på tallinja.
$\mathbb{R}$ er alle reelle tall, summen av rasjonale og irrasjonale tall, altså alle tall på tallinjen.
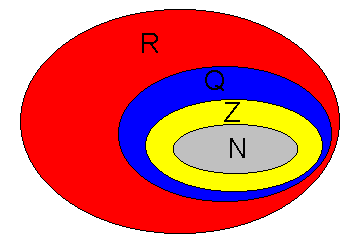
Figuren viser tallmengdene på tallinja. Legg merke til at $\mathbb{N}$ er en delmengde av $\mathbb{Z}$ og $\mathbb{Z}$ er igjen en delmengde av $\mathbb{Q}$ osv.
Tallmengder
$\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$ og $\mathbb{R}$ er eksempler på tallmengder. En mengde består av en samling objekter. Vi sier at et objekt er et element i mengden. en mengde kan ha endelig eller uendelig antall elementer. Dersom man skriver en mengde på listeform er det gjerne en endelig mengde.
• Listeform: mengde utfall av et terningkast kan skrives slik {1,2,3,4,5,6}.
• Mengden av de naturlige tallene, N, kan skrives N = {1,2,3,4,..}
• Symbolet Ø leses "den tomme mengden". Ø representerer en mengde uten elementer.
• De hele tallene Z kan skrives Z = {..-3,-2,-1, 0, 1, 2, 3..}
• Dersom to mengder skal trekkes fra hverandre brukes tegnet \. Tallmengden Z\N = {-1, -2, -3, -4,..}
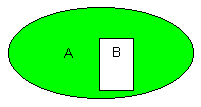
Det grønne feltet er mengden A\B.
• Dersom vi skal skrive opp alle tallene mellom 2 og 3 på tallinjen er det uendelig mange og klammeparentes duger ikke. Vi skriver intervallet av tall fra 2 til 3 som <2,3>. Dette kalles for et åpent intervall. Verken 2 eller 3 er med i tallmengden. Dersom vi skal skrive opp tallene fra og med 2 til og med 3 kan vi bruke et lukket intervall, [2,3].
• Ved å bruke skrivemåten over kan vi skrive mengden av alle tall fra og med null til uendelig som [0,→>. Vi bruker aldri en lukket klamme på uendelig.
• Dersom Stein er en elev i klasse 9b kan vi si at han er et element i klassen . Det kan vi skrive slik: <math>Stein \in 9b</math>.
•Jentene i 9b er en ekte delmengde av klassen,. det kan vi skrive slik:
<math>Jenter\quad \subset \quad 9b.</math>
Figuren over illustrerer at B er en ekte delmengde av A. <math>B \subset A</math>.
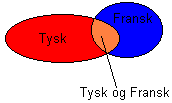
• De som har Tysk eller Fransk kan skrives slik: Tysk U Fransk. Tegnet leses union og kan forklares grafisk gjennom et Venn diagram:
• Mens union var de som hadde enten eller er snitt de som har både og (oransje): Tysk Fransk.
• De rasjonale tallene kalles Q. Et rasjonalt tall er av typen <math> \frac ab , \quad der \quad a,b \in Z</math>, og b forskjellig fra null.
• De reelle tallene betegnes R og omfatter alle tall på tallinjen.
•Den vertikale streken: | leser vi "som er slik at"...Eks:
{x R |2 ≤ x ≤ 10} = [2,10]
Intervaller
Et intervall er en mengde tall. Vi snakker om åpne og lukkede intervaller.
Lukket: $[a, b]$. Fra og med a til og med b.
Åpent:$\langle a,b \rangle$. Fra a til b, men ikke a og ikke b.
$[ 1,2 ]$ er et lukket intervall og omfatter alle de reelle tallene fra og med en, til og med to.
$\langle 1,2 \rangle$ er et åpent intervall og omfatter alle de reelle tallene fra en til to, men ikke en og to.
$[ 1,2 \rangle$ er et halvåpent intervall og omfatter alle de reelle tallene fra og med en, til to, men ikke to.
$\langle 1,2 ]$ er et halvåpent intervall og omfatter alle de reelle tallene som fra en, til og med to, men ikke en.
En alternativ skrivemåte er denne: A = { x ε R | 1 ≤ x ≤ 2}
Dette leses slik: " A består av alle x element i R som er slik at x er større eller lik en og mindre eller lik to", altså $[ 1,2 ]$