1T 2022 høst LK20 LØSNING

oppgaven som pdf

Diskusjon av oppgaven på matteprat

Oppgave 1

$tan\,u = \frac{motstående katet}{ hosliggende katet} = \frac 4 3$

$sin\,u = \frac{motstående katet}{ hypotenus} = \frac 4 5$

$cos\,u = \frac{ hosliggende katet}{ hypotenus} = \frac 3 5$

$ \frac{sin\,u}{ cos\,u} = \frac{\frac{4}{5}}{\frac{3}{5}} =\frac{4}{5}\cdot\frac{5}{3} = \frac{4}{3} $

$ \frac {sin\,u} {cos\,u} = tan\,u $

hvilket skulle vises.

Oppgave 2

a)

Nullpunktene til f(x) er x=-4, x=2 og x=4.

Disse nullpunktene passer best med graf A.

b)

Dette er samme uttrykk som f(x) i oppgave a). Vi ser av tegninga til graf A, at f(x)>0 i intervallene $x \in \langle -4,2 \rangle$ og $x \in \langle 4,\rightarrow \rangle$

Oppgave 3

a)

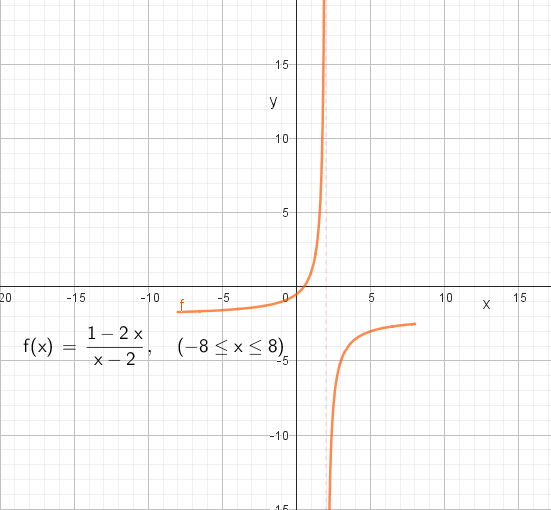
Programmet er trolig ment å skrive ut x verdier med tilhørende funksjonsverdi, fra 8 til -8. Det går bra helt til x=2, da prøver programmet å dele på null, og gir feilmelding. Hva Lars ønsker å bruke programmet til vet jeg ikke.

c)

Oppgave 4

Den deriverte til en parabel vil være en rett linje.

$f'(-2)= 9$ og $f'(8) =-11$, Dette er punkter på grafen til den deriverte.

Vi er på jakt etter likningen y = ax + b og finner først a:

$a= \frac{\Delta y}{\Delta x} = \frac{y_2 -y_1}{x_2 - x_1} = \frac{-11-9}{8 - (-2)} = -2$

$y = -2x + b$

Så kan vi bruke punktet( 8, -11) og får

$-11 = -2 \cdot 8 + b$ gir b = 5

Desom vi bruker det andre punktet: $9 = -2 \cdot (-2) +b$ gir også b = 5.

Likningen til den deriverte blir y = -2x + 5

Oppgave 1

a)

Da er x null, så temperaturen blir da 3,5 + 34,5 = 38 grader celsius når strømmen slåes av.

d)

Den mest ekstreme momentane endringen er i starten, rett etter at strømmen blir slått av. Da er endringen - 4,8

e)

3,5 er temperaturen til omgivelsene.

Oppgave 2

Antalls treroms er x og antall toroms er y.

x + y = 40

3x+ 2y = 90

Multipliserer første likning med -2. Legger så sammen likningene og får

x = 10. Da er y= 30.

Det er altså 10 treroms og 30 toroms i bygården.