Statistikkutkast

Utvalg

Dersom man produserer 1000 enheter av noe per dag og ønsker å sjekke kvaliteten kan det være for tidkrevende å sjekke alle 1000. Vi han ta et tilfeldig utvalg, en stikkprøve, og ved å få informasjon om utvalget kan vi forhåpentligvis si litt om hele produksjonen. Når man analyser tallmaterialet kan man selvsagt gjøre det for hånd, men det er tidkrevende og digitale hjelpemidler er gode på dette. Fordelen med å bruke regneark eller programmering er at du trolig vil treffe disse igjen etter vgs. Du kan også bruke Geogebra, men det er ikke sikkert du støter på dette programmet etter vgs.

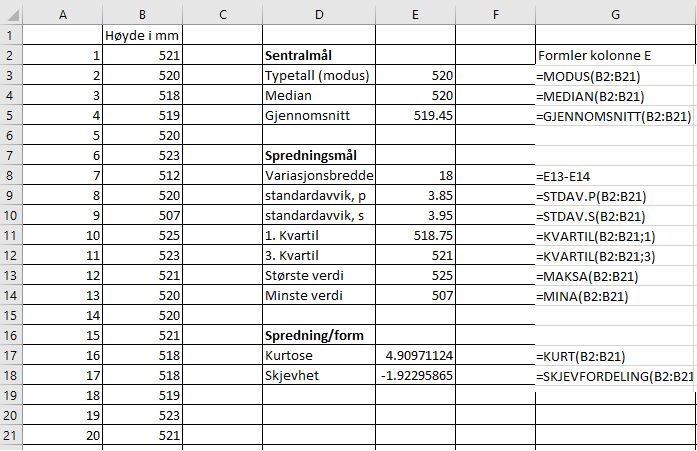
Nedenfor viser regnearket 20 tilfeldige verdier fra en produksjon på 1000. Vi ønsker å bruke de 20 enhetene til å si noe om hele dagsproduksjonen på 1000. 1000 er da populasjonen og 20 er utvalget ("sampel" på engelsk)

Her har vi tatt et utvalg på 20 fra en produksjonsserie på 1000. Vi har målt høyden på det enkelte produkt.

Kurtose. Normalfordelingen har kurtose 3. Høyere tall indikerer større forekomst av ekstreme verdier og motsatt.

Skjevhet. Dersom skjevheten er null er fordelingen symmetrisk

[ https://matematikk.net/side/Spredningsm%C3%A5l | Spredningsmål ]

Standardnormalfordelingen

En stokastisk variabel X med forventning $\mu =10 $ og standardavvik $\sigma = 3$ kan standardiseres ved variabelen Z.

$Z = \frac{X - \mu}{\sigma}$

Z er normalfordelt med forventning = og standardavvik 1. Z er standardnormalfordelt.