1P 2021 høst LK20 LØSNING: Forskjell mellom sideversjoner
| Linje 111: | Linje 111: | ||
===d)=== | ===d)=== | ||
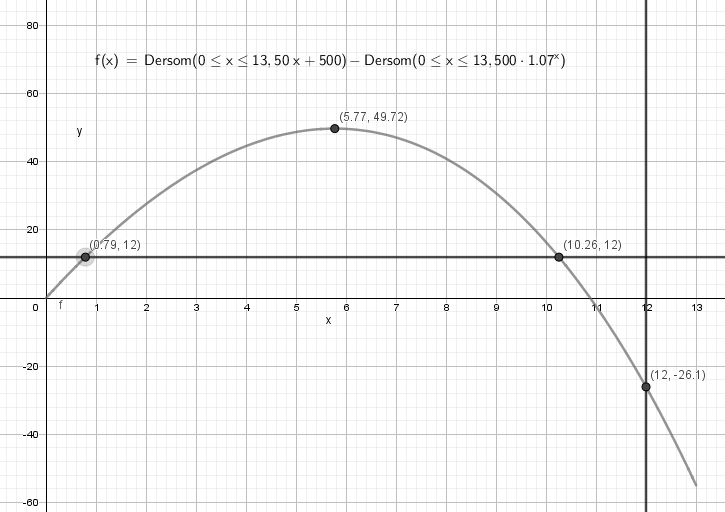
Grafen til f viser forskjellen i estimat mellom den lineære modellen og den eksponentielle, under de gitte forutsetninger. Den største forskjellen er på ca. 50 dyr, etter ca 6 år. Den praktiske tolkningen av y= 12 er ved hvilke tidspunkt den lineære modellen estimerer 12 dyr mer enn den eksponentielle. For x = 12 får vi en funksjonsverdi | Grafen til f viser forskjellen i estimat mellom den lineære modellen og den eksponentielle, under de gitte forutsetninger. Den største forskjellen er på ca. 50 dyr, etter ca 6 år. Den praktiske tolkningen av y= 12 er ved hvilke tidspunkt den lineære modellen estimerer 12 dyr mer enn den eksponentielle. For x = 12 får vi en funksjonsverdi nær - 26. Det må tolkes som at den eksponentielle funksjonen nå har det høyeste estimatet og etter 12 år er det ca 26 dyr. | ||
==Oppgave 4== | ==Oppgave 4== | ||
Sideversjonen fra 27. nov. 2021 kl. 13:42
DEL EN
Oppgave 1
Det betyr at 5 elever utgjør 20%, Da er 25 elever 100%.
Oppgave 2
Grunnlaget man regner prosenten fra forandrer seg hvert år. Du kan sette opp stykket slik:
$x \cdot 0,90^3 = 400 000 $
$x = 400 000 \cdot 0,90^{-3} $
Oppgave 3
a)
$T = 9t + 7$
$52 = 9 t + 7$
$9t = 45$
$t = 5$
Det tar ca. fem timer.
b)
7 er starttemperaturen ved tiden t = 0. 9 er antall grader temperaturen stiger med hver time.
Oppgave 4
Han bruker 9 minutter på første delen og 12 minutter på siste halvdel, totalt 21 minutter:
$\frac{12}{80} timer \cdot 60 + \frac {12}{60} timer \cdot 60 = 9 + 12 $ minutter
Oppgave 5
a)
f(x) vi ser at grafen krysser y aksen i 3 og at stigningstallet er -2 (to til høyre og fire ned). Det gir f(x) = -2x + 3
g(x) = 1/2 x - 2 ( stigningstall: to til høyre og en opp (delta y delt på delta x)
b)
Høyden i trekanten er 1. Grunnlinjen er : g(x)=0 gir x = 4, og f(x)= 0 gir x = 1,5. Grunnlinjen G= 4 - 1,5 = 2,5. Arealet blir halvparten av G*h som er 1,25.
DEL TO
Oppgave 1
a)
b)
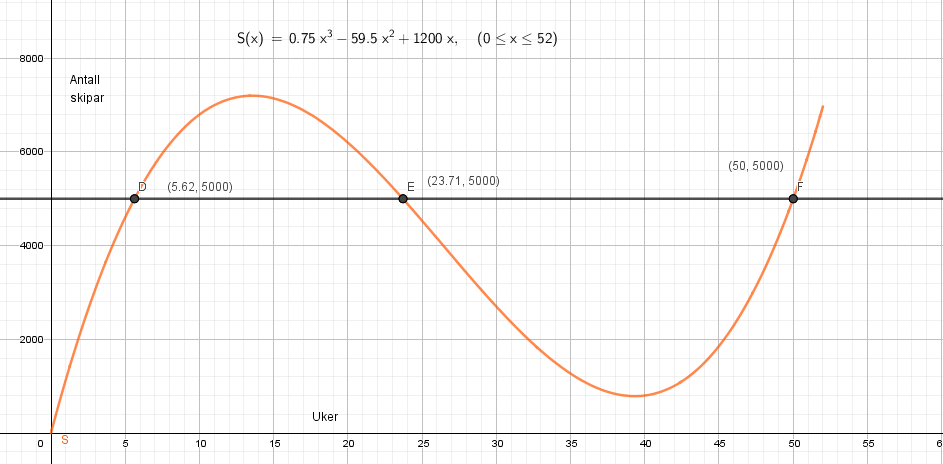
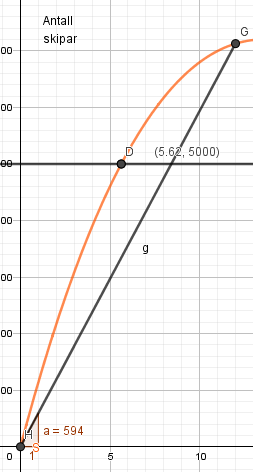
Stigningstallet er 594, det betyr at i årets første 12 uker øker skisalget i gjennomsnitt med ca. 600 par i uken.
Oppgave 2
a)
Energiinnhold i 100 gram kokt egg:
Energi fra fett + energi fra protein + energi fra karbohydrater = $(9 \cdot 10,2 + 4 \cdot 12,4 + 4 \cdot 0,3) kcal = 142,6 kcal$
b)
Gram spiselig: $125g \cdot 0,88 = 110g $
Energi: $1,1 \cdot 142,6 = 156 kcal $
Hvilket utgjør ca 5 % av dagsbehovet.
Oppgave 3
a)
Dersom en bestand bestående av 500 dyr dobler seg lineært på 10 år ser funksjonen slik ut: L(x) = 50 x + 500
b)
Dersom bestanden øker eksponentielt får vi:
$E(x)= 500 \cdot 1,07^x$
c)
d)
Grafen til f viser forskjellen i estimat mellom den lineære modellen og den eksponentielle, under de gitte forutsetninger. Den største forskjellen er på ca. 50 dyr, etter ca 6 år. Den praktiske tolkningen av y= 12 er ved hvilke tidspunkt den lineære modellen estimerer 12 dyr mer enn den eksponentielle. For x = 12 får vi en funksjonsverdi nær - 26. Det må tolkes som at den eksponentielle funksjonen nå har det høyeste estimatet og etter 12 år er det ca 26 dyr.
Oppgave 4
Påstand 1 er riktig: $pris per elev =\frac{totalutgift}{Antallelever}$
Påstand 2 er feil:
Oppgave 5
Saftblandingen består av 1 del sukker og ni deler ikke sukker. Dersom mengden sukker økes med 50% betyr det at vi har 1,5 del sukker og 9 deler ikke sukker. Det er totalt 10,5 deler. $\frac{1,5}{10,5} = 14,3$. Den nye blandingen vil inneholde i overkant av 14% sukker.
Oppgave 6
a)
b)
c)
Oppgave 7
a)
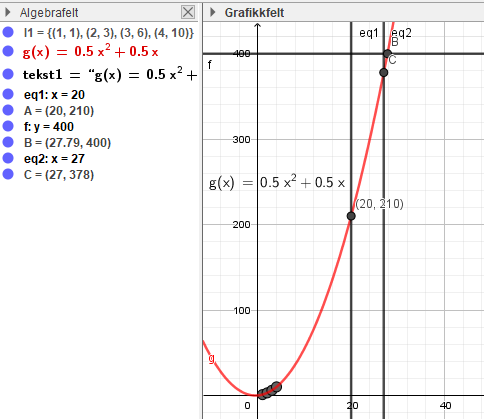
Finner funksjonsuttrykket ved regresjon i Geogebra. Ser at 20 etasjer krever 210 bokser.
b)
Han kan lage 27 etasjer. Til det trenger han 378 bokser. Se figur i a.
c)
d)
Oppgave 8
a)
Tallene er organisert i et kvadrat med tall fra 1 til 100, ti bortover og ti nedover. Et tilfeldig valgt tall n som ikke ligger på randen av det store kvadratet vil ha naboen n+1 til høyre for seg, og n-1 til venstre. Rett ned ligger n + 10 og rett opp n-10.
differansen en opp og en til høyre blir 11 - 2 = 9 (blått kvadrat) eller 37 - 28 = 9 (rød kvadrat). Den andre diagonalen får verdi 11 og produktet av 11 og 9 er 99, samme for både blått og rødt kvadrat.
b)
Uansett valg av 2 x 2 kvadrat blir produktet 99. Årsaken er at det kvadratet du velger har tallene : ![]() Differansen i diagonalen opp mot høyre vil være (n + 10) - (n + 1) = 10- 1 = 9 . Den andre diagonalen får differanse (n + 10 + 1) - n = 11
Differansen i diagonalen opp mot høyre vil være (n + 10) - (n + 1) = 10- 1 = 9 . Den andre diagonalen får differanse (n + 10 + 1) - n = 11
c)
Ett 3 x 3 kvadrat har alltid verdiene 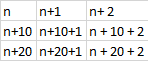 Produktet vil alltid være $18 \cdot 22$
Produktet vil alltid være $18 \cdot 22$