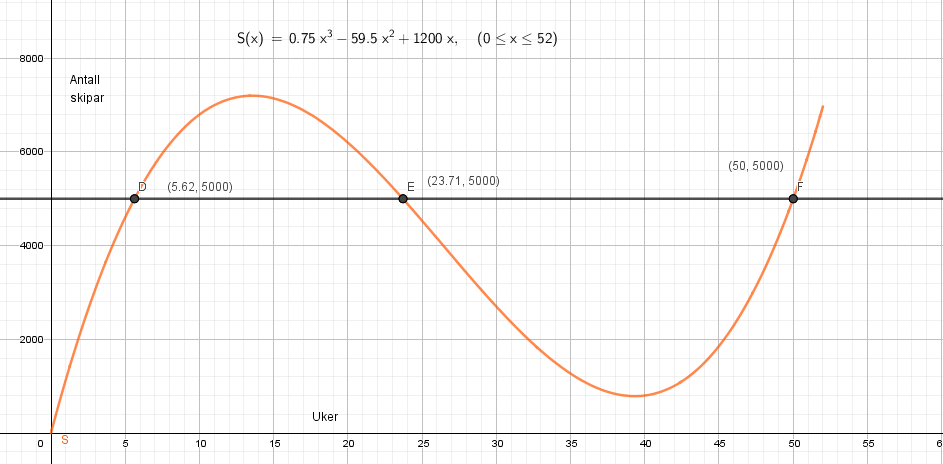
1P 2021 høst LK20 LØSNING: Forskjell mellom sideversjoner
| Linje 66: | Linje 66: | ||
===b)=== | ===b)=== | ||
[[File: 241121-02.png]] | |||
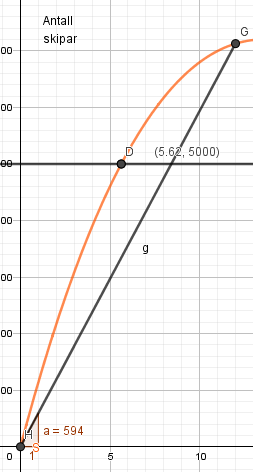
Stigningstallet er 594, det betyr at i årets første 12 uker øker skisalget i gjennomsnitt med ca. 600 par i uken. | |||
==Oppgave 7== | ==Oppgave 7== | ||
==Oppgave 8== | ==Oppgave 8== | ||
Sideversjonen fra 24. nov. 2021 kl. 10:15
DEL EN
Oppgave 1
Det betyr at 5 elever utgjør 20%, Da er 25 elever 100%.
Oppgave 2
I perioden har hun hatt en lønnsøkning på 12%. KPI var 12,2%, altså har hun hatt en nedgang i kjøpekraft.
Grunnlaget man regner prosenten fra forandrer seg hvert år. Du kan sette opp stykket slik:
$x \cdot 0,90^3 = 400 000 $
$x = 400 000 \cdot 0,90^{-3} $
Oppgave 3
Målestokk 5 : 1 er en forstørrelse av virkeligheten. Delen skal være $ \frac{5}{1} = \frac{140}{x}$. Dvs. x = 28 mm lang.
a)
$T = 9t + 7$
$52 = 9 t + 7$
$9t = 45$
$t = 5$
Det tar ca. fem timer.
b)
7 er starttemperaturen ved tiden t = 0. 9 er antall grader temperaturen stiger med hver time.
Oppgave 4
Han bruker 9 minutter på første delen og 12 minutter på siste halvdel, totalt 21 minutter:
$\frac{12}{80} timer \cdot 60 + \frac {12}{60} timer \cdot 60 = 9 + 12 $ minutter
Oppgave 5
a)
f(x) vi ser at grafen krysser y aksen i 3 og at stigningstallet er -2 (to til høyre og fire ned). Det gir f(x) = -2x + 3
g(x) = 1/2 x - 2 ( stigningstall: to til høyre og en opp (delta y delt på delta x)
b)
Høyden i trekanten er 1. Grunnlinjen er : g(x)=0 gir x = 4, og f(x)= 0 gir x = 1,5. Grunnlinjen G= 4 - 1,5 = 2,5. Arealet blir halvparten av G*h som er 1,25.
DEL TO
Oppgave 1
a)
b)
Stigningstallet er 594, det betyr at i årets første 12 uker øker skisalget i gjennomsnitt med ca. 600 par i uken.