S1 2009 høst LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| Linje 1: | Linje 1: | ||
Løsning laget av Svein Arneson: [pdf https://www.matematikk.net/matteprat/download/file.php?id=3363] [word https://www.matematikk.net/matteprat/download/file.php?id=3362] | |||
==Oppgave 1:== | ==Oppgave 1:== | ||
Sideversjonen fra 15. feb. 2021 kl. 12:21
Løsning laget av Svein Arneson: [pdf https://www.matematikk.net/matteprat/download/file.php?id=3363] [word https://www.matematikk.net/matteprat/download/file.php?id=3362]
Oppgave 1:
a)
1)
$5a^2+(a-2)(a+2)-(2a+1)=5a^2+a^2-4-2a-1=6a^2-2a-5$
2)
$\frac{2(x-2)}{3x}+\frac{1}{2}=\frac{2}{2}\cdot\frac{2x-4}{3x}+\frac{3x}{6x}=\frac{7x-8}{6x}=\frac{7}{6}-\frac{4}{3x}$
3)
$\frac{a^4 \cdot 2b^2}{(2a)^3}=\frac{a^4\cdot2b^2}{2^3\cdot a^3}=\frac{ab^2}{4}$
4)
$lg(a^2b)-lg(\frac{1}{ab})=2lga+lgb-(lg1-lga-lgb)=2lga+lgb-lg1+lga+lgb=3lga+2lgb=lg(a^3b^2)$
b)
1)
$\frac{x}{4}-\frac{1}{6}=\frac{x}{6}-(\frac{x}{2}-1)=>\frac{x}{4}-\frac{x}{6}+\frac{x}{2}=1+\frac{1}{6}$
$x(\frac{1}{4}-\frac{1}{6}+\frac{1}{2})=x\cdot \frac{7}{12}=\frac{7}{6}=>x=2$
2)
$2x^2-2(x+2)=20=>2x^2-2x-24=0$
$2(x^2-x-12)=0=>2(x-4)(x+3)=0=>x=4 \vee x=-3$
c)
masse til skrue målt i gram: s. masse til mutter målt i gram:m
$3s+2m=57$
$ s+3m=33|\cdot3=>3s+9m=99$
$3s+9m-(3s+2m)=99-57=42=>7m=42=>m=6=>s=33-3\cdot6=15$
En skrue veier 15 gram og en mutter veier 6 gram.
d)
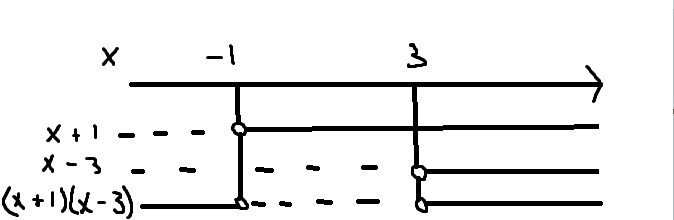
$x^2-2x \leq 3=>x^2-2x-3=(x+1)(x-3)\leq0$
$ x\in[-1,3]$
Oppgave 2:
a)
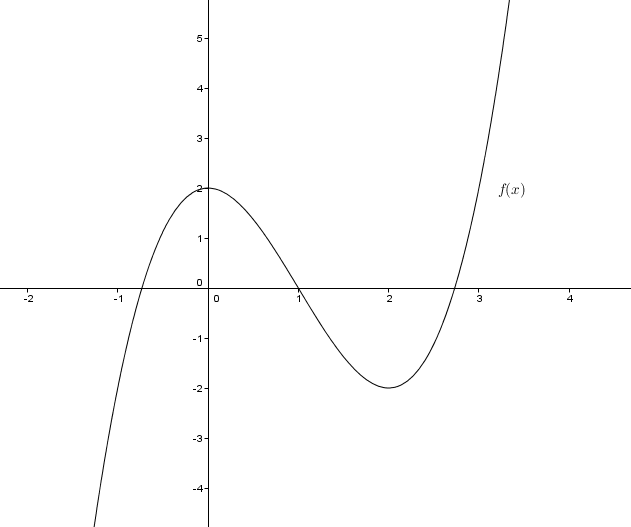
$f(x)=x^3-3x^2+2$
$f(-1)=-1-3+2=-2$
$f(0)=2$
$f(1)=1-3+2=0$
$f(2)=8-12+2=-2$
$f(3)=27-27+2=2$
b)
$f(x)=x^3-3x^2+2=>f'(x)=3x^2-6x=3x(x-2)$
Ekstremalpunkter:
$f'(x)=3x(x-2)=0=>x=0 \vee x=2$
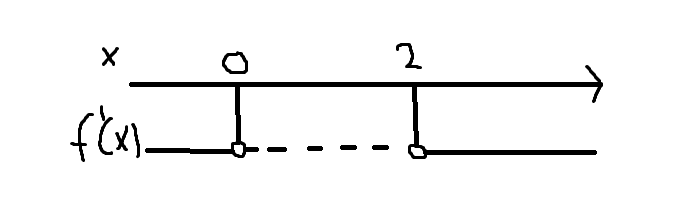
Toppunkt: $(0,f(0))=(0,2)$
Bunnpunkt: $(2,f(2))=(2,-2)$
c)
d)
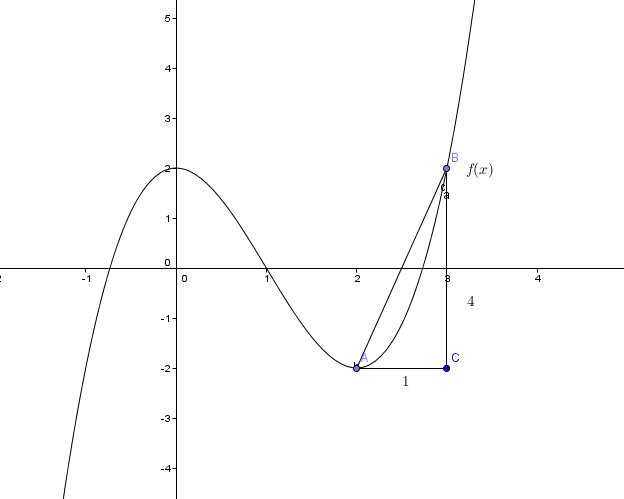
Ved regning:
$\frac{f(3)-f(2)}{3-2}=2-(-2)=4 $
Grafisk:
Oppgave 3:
a)
$10^{2x}-10^x-6=0=>(10^x)^2-10^x-6=0$
Bruker ABC-formelen.
$10^x=-2 \vee 10^x=3=>x=lg3$
$(10^x=-2$ har ingen løsning.)
b)
$lg(2x-2)-lg(x+5)=0=>lg(2x-2)=lg(x+5)$
$2x-2=x+5=>x=7$