1P 2020 høst LØSNING

oppgaven som pdf

Diskusjon av denne oppgaven på matteprat

Løsning laget av LektorNilsen

Videoløsning del 1 laget av Lektor Lainz

DEL 1

Oppgave 1

Leser av punktet (0,5000) og (5,7000). Finner stigningstallet til linjen, som også er prisen per kjøretime:

$a=\frac{y_2-y_1}{x_2-x_1} = \frac{7000-5000}{5-0}=\frac{2000}{5}=400$

Erik må betale 400 kr for hver kjøretime.

Oppgave 2

Antall deler: $5+7=12$

Antall elever per del: $\frac{24}{12}=2$

Antall jenter i klassen: $5\cdot 2 = 10$

Det er 10 jenter i klassen.

Oppgave 3

a)

Det er 1 L, det vil si 10 dL, filterkaffe på 8 kopper.

Antall desiliter filterkaffe per kopp: $\frac{10}{8} = \frac{5}{4} = 1,25$

Det vil bli 1,25 dL filterkaffe per kopp.

b)

Bruker forholdsregning. Det er 6 strøkne måleskjeer for 1 L filterkaffe, og x strøkne måleskjeer for 1,5 L filterkaffe. Vi antar at forholdet mellom antall strøkne kaffeskjeer og antall liter filterkaffe skal være det samme.

$\frac{x}{1,5}=\frac{6}{1} \\ x = 6\cdot 1,5 \\ x=9$

Kaffekalkulatoren vil beregne 9 strøkne måleskjeer til 1,5 L filterkaffe.

Oppgave 4

a)

Sidene i kvadratet har sidelengde 2s. Trekanten CED er likebeint, der CE = DE. Vi har fra figuren at $\angle EFC = 90^{\circ}$. Punkt F er derfor midtpunktet i DC, og DF = FC = s.

Trekanten FCE har en vinkel på 90 grader og en vinkel på 45 grader. Den siste vinkelen, $\angle CEF$, må derfor være $180-90-45 = 45$ grader. Trekant FCE har to like store vinkler, og er derfor likebeint. Vi har $EF= FC= s$.

Areal av trekanten CED: $A=\frac{g\cdot h}{2}=\frac{DC\cdot EF}{2}=\frac{2s\cdot s}{2} = s^2$

Areal av kvadratet ABCD: $A= 2s\cdot 2s = 4s^2$

Areal av figuren totalt: $A=s^2+4s^2 = 5s^2$, som skulle vises.

b)

Arealet av trekant CED skal være $36 cm^2$.

$s^2=36 \\ s= \sqrt{36} \\ s = 6$

Sidelengden i kvadratet er 2s. $2s = 2\cdot 6 = 12$

Sidelengden i kvadratet må være 12 cm.

Oppgave 5

a)

$P(\overline{C} \cap \overline{G})=P(\overline{C})\cdot P(\overline{G})= \frac{8}{10}\cdot \frac{7}{9}=\frac{56}{90}=\frac{28}{45}$

Sannsynligheten for at verken Charlotte eller Gunnar blir trukket ut er $\frac{28}{45}$

b)

$P(C \cap G) = P(C)\cdot P(G) = \frac{2}{10} \cdot \frac{1}{9} = \frac{2}{90} = \frac{1}{45}$

Sannsynligheten for at det blir Charlotte og Gunnar som skal lage kampoppsettet er $\frac{1}{45}$

Oppgave 6

a)

Trekant ABC er rettvinklet. Bruker Pytagorassetningen for å finne lengden BC.

$AC^2+BC^2=AB^2 \\ 6^2+BC^2=10^2 \\ BC^2 = 100-36 \\ BC = \sqrt{64} \\ BC = 8$

BC = 8 m.

b)

$\angle CDB = 180^{\circ}-90^{\circ}=90^{\circ}$.

Trekant ABC og trekant BCD har en felles vinkel, $\angle B$.

Trekant ABC og trekant BCD har begge en 90 graders vinkel.

Dersom to trekanter har to parvis like store vinkler, er disse trekantene formlike. Trekant ABC og trekant BCD er derfor formlike.

c)

Bruker forholdet ved formlikheten til trekantene ABC og BCD, til å regne ut høyden CD.

$\frac{CD}{BC}=\frac{AC}{AB} \\ \frac{CD}{8}=\frac{6}{10} \\ CD = \frac{6\cdot 8}{10} \\ CD = 4,8 $

CD = 4,8 m.

Oppgave 7

a)

5% av menn i yrkesaktiv alder er ikke i stand til å arbeide på grunn av uførhet.

b)

13 + 2 = 15

Det er 15 prosentpoeng i forskjell mellom personer med kun grunnskoleutdanning og personer med høyere utdanning i yrkesaktiv alder som ikke er i stand til å arbeide på grunn av uførhet.

c)

5 + 9 = 14

Det er 14 prosentpoeng i forskjell mellom menn og kvinner i yrkesaktiv alder som ikke er i stand til å arbeide på grunn av uførhet. Deler forskjellen i prosentpoeng på prosent menn som ikke er i stand til å arbeide på grunn av uførhet:

$\frac{14}{5} = \frac{28}{10} = \frac{280}{100} = 280$ %

Det er 280% flere kvinner enn menn i yrkesaktiv alder som ikke er i stand til å arbeide på grunn av uførhet.

DEL 2

Oppgave 1

a)

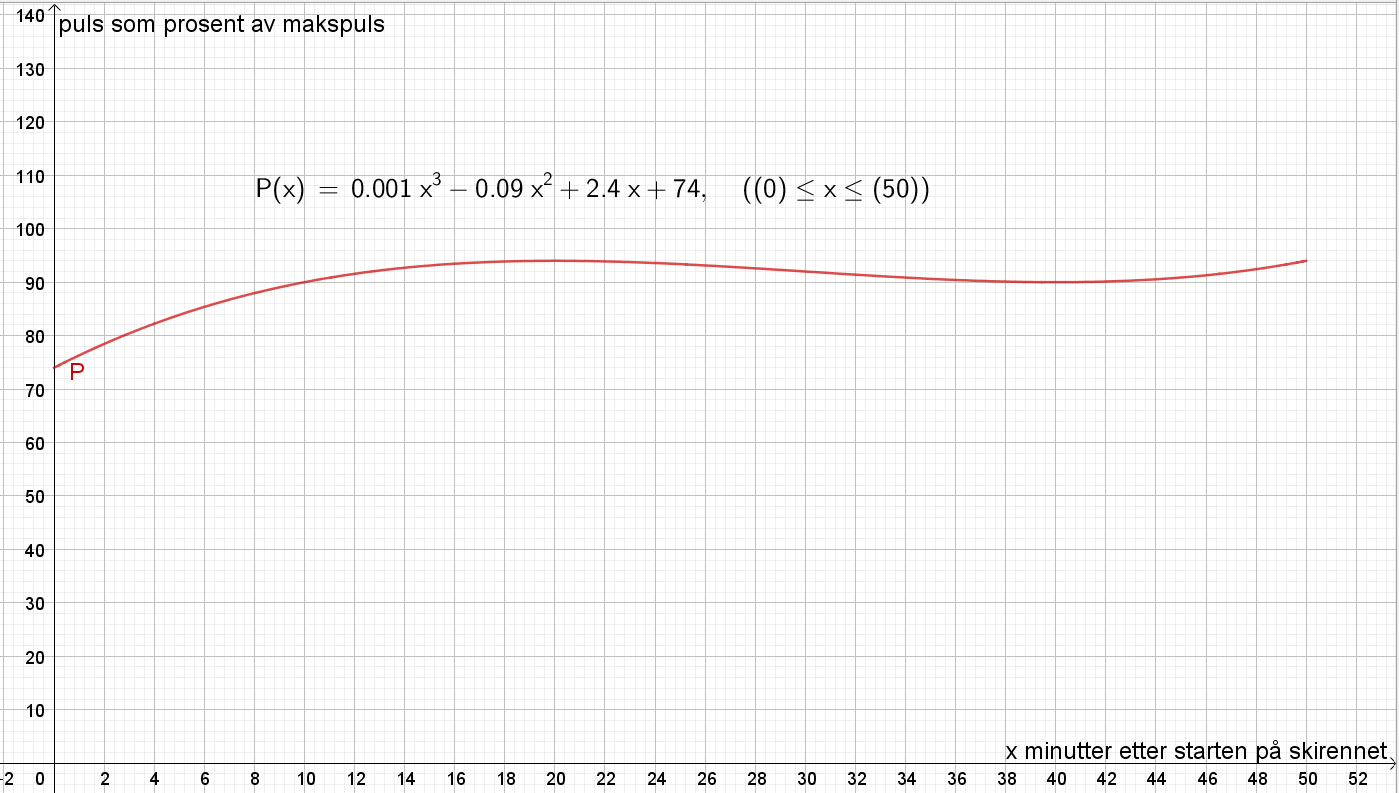
Bruker Geogebra til å tegne grafen til P.

b)

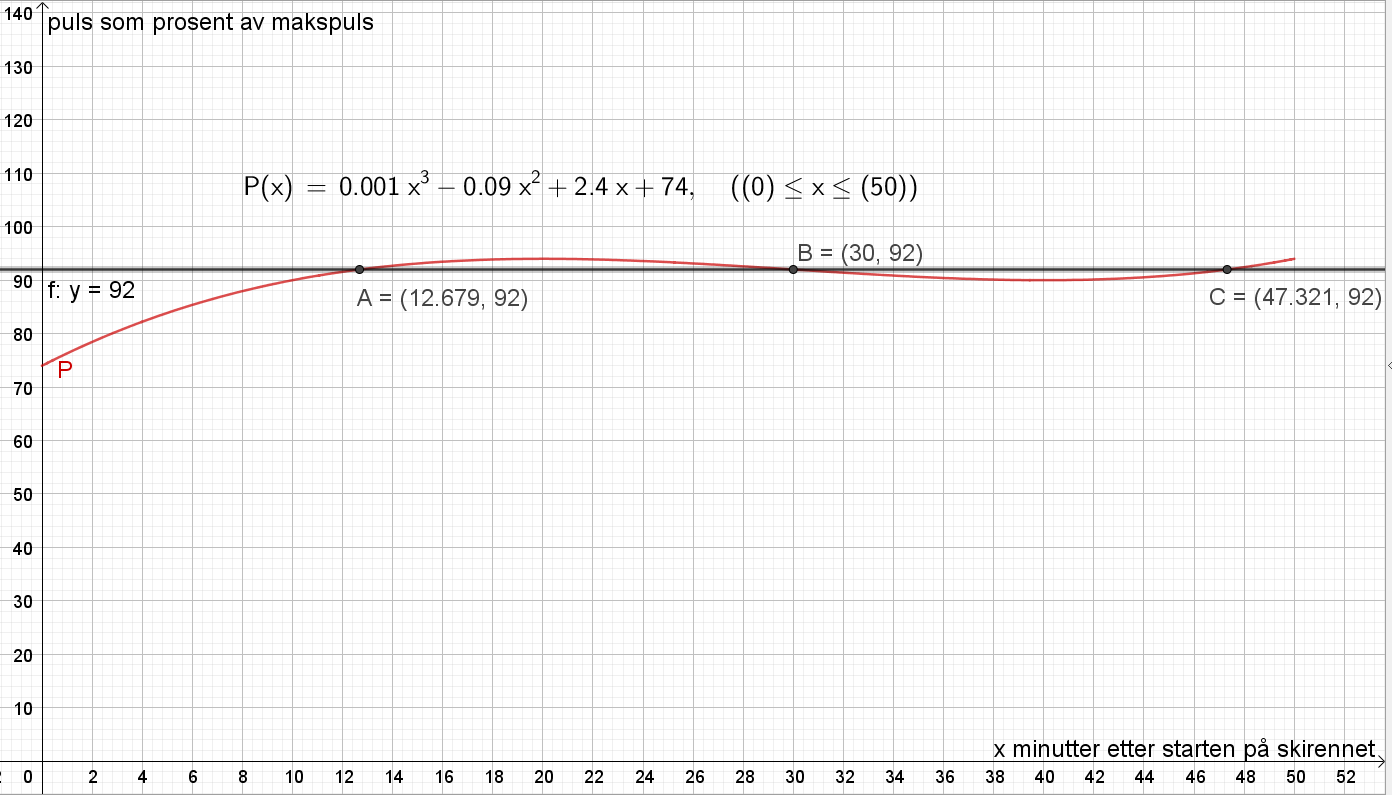
Legger inn linja y = 92, og bruker "Skjæring mellom to objekt" for å finne skæringspunktene mellom denne linjen og grafen til $P$. Leser av x-verdien til skjæringspunktene A, B og C, og beregner antall minutter hvor Ole hadde høyere enn 92% av makspuls:

$(30-12.7)+(50-47.3) = 20$

Pulsen til Ole høyere enn 92 % av makspuls i 20 minutter.

c)

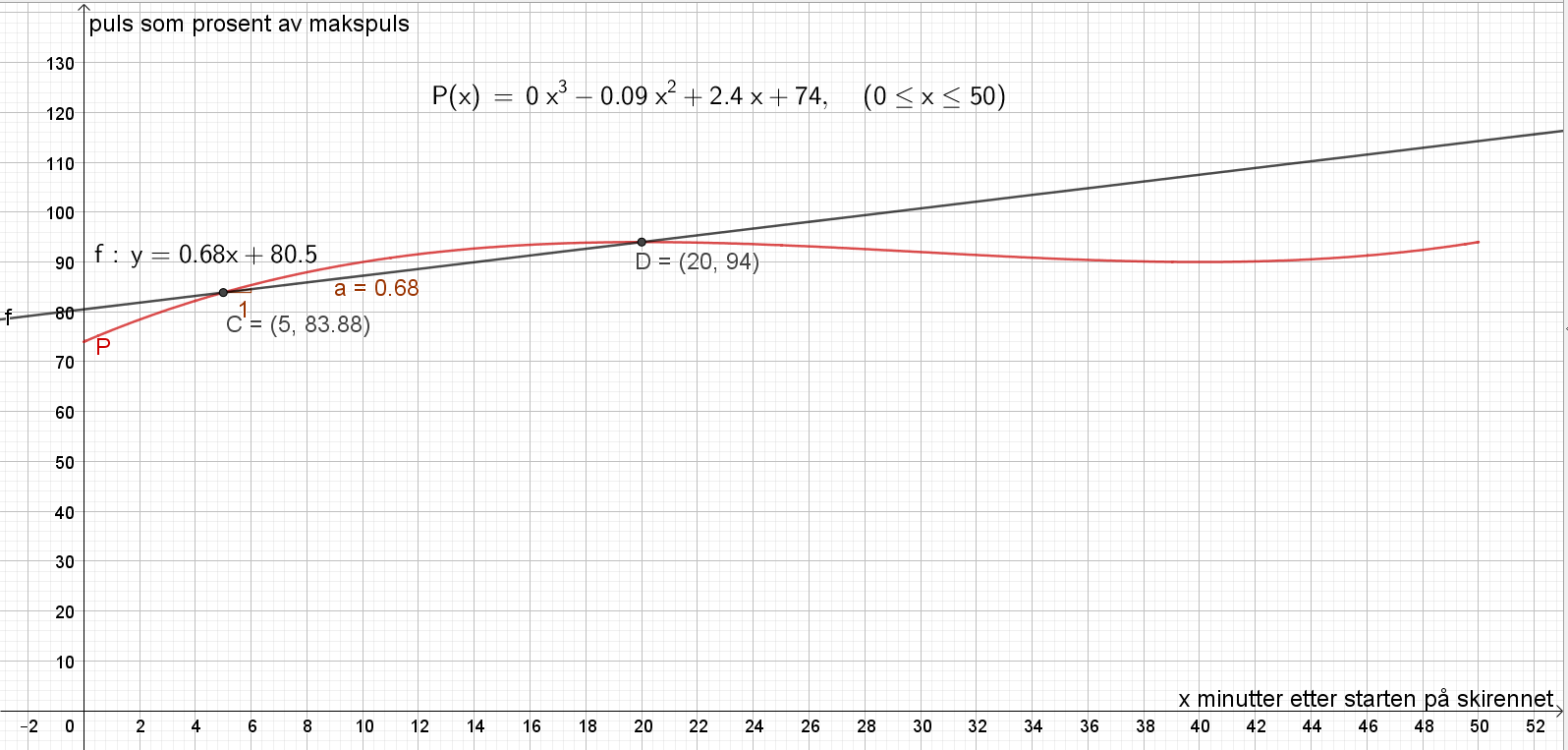
Bruker Geogebra. Lager punktene (5,P(5)) og (20,P(20)). Lager en linje mellom de to punktene. Bruker knappen "stigning" og finner at stigningstallet til den rette linjen er 0,68. Det betyr at mellom 5 minutter og 20 minutter etter starten på skirennet, øker pulsen til Ole med gjennomsnittlig 0,68 % av makspuls per minutt.

Oppgave 2

a)

$H=\frac{d\cdot v}{60\cdot t}=\frac{20\cdot 240}{60\cdot 2}=40$

Drypphastigheten er 40 dråper per minutt.

b)

Dersom t dobles og d og v ikke endres, vil H halveres. Dette fordi å doble en nevner vil si at H halveres.

c)

Bruker CAS i Geogebra.

Denne pasienten skal ha 360 mL av den intravenøse væsken.

Oppgave 3

a)

Provisjon: $\frac{0,5}{100}\cdot 5300000 \, kr =26500\, kr$

Total lønn i september: $12000\,kr+26500\,kr=38500\,kr$

Timelønn i september: $\frac{38500\,kr}{186\,t} \approx 207 kr/t$

Saras brutto timelønn i september ble 207 kroner per time.

b)

Trekkgrunnlag i september: $0,98\cdot 38500\, kr = 37730\,kr$

Nettolønn i september: $0,64\cdot 37730\,kr = 24147,2\,kr$

c)

Bruttolønn i oktober: $180\,t \cdot 282\,kr/t = 50760\,kr$

Provisjon: $50760\,kr-12000\,kr = 38760\,kr$

Salgssum for eiendommene Sara solgte i oktober: $\frac{38760\,kr}{0,005}=7752000\,kr$