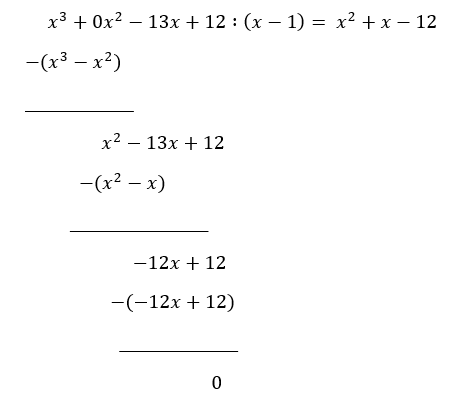R1 2018 vår LØSNING

Oppgaven som pdf (scannet)

Diskusjon av denne oppgaven på matteprat

Løsningsforslag (pdf) (open source, meld fra om forbedringer eller feil her)

Løsningsforslag av LektorNilsen (pdf)

Løsning som video av Lektor Håkon Raustøl

DEL 1

Oppgave 1

a)

$f(x)=x^4-x+2$

$f'(x)=4x^3-1$

b)

$g(x)=x^3\cdot ln(x)$

$g'(x)=3x^2\cdot ln(x) + x^3 \cdot \frac{1}{x} = 3x^2ln(x)+x^2$

c)

$h(x)=e^{2x^2+x}$

$h'(x)=(4x+1)e^{2x^2+x}$

Oppgave 2

a)

$\frac{1}{2x-2}+\frac{2}{x-3}-\frac{x-2}{x^2-4x+3} \\ = \frac{1\cdot \color{blue}{(x-3)}}{2(x-1)\color{blue}{(x-3)}}+\frac{2\cdot \color{red}{2(x-1)}}{\color{red}{2(x-1)}(x-3)}-\frac{\color{orange}{2}(x-2)}{\color{orange}{2}(x-1)(x-3)} \\ =\frac{ (x-3) + (4x-4) - (2x-4)}{2(x-1)(x-3)} \\ = \frac{x+4x-2x -3-4+4}{2(x-1)(x-3)} \\ = \frac{3x-3}{2(x-1)(x-3)} \\ = \frac{3(x-1)}{2(x-1)(x-3)} \\ = \frac{3}{2(x-3)} \\ = \frac{3}{2x-6}$

b)

$2ln(x\cdot y^3)-\frac{1}{2}ln(\frac{x^4}{y^2}) \\ = 2(ln(x)+ln(y^3))-\frac{1}{2}(ln(x^4)-ln(y^2)) \\= 2(ln(x)+3ln(y))-\frac{1}{2}(4ln(x)-2ln(y)) \\= 2ln(x)+6ln(y)-2ln(x)+ln(y) \\= 7ln(y)$

Oppgave 3

Vi har punktene A(-2,-1), B(-1, -3), C(3, -1) og D(t,t^2+2) der $t\in R$.

a)

$\vec{AB} = [-1-(-2), -3-(-1)] = [1, -2]$

$\vec{BC} = [3-(-1), -1-(-3)] = [4, 2]$

b)

$[1,-2]\cdot[4,2] = 1\cdot 4 + (-2)\cdot 2 = 4-4 = 0$

Skalarproduktet av $\vec{AB}$ og $\vec{BC}$ er 0, og vi har derfor $\vec{AB}\perp\vec{BC}$

c)

$\vec{CD}=[t-3, t^2+2-(-1)] = [t-3, t^2+3]$

Dersom $\vec{CD}\| \vec{AB}$, så er $\vec{CD} = k\cdot\vec{AB}$

$[t-3,t^2+3]=k\cdot[1,-2]$

Vi får likningssettet:

$I \quad t-3 = k$

$II \quad t^2+3=-2k$

$II \quad t^2+3 = -2 (t-3) \\ \quad t^2 + 3 = -2t+6 \\ \quad t^2 + 2t -3 = 0 \\ \quad (t+3)(t-1) = 0 \\ \quad t = -3 \vee t = 1$

$\vec{CD}\| \vec{AB}$ når $ t = -3 \vee t = 1$.

Oppgave 4

Vi har $f(x)=x^3+k\cdot x + 12$

a)

Dersom $f(x):(x-1)$ skal gå opp, er x=1 et nullpunkt.

$f(1)=0 \\ 1^3+k\cdot 1 + 12 = 0 \\ k+13 = 0 \\ k=-13$

b)

Vi har nå $f(x)=x^3-13x+12$

Utfører polynomdivisjonen:

$f(x)=(x^2+x-12)(x-1) = (x-3)(x-1)(x+4)$

c)

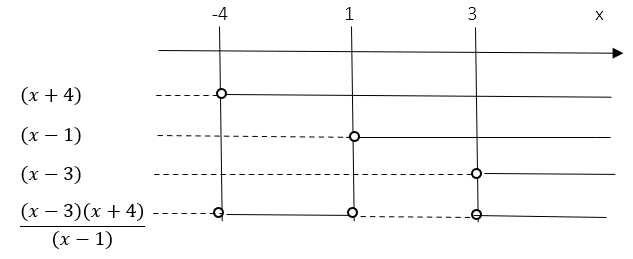
$\frac{x^2+x-12}{x-1} \geq 0 \\ \frac{(x-3)(x+4)}{x-1} \geq 0$

$\frac{x^2+x-12}{x-1} \geq 0$ nå $x\in [-4,1]\cup [3,\rightarrow \rangle$

Oppgave 5

D = defekt

a)

$P(A \cap D) = 0,40 \cdot 0,03 = 0,012 = 1,2 \%$

Sannsynligheten for at laderen kommer fra leverandør A og er defekt, er 1,2%.

b)

$P(D)=P(D|A)\cdot P(A) + P(D|B)\cdot P(B) \\= 0,03\cdot 0,40 + 0,02 \cdot 0,60 = 0,012 + 0,012 = 0,024$

$P(A | D) = \frac{P(A) \cdot P(D|A)}{P(D)} = \frac{0,40 \cdot 0,03}{0,024} = \frac{0,012}{0,024} = 0,5 = 50\%$

Sannsynligheten for at en lader som er defekt, kommer fra leverandør A, er 50%.

Oppgave 6

Vi har $f(x)=e^{2x}-4e^x+3$

a)

$f(x)=0 \\ e^{2x}-4e^x+3 = 0 \\ \text{Setter} \,u = e^x \\ u^2 - 4u + 3 = 0 \\ (u-1)(u-3)=0 \\ u= 1 \vee u = 3 \\ e^x = 1 \vee e^x = 3 \\ x = ln 1 \vee x = ln 3 \\ x = 0 \vee x \approx 1,10 $

Nullpunktene til f er (0,0) og (1.10, 0).

b)

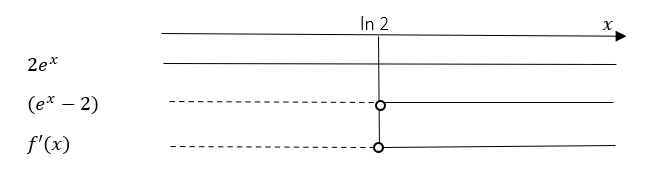
$f'(x)= 2e^{2x}-4e^x$

$f'(x)=0 \\ 2e^{2x}-4e^x = 0 \\ 2e^x(e^x-2)\\ \text{Setter} \,u = e^x \\ 2u(u-2)= 0 \\ u = 0 \vee u = 2 \\ e^x = 0 \vee e^x = 2 \\ \xcancel{x = ln 0} \vee x = ln 2 \\ x = ln 2 \approx 0,69$

Forkaster $x = ln 0$ da $ln 0 $ ikke er definert.

Finner funksjonsverdien i x = ln 2.

$f(ln 2) = e^{2(ln2)}-4e^{ln2} + 3 = e^{ln2^2}-4\cdot 2 + 3 = 4-8+3 = -1$

Grafen til f har et bunnpunkt i (0.69, -1).

c)

$f' '(x)=4e^{2x}-4e^x = 4e^x(e^x-1)$

$f' '(x)=0 \\ 4e^x(e^x-1) = 0 \\ 4e^x = 0 \vee e^x = 1 \\ \xcancel{x = ln0} \vee x=ln1 \\ x=0$

Finner funksjonsverdien i x = 0.

$f(0)=e^{2\cdot 0}-4e^0+3 = 1-4+3 = 0$

Grafen til f har et vendepunkt i (0,0).