Statistikk I: Forskjell mellom sideversjoner
| Linje 13: | Linje 13: | ||
178, 142, 156, 162, 154 , 156, 163, 169, 172, 142, 156, 172, 173, 161, 169 | 178, 142, 156, 162, 154 , 156, 163, 169, 172, 142, 156, 172, 173, 161, 169 | ||
<p></p> | <p></p> | ||
Vi kan sette resultatet opp i en tabell: | Vi kan sette resultatet opp i en tabell | ||
: | |||
<table border="1" cellpadding="5"> | |||
<table border="1" cellpadding=" | |||
<tr> | <tr> | ||
<td>'''Høyde ''x'' '''</td> | <td>'''Høyde ''x'' '''</td> | ||
Sideversjonen fra 18. aug. 2010 kl. 20:56
Innledning
Statistikk er å bearbeide tallmaterialet / data slik at man forhåpentligvis kan observere en trend eller tendens. I beste fall kan man trekke en konklusjon. Tallmaterialet skaffes ofte ved hjelp av spørreundersøkelser, målinger eller observasjoner. Statistikk kan presenteres i forskjellige former og det kan være en god måte å speile virkeligheten på. Statistikk kan også, uten å være direkte feil, presenteres på en måte som tåkelegger virkeligheten. I slike tilfeller er det ofte interessegrupper som presenterer et tallmaterialet med det formål å fremme sin sak. VÆR PÅ VAKT, i slike tilfeller er statistikk mer forvirrende en forklarende.
Frekvenstabell
Eksempel
En liten skoleklasse har femten elever. Høyden på elevene målt i cm. er slik:
178, 142, 156, 162, 154 , 156, 163, 169, 172, 142, 156, 172, 173, 161, 169
Vi kan sette resultatet opp i en tabell
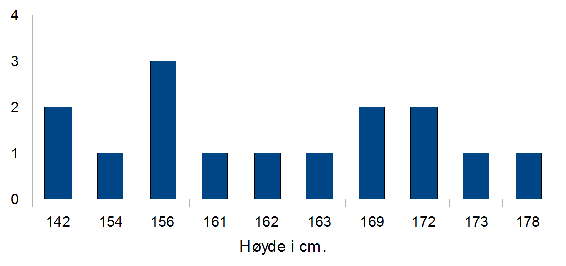
Høyde x Frekvens f 142 2 154 1 156 3 161 1 163 1 169 2 172 2 173 1 178 1 N = 15 N er antall målinger, i dette tilfellet antall elever. Man ser at frekvensen er 3 for høyden 156 cm.
Søylediagram
Med frekvens mener vi hvor mange ganger en verdi forekommer. Tabellen kan presenteres som den er, eller vi kan presentere den som et diagram. Et eksempel kan være et søylediagram. På y aksen har vi antall observasjoner og på x aksen har vi de forskjellige type observasjoner.
På y aksen har man antall eller frekvens, og på x aksen høyden
Gjennomsnitt
Gjennomsnitt er summen av alle verdier delt på antall verdier.
| Høyde x | Frekvens f | Sum høyde f <tex> \cdot </tex> x |
| 142 | 2 | 2 <tex> \cdot </tex> 142 |
| 154 | 1 | 154 |
| 156 | 3 | 3 <tex>\cdot </tex> 156 |
| 161 | 1 | 161 |
| 163 | 1 | 163 |
| 169 | 2 | 2<tex>\cdot </tex> 169 |
| 172 | 2 | 2<tex>\cdot </tex> 172 |
| 173 | 1 | 173 |
| 178 | 1 | 178 |
| N = 15 | S = |
Median
Median er den midterste verdien etter alle verdien er blitt sortert i stigende rekkefølge. Dersom antall verdier er parttall (2,4,6.....) er median gjennomsnittet av de to midterste verdiene.
Eksempel 3:
Datamengden er 10, et parttall. Median blir gjennomsnittet av 3 og 3 som er (3+3)/2=3
Typetall
Typetallet er den verdi som det er flest forekomster av i datamengden. I vårt eksempel er typetallet 3, fordi det forekommer flest (4) ganger.
histogram
Histogrammet på statistikksiden vår (se link i venstremarg) har klasser som alle har lik klassebredde. Slik trenger det ikke å være.
Eksempel: Eva lurer på hvor mange telefoner hun får inn på kontoret en dag og bestemmer seg for å telle. Resultatet setter hun opp i en frekvenstabell:
Her ser man at tidsintervallene, altså klassebredden, varierer fra en time til tre timer.
Her må man behandle hver klasse for seg. Høyden på klassen eller diagramhøyden / histogramhøyden finnes ut fra formelen:
Om man tenker på frekvensen som et areal ser man lett at formelen over må være riktig.
Ved å bruke formelen over og informasjonen i frekvensdiagrammet kan vi tegne histogrammet:
Fra histogrammet ser vi at det kommer inn flest telefoner per time i perioden tolv til to.