Trapes: Forskjell mellom sideversjoner
Fra Matematikk.net
m Teksterstatting – «</tex>» til «</math>» |
Hele setninger. Lenke til relaterte figurer. |
||
| Linje 1: | Linje 1: | ||
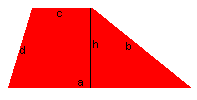
Et '''trapes''' er en firkant der to sider er parallelle. | |||
Arealet av trapesen er | |||
:<math> | |||
\displaystyle | |||
A = \frac {h(a + c)}{2} | |||
</math> | |||
når $h$ er høyden mellom de parallelle sidene og $a$ og $b$ er lengdene av de to parallelle sidene. | |||
[[Bilde:Trapes.gif]] | [[Bilde:Trapes.gif]] | ||
De følgende figurene er spesialtilfeller av trapes: | |||
* [[Parallellogram]]: En firkant der to og to sider er parallelle. | |||
* [[Rombe]]: En parallellogram der alle sidene er like lange. | |||
* [[Rektangel]]: En firkant der to og to sider er parallelle og alle vinklene er rette. | |||
* [[Kvadrat]]: En rektangel der alle sidene er like lange. | |||
---- | ---- | ||
[[kategori:lex]] | [[kategori:lex]] | ||
Sideversjonen fra 27. okt. 2019 kl. 20:49
Et trapes er en firkant der to sider er parallelle.
Arealet av trapesen er
- <math>
\displaystyle A = \frac {h(a + c)}{2}
</math>
når $h$ er høyden mellom de parallelle sidene og $a$ og $b$ er lengdene av de to parallelle sidene.
De følgende figurene er spesialtilfeller av trapes:
- Parallellogram: En firkant der to og to sider er parallelle.
- Rombe: En parallellogram der alle sidene er like lange.
- Rektangel: En firkant der to og to sider er parallelle og alle vinklene er rette.
- Kvadrat: En rektangel der alle sidene er like lange.