Løsning del 2 utrinn Vår 19: Forskjell mellom sideversjoner
| Linje 128: | Linje 128: | ||
$hs = \sqrt{(21,65m)^2 + (17,5m)^2} = 27,84$ | $hs = \sqrt{(21,65m)^2 + (17,5m)^2} = 27,84$ | ||
Arealet av en sideflate blir da | |||
1948, | $ \frac{35m \cdot 27,84m}{2} = 487,17 m^2$ | ||
Og arealet av hele overflaten blir | |||
$ 4 \cdot 487,17 m^2 = 1948,68m^2 \approx 1950 m^2$ | |||
===c)=== | ===c)=== | ||
Sideversjonen fra 5. jun. 2019 kl. 03:12
Løsningsforslag lagt ut på Facebookgruppen Matematikkdidaktikk
Oppgave 1
a)
b)
Variasjonsbredden er største minus minste verdi:
17 098 240 $km^2$ - 8 515 770 $km^2$ = 8 582 470 $km^2$
c)
".... enn arealet av Brasil." Betyr at det er arealet av Brasil man skal sammenligne med:
$\frac{17098240}{8515770} \cdot 100$ % = 200,78%, altså er Russland over dobbelt så stort som Brasil i areal.
Oppgave 2
a)
Vi avleser y aksen og ser at grafen slutter på ca. 6200 km.
b)
På x aksen ser vi at mellom 1 og 6 timer er grafen parallell med x aksen, hvilket betyr at avstanden fra Oslo ikke endrer seg, dvs. hun har en pause på fem timer.
c)
Vi ser fra kartet at New York ligger seks timer etter Oslo. I Oslo er klokka 18:55 når hun lander, det betyr at klokka i New York er 12:55.
Oppgave 3
a)
$2 \cdot 27 + 22 = 76$ GBP
Multiplisert med 11 blir det ca. 836 NOK.
b)
377m = 0,377 km
30 min = 0,5 h
$0,377 : 0,5 = 0,754 $km/h
c)
Forholdet mellom lengde og høyde er 5:3. Dersom lengden til et flagg er 7,5 m er høyden $ \frac{7,5m}{5} \cdot 3 = 4,5 m$
Bredden på stripen er $\frac 15$ av dette, altså $\frac{4,5}{5} = 0,9 m.$
Oppgave 4
Oppgave 5
a)
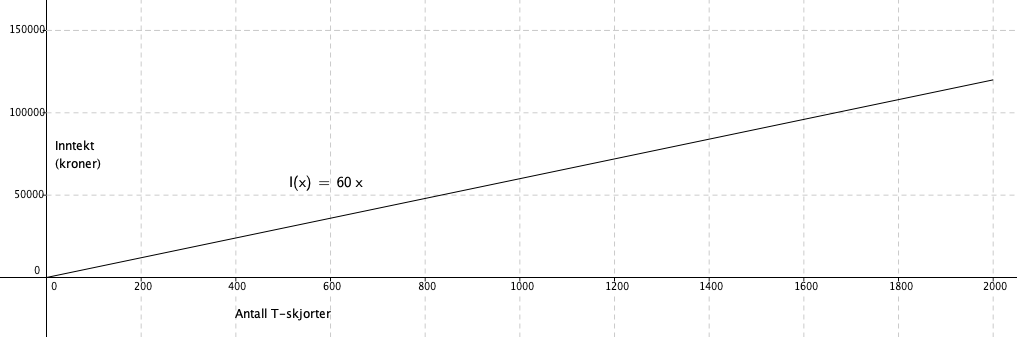
Prisen for en T - skjorte er 60 kroner.
b)
c)
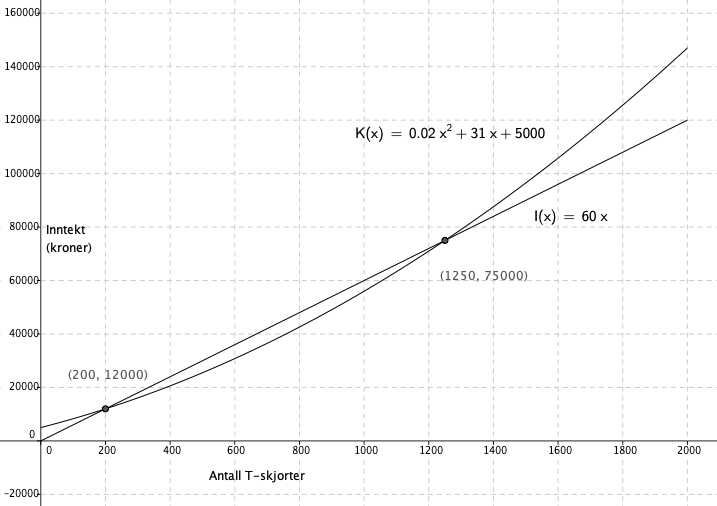
d)
For at inntektene skal være større enn kostnadene må salget være mer enn 200 og mindre enn1250 T - skjorter. Se figur i c.
Oppgave 6
a)
$365:29,5= 12$
Månen går 12 hele runder rundt jorda i løpet av et år.
b)
$O = 2 \pi \cdot \sqrt{0,5\cdot (a^2 + b^2)} = \\ 2 \pi \cdot \sqrt{0,5\cdot (405000^2 + 363000^2)} = \\ 24.166.348 km$
Omkretsen er ca. 24,2 millioner kilometer.
Oppgave 7
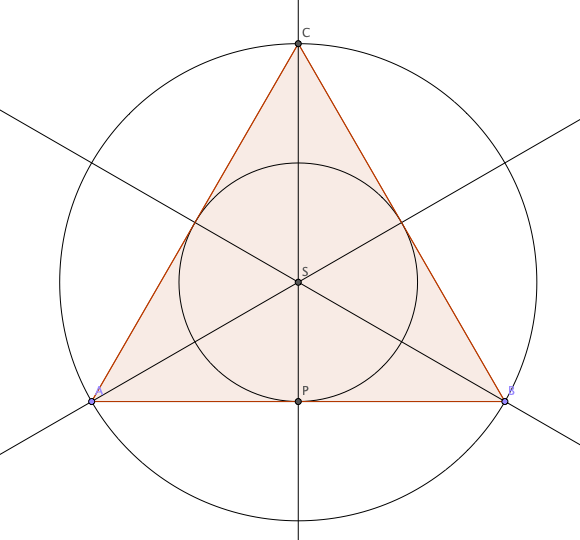
Her er et forslag av mange mulige løsninger.
Avsatte AB 10 cm. Laget regulær trekant. Halverte vinklene for å finn S. Slo den omskrevne sirkelen. Fant P og slo den innskrevne sirkelen.
Oppgave 8
a)
b)
c)
Oppgave 9
a)
I en kvadratisk grunnflate er alle sidene like lange.
$ \sqrt{1225 m^2} = 35m$
b)
Finner først avstanden fra toppen av pyramiden, til midt nede på sidekanten (hs). Finner så arealet av en side, og multipliserer med fire.
$hs = \sqrt{(21,65m)^2 + (17,5m)^2} = 27,84$
Arealet av en sideflate blir da
$ \frac{35m \cdot 27,84m}{2} = 487,17 m^2$
Og arealet av hele overflaten blir
$ 4 \cdot 487,17 m^2 = 1948,68m^2 \approx 1950 m^2$