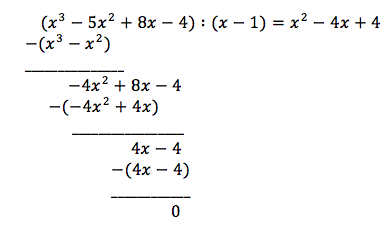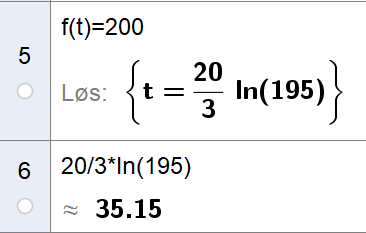S2 2018 høst LØSNING

Diskusjon av oppgaven på matteprat

DEL 1

Oppgave 1

a)

$f(x)=e^{2x} \\ f'(x)=2e^{2x}$

b)

$g(x)=\frac{x^4-1}{x^2} \\ g'(x)=\frac{4x^3 \cdot x^2 - (x^4-1) \cdot 2x }{(x^2)^2} \\ =\frac{4x^5-2x^5+2x}{x^4} \\ =\frac{2x^5+2x}{x^4} \\ = \frac{2x^4+2}{x^3}$

c)

$h(x)=x^3 \cdot ln\, x \\ h'(x)=3x^2 \cdot ln \, x + x^3 \cdot \frac{1}{x} \\ = 3x^2 \cdot ln \, x + x^2$

Oppgave 2

Dersom $-1<k<1$ i en geometrisk tallfølge $a_n=a_1k^{n-1}$ sier vi at den konvergerer.

I slike tilfeller er $\lim_{n\to\infty}S_n=\lim_{n\to\infty}\sum_{i=1}^n a_i=\frac{a_1}{1-k}$

a)

Vi har rekken $a_n=54 \cdot \frac{1}{3}^{n-1}$. I denne rekka er $k= \frac{1}{3}$. Det vil si at rekken konvergerer. Summen er gitt ved:

$\lim_{n\to\infty}S_n=\frac{54}{1-\frac{1}{3}} = \frac{54}{\frac{2}{3}} = \frac{54 \cdot 3}{2} = 81$

b)

Vi har rekken $a_n=4 \cdot (-2)^{n-1}$. I denne rekka er $k= -2$. Det vil si at rekken ikke konvergerer.

Oppgave 3

a)

x runder løpt	1	2	3	4	$n$
f(x) kroner tjent per runde	10	15	20	25	$F_n$
utregning for å finne formel	$5\cdot 2$	$5\cdot 3$	$5\cdot 4$	$5\cdot 5$	$5\cdot(n+1) = 5n+5$

Inntekten per runde $F_n$ er gitt ved $F_n=5n+5$, der x er antall runder løpt og $n>0$. Setter $F_n=100$

$5n+5=100 \\ n+1 = 20 \\ n=19$

Lise må løpe 19 runder for å tjene 100 kroner på den siste runden.

b)

$ S=\sum_{n=1}^{25} 5n+5 \\ = \frac{(5\cdot 1 + 5)+(5\cdot 25 + 5)}{2} \cdot 25 \\ = \frac{10+130}{2} \cdot 25 \\ = 70 \cdot 25 = 1750 $

Bedriften må gi totalt 1750 kroner dersom Lise løper 25 runder.

Oppgave 4

a)

Funksjonen f er delelig på (x-1), derfor er (x-1) en faktor i f(x).

b)

Vi har allerede funnet en faktor, nemlig (x-1).

Faktoriserer nå resten ved å kjenne igjen andre kvadratsetning:

$x^2-4x+4=x^2-2\cdot 2 + 2^2=(x-2)(x-2)$

Vi har da:

$f(x)=x^3-5x^2+8x-4=(x-1)(x-2)(x-2)$

c)

Kjenner igjen konjugatetningen i nevneren.

$\frac{x^3-5x^2+8x-d}{x^2-4}=\frac{x^3-5x^2+8x-d}{(x+2)(x-2)}$

Brøken kan forkortes for d=4, slik vi hadde for f(x), hvor (x-2) var en faktor.

Oppgave 5

a)

$I(p)=p\cdot q(p)=p\cdot 500\cdot e^{-0,04p}$

Finner størst inntekt ved derivasjon:

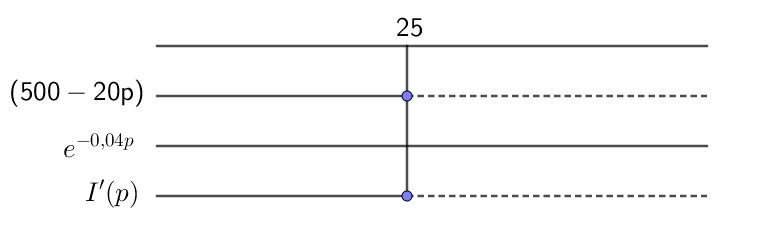
$I'(p)=500 \cdot e^{-0,04p} + 500p \cdot (-0,04) \cdot e^{-0,04p} \\ = 500 \cdot e^{-0,04p} -20p \cdot e^{-0,04p} \\ =(500-20p)\cdot e^{-0,04p}$

$I'(p)=0 \\ (500-20p)\cdot e^{-0,04p}=0 \quad \Rightarrow \quad (500-20p)=0 \\ p=\frac{500}{20}=25 $

Vi har et toppunkt i p=25. Det vil si at en pris på 25 kr gir maksimal inntekt.

b)

$q=500\cdot e^{-0,04p} \\ \frac{q}{500}=e^{-\frac{1}{25} p} \\ ln \lgroup \frac{q}{500} \rgroup=-\frac{1}{25} p \\ -25\, ln \lgroup \frac{q}{500}\rgroup=p \\ p(q)=-25\, ln \lgroup \frac{q}{500}\rgroup$

c)

$p(q)=-25\, ln \lgroup \frac{q}{500}\rgroup$

$p'(q)=p'(u)\cdot u' \quad ,u=\frac{q}{500}$

$p'(q)=-25 \cdot \frac{1}{u} \cdot u'$

$p'(q)=-25 \cdot \frac{1}{\frac{q}{500}} \cdot \frac{1}{500} =-\frac{25}{q} \\ p'(25)=-\frac{25}{25}=-1$

Svaret forteller oss at ved en etterspørsel på 25 enheter, vil prisen synke med 1 krone per enhet, dersom etterspørselen blir 26 enheter.

Oppgave 6

a)

Vi har $f(x)=ax^3+bx^2+cx+d$, der a,b,c og d er konstanter.

• x=1 er et nullpunkt, det vil si at $f(1)=0$ .

$\quad f(1)=a\cdot 1^3 + b \cdot 1^2 + c\cdot 1 + d = a+b+c+d=0$

• x=-2 er et nullpunkt, det vil si at $f(-2)=0$.

$\quad f(-2)=a\cdot(-2)^3+b\cdot(-2)^2+c\cdot(-2)+d=-8a+4b-2c+d=0$

• x=1 er ekstremalpunktet, det vil si at $f'(1)=0$.

$\quad f'(x)=3ax^2+2bx+c\\ \quad f'(1)=3a\cdot 1^2 + 2b\cdot 1+c=3a^2+2b+c=0$

• At grafen til f skjærer y-aksen i y=2 forteller oss at konstantleddet d=2.

b)

Bruker at d=2. Bruker likning 1 til å finne et uttrykk for c:

$a+b+c+d=0 \quad \Rightarrow \quad c=-a-b-2$

Setter inn uttrykket for c i likning 2:

$-8a+4b-2c+2=0 \\ -8a+4b-2(-a-b-2)+2=0 \\ -8a+4b+2a+2b+4+2=0 \\ -6a+6b+6=0 \quad |:6 \\-a+b+1=0$

Setter inn uttrykket for c i likning 3:

$3a+2b+c=0 \\ 3a+2b+(-a-b-2)=0 \\ 3a+2b-a-b-2=0 \\ 2a+b-2=0$

Har nå to likninger med to ukjente:

$-a+b+1=0 \\ 2a+b-2=0$

Finner et uttrykk for b:

$-a+b+1=0 \quad \Rightarrow \quad b=a-1$

Finner a:

$2a+b-2=0 \\ 2a+(a-1)-2=0 \\ 3a-3=0 \\ a=1$

Finner b:

$b=a-1=1-1=0$

Finner c ved hjelp av mitt tidligere uttrykk for c:

$c=-a-b-2=-1-0-2=-3$

Bestemmer et uttrykk for f(x):

$f(x)=1x^3+0x^2-3x+2 = x^3-3x+2$

Oppgave 7

a)

La X være gevinsten spilleren får når terningen kastes én gang.

x	0	20	60	200
$P(X=x)$	$\frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{6}$	$\frac{1}{6}$

b)

Finner forventningsverdien $E(x)=\mu$

$\mu=0\cdot P(X=0) + 20\cdot P(X=20) + 60\cdot P(X=60)+ 200\cdot P(X=200) \\ = 0 + 20\cdot \frac{1}{3} + 60\cdot \frac{1}{6} + 200\cdot \frac{1}{6} \\ = \frac{20}{3}+\frac{30}{3} +\frac{100}{3} = \frac{150}{3} = 50 $

Forventningsverdien er 50 kroner.

Finner variansen $Var(X)$

$Var(X)=(0-\mu)^2\cdot P(X=0) + (20-\mu)^2\cdot P(X=20) + (60-\mu)^2\cdot P(X=60)+ (200-\mu)^2\cdot P(X=200) \\ = (0-50)^2 \cdot \frac{1}{3} + (20-50)^2 \cdot \frac{1}{3} +(60-50)^2 \cdot \frac{1}{6} + (200-50)^2 \cdot \frac{1}{6} \\ = \frac{2500}{3}+\frac{900}{3} +\frac{100}{6} + \frac{22500}{6}\\ = \frac{2500}{3}+\frac{900}{3} +\frac{50}{3} + \frac{11250}{3}\\ =\frac{14700}{3}=4900$

Finner $SD(X)=\sqrt{Var(X)}$

$SD(X)=\sqrt{4900} = 70$

c)

Prisen per spill må være 60 kroner dersom jeg som arrangør i det lange løp skal få et overskudd på 10 kroner per spill.

d)

S er ifølge sentralgrensesetningen tilnærmet normalfordelt, fordi vi gjentar spillet 100 ganger. Sentralgrensesetningen sier følgende:

La X være en stokastisk variabel med forventningsverdi $\mu$ og standardavvik $\sigma$.

La $\Sigma_n X$ være summen av n uavhengige forsøk med X.

For store verdier av n er $\Sigma_n X$ tilnærmet normalfordelt.

e)

$E(X)=-10$ fordi forventningsverdien for spilleren er -10 kroner per spill.

$E(S)=\mu=n\cdot \mu = 100\cdot (-10) = -1000$

Det betyr at forventningsverdien for 100 spill er -1000 kroner.

Standardavviket for gevinst er det samme som før, SD(X)=70.

$SD(S)=\sigma =\sqrt{n} \cdot \sigma = \sqrt{100} \cdot 70 = 10 \cdot 70 = 700$

Det betyr at standardavviket for 100 spill er 700 kroner.

f)

$P(S>0)=1-P(S<0)\\=1-\Phi \lgroup \frac{0-\mu}{\sigma} \rgroup \\= 1- \Phi \lgroup \frac{0-(-1000)}{700} \rgroup \\= 1-\Phi \lgroup \frac{10}{7} \rgroup \\= 1-\Phi(1,43) \\=1-0,9236=0,0764$

Sannsynligheten for at spilleren går i overskudd med de 100 spillene er 0,0764 = 7,64%.

DEL 2

Oppgave 1

a)

Bruker CAS i Geogebra til å finne et uttrykk for overskuddet, O(x)

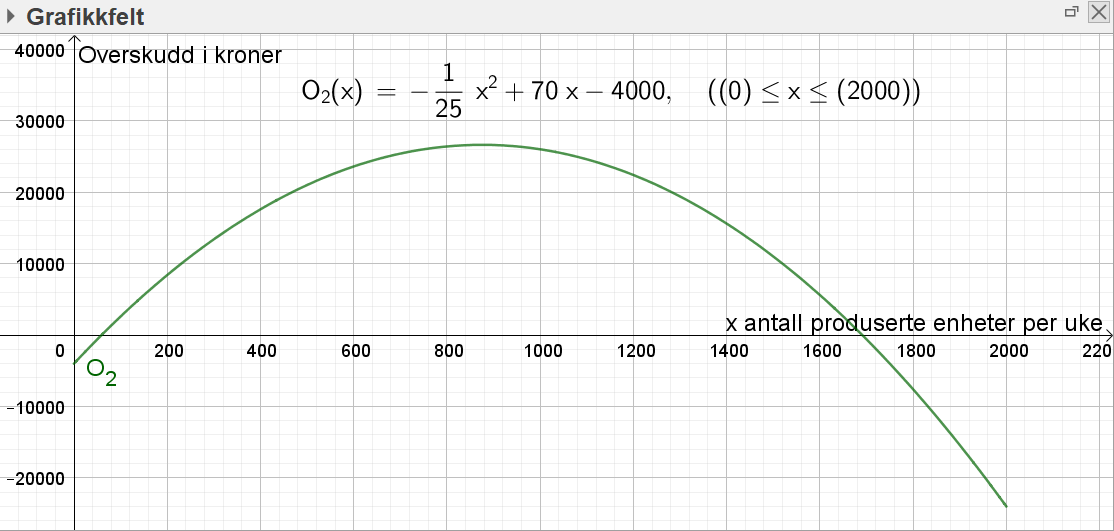
Bruker Geogebra til å tegne grafen til $O_2(x)$.

b)

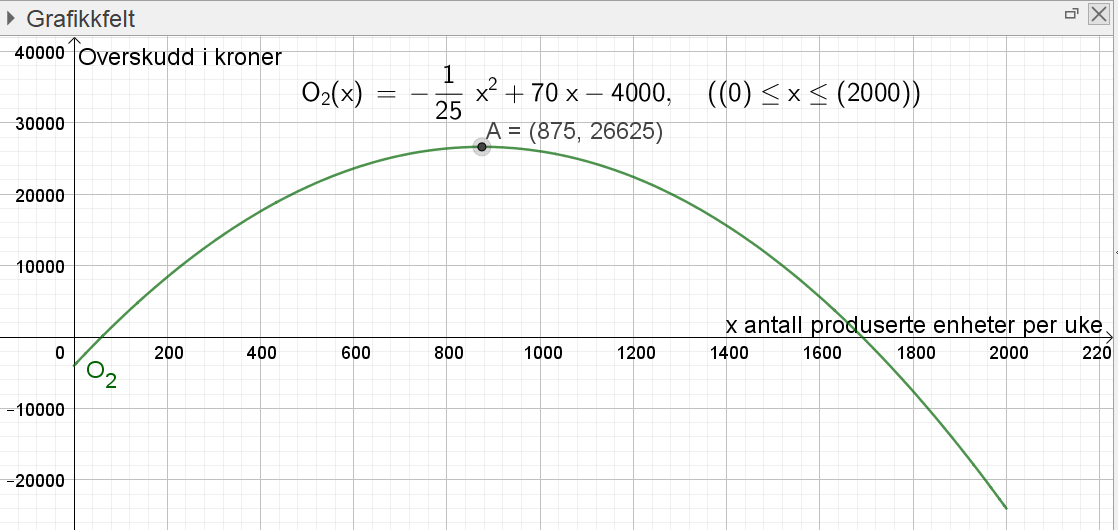
Bruker kommandoen $Ekstremalpunkt[O_2]$ til å bestemme den produksjonsmengden som gir størst overskudd.

Den produksjonsmengden som gir størst overskudd er 875 enheter i uka, se punkt A.

c)

Jeg finner ekstremalpunkt for a(x), kostnad per enhet, i x=400 og x=-400. Forkaster x=-400, siden vi bare ser på $x\in \langle 0 , 2000 \rangle$. Sjekker at det er et bunnpunkt (og ikke et toppunkt) i x=400 ved å se at funksjonen synker i x=350 og øker i x=450.

Den produksjonsmengden som gir lavest kostnad per enhet, er 400 enheter i uka.

Oppgave 2

a)

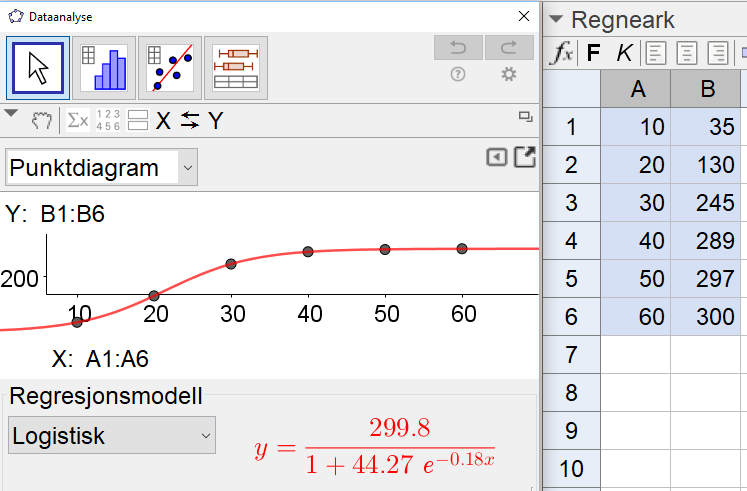
Bruker Geogebra til å utføre en regresjonsanalyse. Velger logistisk regresjonsmodell.

En funksjon som beskriver sammenhengen mellom tiden t og antall skadedyr i dette huset, er

$g(t)=\frac{299,8}{1+44,27e^{-0,18t}}$

b)

Bruker CAS i Geogebra til å løse oppgaven.

Antall skadedyr økte raskest i $t=\frac{20}{3} \cdot ln(39) \approx 24$ dager etter at huset ble invadert. Dette er vendepunktet til f(t). Da var vekstfarten på 9 skadedyr per dag.

c)

Bruker CAS i Geogebra til å løse oppgaven.

Det hadde vært skadedyr i ca. 35 dager da huset ble kontrollert. Denne oppgaven kan også løses grafisk.