S1 2018 vår LØSNING

oppgaven som pdf

Løsning laget av mattepratbruker Tommy O.

Løsning laget av LektorNilsen (pdf)

diskusjon av oppgaven på matteprat

Oppgave 1

a)

$2x^2-5x+1=x-3 \\ 2x^2-5x-x+1+3 = 0 \\ 2x^2-6x+4=0 \quad |:2 \\ x^2-3x+2=0$

Bruker abc-formelen $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$, $a=1$, $b=-3$, $c=2$.

$x=\frac{-(-3)\pm\sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot1} \\ x=\frac{3\pm\sqrt{1}}{2} \\ x_1=\frac{3-1}{2} \vee x_2=\frac{3+1}{2} \\ x_1=1 \vee x_2=2$

b)

$2lg(x+7)=4 \quad |:2\\ lg(x+7)=2 \\ 10^{lg(x+7)}=10^2 \\ x+7 = 100 \\ x=93$

c)

$3\cdot2^{3x+2}=12\cdot2^6 \quad |:3 \\ 2^{3x+2} = 4\cdot 2^6 \quad |:2^6 \\ \frac{2^{3x+2}}{2^6} = 4 \\ 2^{3x+2-6}=4 \\ 2^{3x-4}=2^2 \\ 3x-4=2 \\ 3x=6 \\ x=2$

Oppgave 2

<math> \left[ \begin{align*} x^2 + 3y = 7 \\ 3x - y = 1 \end{align*}\right] </math>

Løser likning to med hensyn på y:

$3x-y=1 \\ 3x-1=y \\ y=3x-1$

Bruker innsettingsmetoden og erstatter y med 3x-1 i likning én.

$x^2+3(3x-1) = 7 \\ x^2+9x-3-7=0 \\ x^2 +9x-10=0$

Bruker abc-formelen $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$, $a=1$, $b=9$, $c=-10$.

$x=\frac{-9\pm\sqrt{(9)^2-4\cdot 1 \cdot (-10)}}{2\cdot1} \\ x=\frac{-9\pm\sqrt{121}}{2} \\ x_1=\frac{-9-11}{2} \vee x_2=\frac{-9+11}{2} \\ x_1=-10 \vee x_2=1$

Bruker likning to for å finne tilhørende y-verdier:

$y=3x-1 \\ y_1=3\cdot (-10)-1 \quad \vee \quad y_2=3\cdot 1 - 1 \\ y_1=-31 \quad \vee \quad y_2=2$

Løsning: $x_1=-10 \wedge y_1=-31 \quad \vee \quad x_2=1 \wedge y_2=2 $

Oppgave 3

a)

$(2x-3)^2-2x(2x-6)\\=(2x)^2-2\cdot2x\cdot3+3^2-2x\cdot2x-2x\cdot(-6)\\=4x^2-12x+9-4x^2+12x\\=9$

b)

$lg(2a)+lg(4a)+lg(8a)-lg(16a)\\=lg(\frac{2a\cdot4a\cdot8a}{16a})\\=lg(4a^2)\\=lg(2a)^2\\=2lg(2a)$

c)

$\frac{1}{a}+\frac{1}{b}-\frac{a-b}{ab}\\=\frac{1\cdot b}{a\cdot b}+\frac{1\cdot a}{a\cdot b}-\frac{a-b}{ab}\\=\frac{b}{ab}+\frac{a}{ab}-\frac{a-b}{ab}\\=\frac{b+a-a+b}{ab}\\=\frac{2b}{ab}\\=\frac{2}{a}$

Oppgave 4

Kjenner igjen likningen $x^2-3x+2=0$ fra oppgave 1a). Løsningen var $x_1=1$ og $x_2=2$.

Et andregradsuttrykk $ax^2+bx+c$ med nullpunkter $x_1$ og $x_2$ kan faktoriseres slik: $ax^2+bx+c=a(x-x_1)(x-x_2)$

Faktoriserer uttrykket: $x^2-3x+2=(x-1)(x-2)$

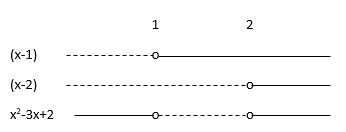
Lager fortegnsskjema:

Løsning: $x^2-3x+2\geq0$ når $x\leq1 \wedge x\geq2$

Oppgave 5

a)

b)

Bruker hypergeometrisk sannynlighet, og leser av binomialkoeffisientene i Pascals trekant. (Eksempel: $\binom{7}{3}$ finner du i rad nr.7 og tall nr.3 i raden. Husk å begynne å telle på rad nr.0 og tall nr.0. Hvis du har talt riktig finner du at $\binom{7}{3}=35$).

P(tre blå kuler)=$\frac{\binom{4}{3}\cdot \binom{3}{0}}{\binom{7}{3}}=\frac{4\cdot1}{35}=\frac{4}{35}$

Sannsynligheten for at du trekker 3 blå kuler er $\frac{4}{35}$.

c)

Dersom du skal trekke både røde og blå kuler, må du trekke enten én blå og to røde, eller to blå og én rød.

P(både røde og blå kuler) = P(én blå og to røde)+P(to blå og én rød)

$=\frac{\binom{4}{1}\cdot\binom{3}{2}}{\binom{7}{3}}+\frac{\binom{4}{2}\cdot\binom{3}{1}}{\binom{7}{3}}\\=\frac{4\cdot3}{35}+\frac{6\cdot3}{35}\\=\frac{12+18}{35}\\=\frac{30}{35}\\=\frac{6}{7}$

Sannsynligheten for at du trekker både røde og blå kuler er $\frac{6}{7}$

Oppgave 6

Uttrykker de to siste ulikhetene med hensyn på y:

Ulikhet nr. 3: $x+y\leq 10 \\ y \leq -x+10$

Ulikhet nr. 4: $3x-2y \leq -2 \\ -2y \leq -3x - 2 \quad |:(-2) \\y \geq 1,5x + 1$

NB: husk å snu ulikhetstegnet når du ganger eller deler en ulikhet med et negativt tall.

Vi har nå de fire ulikhetene:

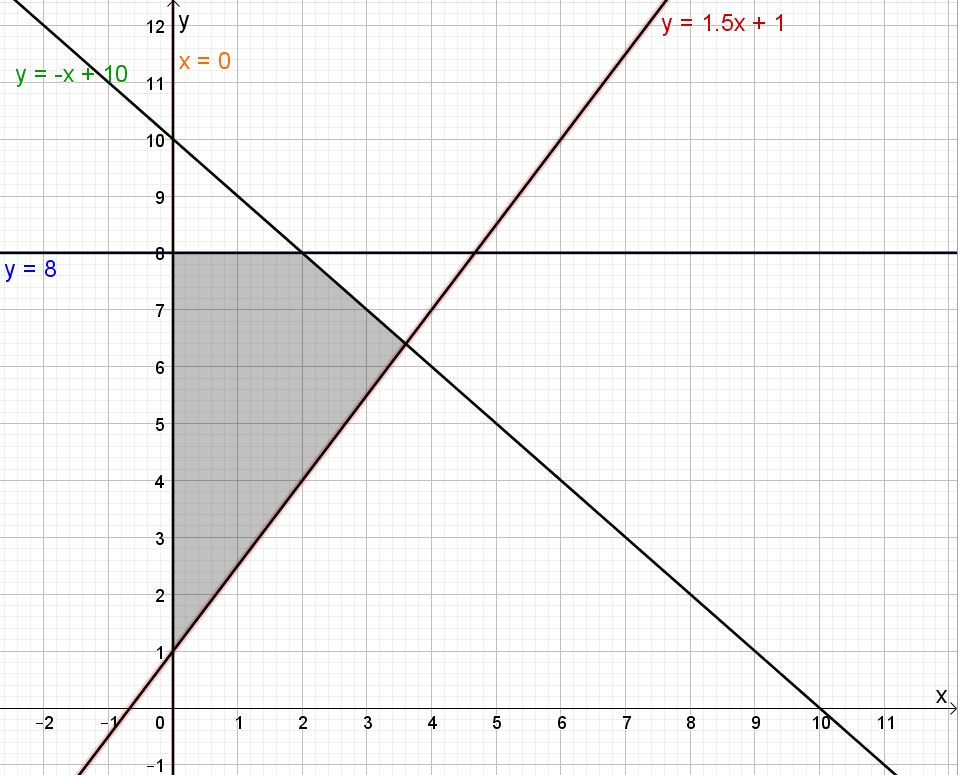
$x\geq0 \\ y\leq 8 \\ y \leq -x+10 \\ y \geq 1,5x + 1$

Tegn de fire linjene $x=0,\,y=8,\,y=-x+10,\,y=1.5x+1$ (for hånd siden det er del 1). Legg godt merke til hvilken vei ulikhetstegnet er i de fire ulikhetene, og skraver området som avgrenses av disse.

Oppgave 7

a)

$f(x)=\frac{2x-1}{x+2} \quad , \quad x\neq -2$

Finner vertikal asymptote, som er den x-verdien som gir null i nevner, i dette tilfellet $x=-2$.

Finner horisontal asymptote ved å la x gå mot uendelig.

$$y=\lim_{x\to\infty} \frac{2x-1}{x+2} \approx \lim_{x\to\infty} \frac{2x}{x}=2$$

Finner nullpunktet (dvs. skjæringspunktet med x-aksen):

$\frac{2x-1}{x+2}=0 \quad | \cdot(x+2) \\ 2x-1=0 \\ x=\frac{1}{2}$

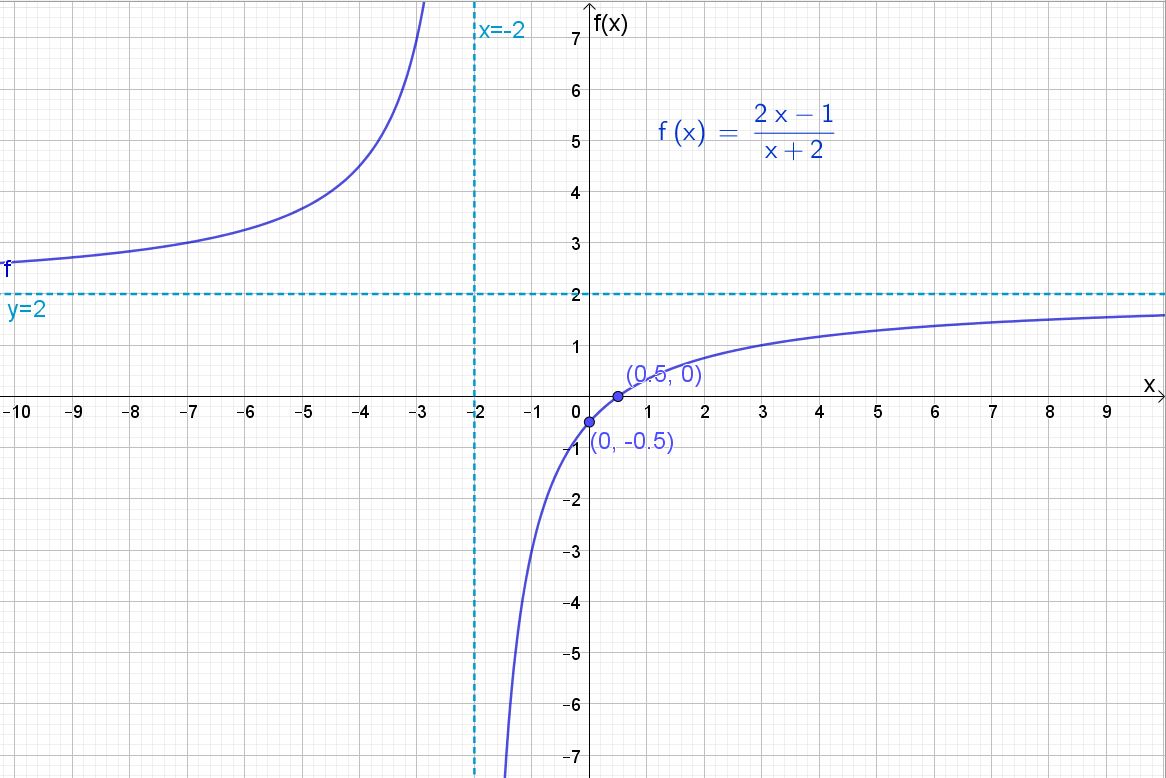
Finner skjæringspunktet med y-aksen, som er det samme som konstantleddet, i dette tilfellet $y= - \frac{1}{2}$

Skisserer grafen (du må gjøre det for hånd):

b)

Setter $f(x)=x-2$:

$\frac{2x-1}{x+2}=x-2 \quad | \cdot(x+2) \\ 2x-1=(x-2)(x+2) \\ 2x-1=x^2-2^2$ (konjugatsetningen) $\\ -x^2+2x+3=0 \\ x= \frac{-2 \pm \sqrt{2^2-4\cdot (-1) \cdot 3}}{2\cdot(-1)} \\ x= \frac{-2\pm \sqrt{4+12}}{-2} \\ x_1= \frac{-2+4}{-2} \quad \wedge \quad x_2=\frac{-2-4}{-2} \\ x_1=-1 \quad \wedge \quad x_2=3$