2PY 2018 vår LØSNING: Forskjell mellom sideversjoner
| Linje 58: | Linje 58: | ||
Formel for antall sekskanter: $(n-1)$ | Formel for antall sekskanter: $(n-1)$ | ||
Antall sekskanter i figur nr. 42: $42-1 = 41$ | Antall sekskanter i figur nr. 42: $42-1 = 41$ | ||
Sideversjonen fra 23. mai 2018 kl. 12:47
- Løsningsforslag (pdf) fra joes. Send gjerne en melding hvis du oppdager feil i akkurat dette løsningsforslaget. På forhånd, takk.
- Løsningsforslag eksamen 2PY V18 (pdf) laget av Jon Bjarne Bø.
DEL EN
Oppgave 1
Variasjonsbredde: $30-(-24) = 30 + 24 = 54$ poeng
Gjennomsnitt: $\frac{20-15+5+15-8-3-24+30}{8} = \frac{20}{8} = \frac{5}{2} = 2,5 $ poeng
Oppgave 2
$\frac{20}{100} \cdot 25 = \frac{500}{100} = 5 $
5 elever i klassen til Mats har bodd i Norge i mindre enn fire år.
Oppgave 3
$\frac{5 \cdot 10^6}{2 \cdot 10^{-8}} = \frac{5}{2} \cdot 10^{6-(-8)} = 2,5 \cdot 10^{14} $
Oppgave 4
a)
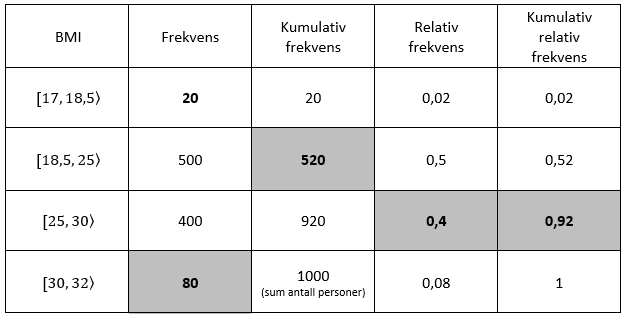
b)
80 personer har fedme.
520 personer er undervektige eller normalvektige.
40% av personene er overvektige.
92% av personene er undervektige, normalvektige eller overvektige.
c)
Medianen er vekten til personen mellom nr. 500 og 501 (siden det er 1000 personer med i undersøkelsen), og vi ser i den kumulative frekvensen at denne personen befinner seg i klassen for normalvektige.
Oppgave 5
a)
b)
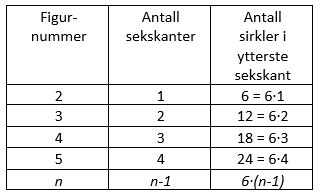
Antall sirkler i ytterste sekskant er 246. Vi finner figurnummeret, n:
$6 \cdot (n-1) = 246 \\ n-1 = \frac{246}{6} \\ n-1 = 41 \\ n = 41 + 1 \\ n = 42$
Nå som vi vet figurnummeret kan vi finne antall sekskanter i figur nr. 42:
Formel for antall sekskanter: $(n-1)$
Antall sekskanter i figur nr. 42: $42-1 = 41$
Det er 41 sekskanter i figuren.