Brøkregning: Forskjell mellom sideversjoner
| Linje 20: | Linje 20: | ||
Vi sammenlikner Per med Pål: $\frac 46 = \frac 23$. Per fikk to trededeler så mange fisk som Pål. | Vi sammenlikner Per med Pål: $\frac 46 = \frac 23$. Per fikk to trededeler så mange fisk som Pål. | ||
Vi sammenlikner Pål med Per: $\frac 64$ = \frac 3/2 Pål fikk 3/2 så mye fisk som Per. Legg merke til at det vi sammenligner mot alltid skal i teller. | Vi sammenlikner Pål med Per: $\frac 64$ = \frac 3/2$ Pål fikk 3/2 så mye fisk som Per. Legg merke til at det vi sammenligner mot alltid skal i teller. | ||
'''Brøk kan brukes til å sammenlikne mengder eller størrelser.''' | '''Brøk kan brukes til å sammenlikne mengder eller størrelser.''' | ||
Sideversjonen fra 11. feb. 2018 kl. 13:01
Innledning
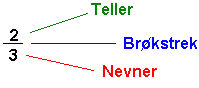
En brøk består av tre elementer, teller, brøkstrek og nevner.
Brøkstrek betyr det samme som deletegn. En brøk er en del av noe. Hvor stor del kommer an på teller og nevner. Nevneren forteller hvor mange deler helheten er delt opp i.
Hvorfor trenger vi brøk?
- Vi har tall som er mindre enn en enhet. En halv liter melk forteller noe om mengden i forhold til enheten liter melk. En brøk kan angi en del av noe.
- Når vi deler et tall på et annet kan vi få et svar som blir mindre enn en:
$10 :30 = \frac {10}{30} = \frac 13$ En brøk kan være svaret på et delestykke.
Svaret over er pent og helt nøyaktig. Dersom du bruker kalkulator får du 0,333333.... som ikke er pent og ikke helt nøyaktig.
- Sammenlikning av størrelser eller mengder. Per fikk 4 fisk og Pål fikk 6 fisk. Her må vi tenke om vi skal sammenlikne Per med Pål, eller Pål med Per..
Vi sammenlikner Per med Pål: $\frac 46 = \frac 23$. Per fikk to trededeler så mange fisk som Pål.
Vi sammenlikner Pål med Per: $\frac 64$ = \frac 3/2$ Pål fikk 3/2 så mye fisk som Per. Legg merke til at det vi sammenligner mot alltid skal i teller. Brøk kan brukes til å sammenlikne mengder eller størrelser.
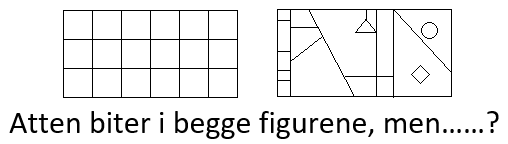
Man må dele i LIKE STORE BITER.
Figuren til venstre kan representere en brøk fordi alle bitene er like store. Dersom to personer får en bit hver har begge fått like mye, $\frac{1}{18}$.
Figuren til høyre består også av atten biter, men her er bitene av forskjellig størrelse. Denne figuren kan ikke brukes til å representere en brøk. Dersom to personer får en bit hver har de trolig fått forskjellig andel (mengde) av figuren.
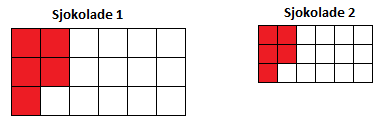
Dersom man får 5 biter sjokalade av sjokolade 1 har man fått $\frac{5}{18}$ av sjokolade 1. Dersom man får 5 biter av sjokolade 2 har man fått $\frac{5}{18}$ av sjokolade 2. Brøkene er de samme, men vi observerer at den som har fått fra sjokolade 1 får mest sjokolade fordi sjokolade 1 er større. Dersom to personer får 5 deler hver, fra samme sjokolade, får de like mye begge to.
Deler du en pizza i fire like store biter blir nevneren fire. Spiser du en av bitene har du spist 1/4 av pizzaen. Telleren sier altså noe om hvor mange av delene i nevneren som "er med på leken".
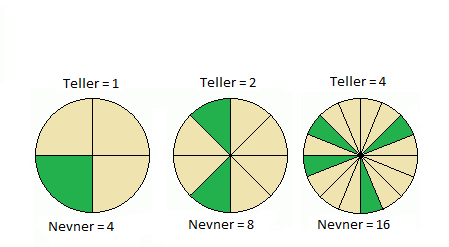
grønn er teller, grønn + grå er nevner
Deler du samme pizza opp i åtte like stykker blir stykkene havparten så store som når du deler den i fire. Om du spiser to stykker når pizzaen er delt i åtte, er det likeverdig med å spise et stykke når pizzaen er delt i fire. Slik kan vi fortsett. Det kalles å utvide brøken.
Å utvide brøken
Om vi holder oss til eksempelet over kan vi skrive det slik:
<math> \frac{1}{4} = \frac{2}{8} = \frac{4}{16}</math>
Det vi egentlig gjør er å multiplisere teller og nevner med samme tall, i dette tilfellet 2.
<math> \frac{1}{4} = \frac{1 \cdot 2}{4 \cdot 2} = \frac{2}{8} = \frac{2 \cdot 2}{8 \cdot 2}= \frac{4}{16}</math>
Vi kan utvide en brøk med både tall og bokstaver, men det er viktig at vi gjør det samme i både teller og nevner. Gjør vi ikke det, vil brøkens verdi endre seg.
Å forkorte brøken
Å forkorte en brøk er det motsatte av å utvide den. Først må vi faktorisere teller og nevner. Se siden om faktorisering dersom du ikke kan det.
Brøken tolv sekstendeler kan skrives som:
<math> \frac{12}{16} = \frac {2 \cdot 2 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 2} = \frac{3}{4}</math>Når vi forkorter 2- tallene i teller og nevner må vi huske på at de erstattes med tallet 1. De går ikke an å få null i teller eller nevner når vi forkorter på denne måten. Også her er det viktig at vi gjør det samme i både teller og nevner.
Blandet tall eller "uekte brøk"
Et blandet tall består av et heletall og en brøk. En uekte brøk er ekte nok, betegnelsen brukes om brøker som er større enn en. Det betyr at teller er større enn nevner.
Eks: $ 1\frac14 $
Dette blandede tallet består av en hel og en fjerdedel. Det kan illustreres med figuren over.
Addisjon og subtraksjon
Når nevner er den samme
Når nevneren i to eller flere brøker skal trekkes sammen legger vi sammen tellerene (eller trekker fra), og beholder nevneren slik den er.
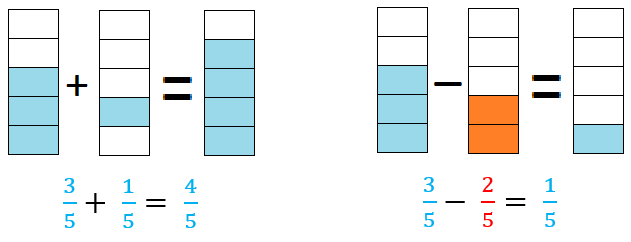
<math> \frac 27 + \frac 37 = \frac{2+3}{7}= \frac 57 </math>
<math> \frac 35 - \frac 25 = \frac{3-2}{5}= \frac 15 </math>
Når nevner er forskjellig
Når man skal legge sammen eller trekke fra to eller flere brøker med forskjellig nevner, må man først finne fellesnevner.
<math>\frac 13 + \frac 12 = \frac{1 \cdot 2}{3 \cdot 2}+ \frac {1 \cdot 3}{2 \cdot 3 } = \frac 26 + \frac {3}{6} = \frac 56 </math>
Vi finner nevnerens minste felles multiplum (mfm), det minste tallet som begge nevnerene går opp i. Det minste tallet både to og tre går opp i er seks. Dette er et eksempel på nødvendigheten av å kunne utvide brøker.
Multiplikasjon
Brøk med brøk
Når to brøker skal multipliseres (ganges) med hverandre, multipliserer vi teller med teller og nevner med nevner.
Heltall med brøk
Vi multipliserer heltallet i teller og beholder nevner.
Divisjon
Når to brøker skal divideres (deles) med hverandre, snur vi den siste brøken (divisor) og multipliserer utrykket. Med snu menes at vi bytter om teller og nevner. Eks:
Hvorfor er det slik? La oss se på et eksempel til:
Man obserever at metoden i eksempelet over er mye enklere. Dette eksemplet er bare ment som en forklaring på hvorfor man kan "snu" den siste brøken og gange.
Divisjon med brøk og heltall
Man løser problemet ved å gjøre heltallet om til brøk, og bruker regelen over.
Null i teller
Dersom telleren er null er brøkens verdi lik null.
<math> \frac 01 = \frac 02 = \frac 03 = ..... = \frac 0n = 0</math>
Der n er forskjellig fra null.
Null i nevner
Det er ikke mulig å få null i nevneren til en brøk. Dersom du har fått det har du regnet feil.
Teller og nevner like store
Når teller og nevner er like store er brøkens verdi lik en.
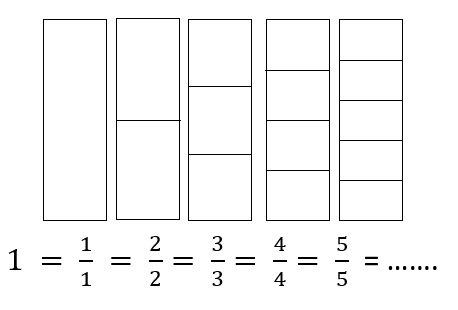
<math> \frac 11 = \frac 22 = \frac 33 = ..... = \frac nn = 1</math>
Der n er forskjellig fra null.
Fra heltall til brøk
Et hvilket som helst heltall kan gjøres om til en brøk med en hvilken som helst nevner.
Et heltall gjøres om til brøk slik: <math>1= \frac 11 = \frac22 = \frac33 = ...... </math>
Eller slik:
<math>4= \frac 41 = \frac82 = \frac{12}{3} = ...... </math>
Du skriver fire som fire endeler. Så utvider du brøken slik at du får den nevneren du ønsker. Ønsker du brøken i syvdeler multipliserer du både fire og en med syv og får $\frac{28}{7}$.