1T 2016 høst LØSNING: Forskjell mellom sideversjoner
m →b): Feil utregning i siste ledd. Endret fra 4*pi*a^2 til pi*a^2 |
|||
| Linje 242: | Linje 242: | ||
$A= (\frac{\pi (\frac 52a)^2}{2}) -(\frac{\pi (\frac12)^2}{2}) -(\frac{ \pi (2a)^2}{2})\ A = (\frac{\pi a^2}{2} )((\frac52)^2 - (\frac 12)^2 - 2^2) \ A= | |||
==DEL TO== | ==DEL TO== | ||
Sideversjonen fra 17. nov. 2017 kl. 14:02
Diskusjon av denne oppgaven på matteprat
DEL EN
Oppgave 1
Tar utgangspunkt i likning #2 og lager først et uttrykk for y
Setter det inn i likning #1
Setter så inn verdien for x inn i hvilken som helst vilkårlig likning, i dette tilfellet tar vi for oss likning 1 fordi den er enklest.
Derfor,
Oppgave 2
Først omskriver vi det litt med hensyn til faktorisering.
Ser vi i nevneren vil vi se at vi har et andregradsuttrykk. Dette kan du faktorisere ved hjelp av abc-formelen.
Du finner fort ut at likninga kun har ett nullpunkt for
videre får du
Oppgave 3
Faktoriserer uttrykket:
Gir oss uttrykket på faktorisert form:
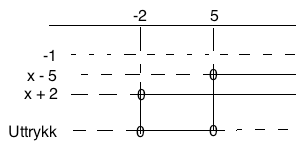
Tegner så fortegnsskjema.
Oppgave 4
Ved hjelp av logaritmereglene vet vi at
Derfor kan vi si at
Ved hjelp av denne logaritmeregelen
Kan vi si at
Oppgave 5
Vi kjenner til regelen
Derfor får vi at
Vi kjenner regelen
Derfor kan vi si at
Oppgave 6
Oppgave 7
Oppgave 8
Parabler er på formen
Vi ser at f(0)= - 4, dvs c= -4
Vi har nullpunktene:
a(x - 4)(x + 2) og velger et punkt på grafen (0, -4):
Vi mangler nå b og velger feks punktet (4,0):
Funksjonen er gitt ved uttrykket
Oppgave 9
a
Alle tre faktorene vil bli lik null som gir
b
c
Vi finner topp og bunnpunkter når den deriverte = 0, dvs. ved 0 vekst.
Vi vet derfor at funksjonen har et ekstremalpunkt i
d
Først finner vi stigningstallet
Så finner vi likningen
e)
Dersom vi skal ha flere tangenter parallell med den i i d), må likningen
Det finnes ingen andre tangenter parallell med den i d).
Oppgave 10
Hver av sidene har lengde 8.
Høyden i trekanten blir et katet i en trekant der det andre katetet er 4 og hypotenus 8. Lengden blir da
Arealet av trekanten blir
Oppgave 11
Oppgave 12
a)
Hvilket skulle vises.
b)
Oppgave 13
a)
P( BRR) =
b)
Det er tre posisjoner for blå nisse: P( en blå og to røde)
c)
Dersom vi IKKE har minst en blå har vi tre røde. Sannsynligheten for det er:
P( bare røde)=
Sannsynligheten for minst en blå blir da:
P( minst en rød) =
Oppgave 14
a)
Omkretsen av det blå området er lik summen av periferiene av de tre halvsirklene.
Omkretsen er fem ganger a ganger pi.
b)
Arealet av det blå området er arealet av den store halvsirkelen, minus arealene av de to små halvsirklene.
DEL TO
Oppgave 1
a)
b)
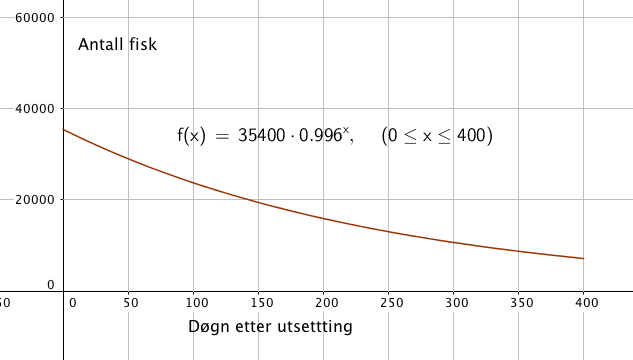
35 400 er antall fisk som blir satt ut, altså startverdien.
0,996 er vekstfaktoren. Den forteller om endring i prosent per tidsenhet. I dette tilfelle er vekstfaktoren mindre enn en, da har vi prosentvis reduksjon.
Reduksjonen er 0,004 som er 0,4% reduksjon per døgn.
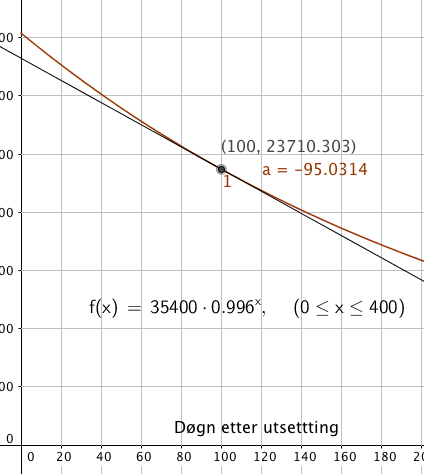
c)
Døgn nr. 100 dør det ca. 95 settefisk.
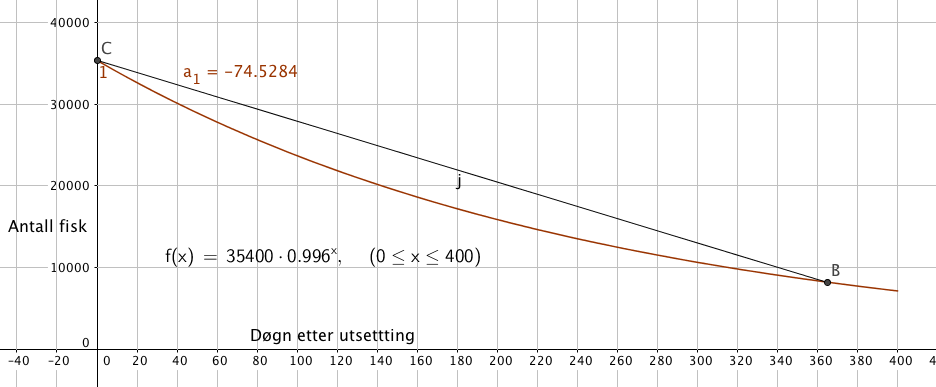
d)
Det første året dør det i gjennomsnitt 74,5 fisk hvert eneste døgn.
Oppgave 2
a)
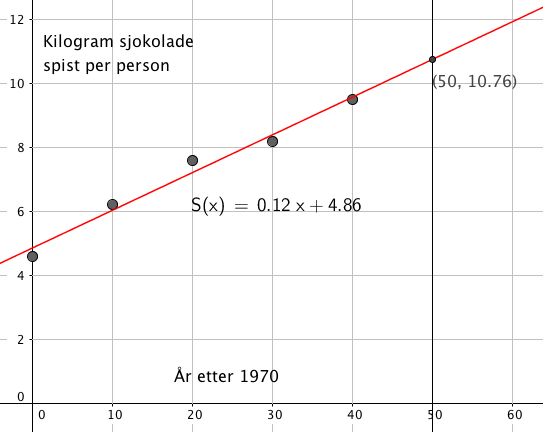
b)
Det foteller at vi spiser ca. 120 gram MER sjokokolade for hvert år som går.
c)
Da kommer vi i følge modellen til å spise ca. 10,8 kg. sjokolade.
Oppgave 3
a)
Stigningstallet til en rett linje :
b)
Skjæring med x akse:
Skjæring med y akse:
Oppgave 4
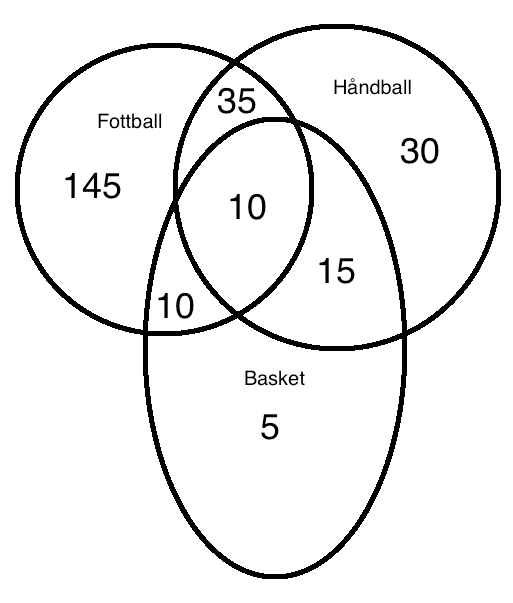
a)
Basketball og håndball er: 90 - 30 - 35 - 10 = 15
160 medlemmer spiller bare fotball og / eller basketball. Det betyr at 10 gjør begge deler:
b)
Det er fire prosent sannsynlighet for å velge en som driver med alle tre idrettene.
c)
Det er 50% sannsynlighet for at en som driver med håndball også spiller fotball.
Oppgave 5
Detter er en dobbeltrot og fortegnet blir likt på begge sider av a, men null for x = a, derfor terassepunkt.
Oppgave 6
a)
Bruker Pytagoras på BCD, 30, 60 90.
b)
Nedfeller normalen fra D på AB. Figuren består da av rektangelet BCDE og den likebeinte og rettvinklede trekanten AED.
Areal trekant:
Areal rektangel:
Areal ABCD: