S1 2016 høst LØSNING

Oppgaven som pdf

Diskusjon og delvis løsning av denne oppgaven

Oppgave 1

A)

$\frac{2x-1}{3}-\frac{3x+2}{4}=\frac{5}{6}\\ (\frac{2x-1}{3}*12)-(\frac{3x+2}{4}*12)=(\frac{5}{6}*12)\\ 8x-4-9x-6=10\\ x=-20$

B)

$lg(2x-6)=2\\10^{lg(2x-6)}=10^{2}\\2x-6=100\\x=53$

Oppgave 2

A)

$a(a-b)+b(b-a)\\a^{2}-ab+b^{2}-ab\\a^{2}-2ab+b^{2}\\(a-b)^{2}$

Begge løsningene av de to nederste radene gir full uttelling, henvist til sensorveiledningen.

B)

$\frac{(ab^2)^2b^-3}{a^2(b^-1)^2}\\a^{(2-2)}*b^{(4-3+2)}\\b^{3}$

C)

$lg2+lg4+lg9-lg3-lg8\\lg2+2lg2+2lg3-lg3-3lg2\\lg3$

Oppgave 3

A)

Setter opp to likninger:

$L1: x+y=200\\L1: y=200-x$

Dagen etter hadde de 110 kroner igjen tilsammen:

$L2: (x-\frac{1}{2}x)+(y-10)=110$

B)

Setter inn L1 inn i L2 ved hjelp av innsettingsmetoden:

$(x-\frac{1}{2}x)+((200-x)-10)\\(x-\frac{1}{2}x)+(200-x-10)=110\\ \frac{1}{2}x=80\\x=160$

Per hadde 160 kroner på Mandag.

Oppgave 4

$x^2+6≤5x\\x^2-5x+6≤0$

Bruker Abc formelen med x^2-5x+6=0

$x=\frac{5\pm \sqrt{25-24}}{2}\\x=2 \vee x=3$

Setter inn verdier for når x<2, 2<x<3 og x>3 inn i opprinnelige uttrykket for å finne ut hvilke x-verdier som stemmer.

$1^2+6>5*1\\ \frac{5}{2}^2+6<5*\frac{5}{2}\\4^2+6>5*4$

Løsningen blir derfor:

$x^2+6≤5x\Rightarrow2≤x≤3$

Kun løsning av annengradslikningen gir ingen uttelling, henvist til sensorveiledningen.

Oppgave 5

A)

Bruker uordnet uten tilbakelegging:

Dette gir 6!=6*5*4*3*2 mulige utfall.

Billettene kan deles ut på 720 måter.

Oppgave 6

A)

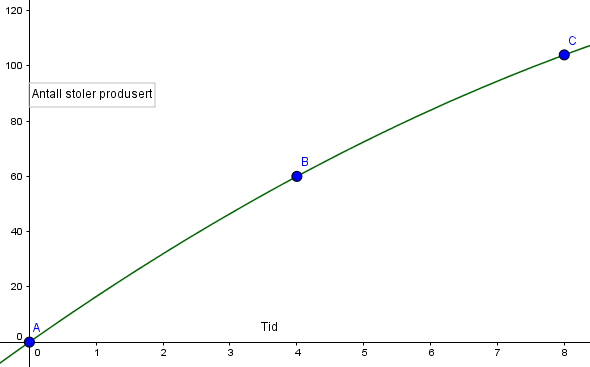
Beregn S(0), S(4) og S(8) for å finne punkter på grafen

Deretter sett inn (0,0), (4,60) og (8,104) og trekk linje igjennom disse.

B)

Bruker formel for gjennomsnittlig veksthastighet:

$\frac{S(4)-S(0)}{4-0}\\ \frac{(17*4-0,5*4^2)-(17*0-0,5*0^2)}{4}\\ 15$

Gjennomsnittlig veksthastighet til S i tidsrommet [0, 4] er 15. I løpet av de fire første timene produserer Per 15 stoler per time i gjennomsnitt på en normal dag.

C)

Deriverer funksjonen og setter den deriverte lik 4:

$S`(4)=-t+17\\-4+17\\13$

Per øker produksjonen med 13 stoler i timen fra fire til fem timer i produksjon.

Må tolke svaret til oppgaven for å få full uttelling, henvist til sensorveiledningen

D)

Regner ut hvor mange stoler han produserer på 4 timer:

$17*4-0,5*4^2\\60$

Tjener 10 kroner per stol han produserer, dette gir 60*10 kroner.

Per tjener 600 kroner på å produsere i 4 timer.

E)

Per tjener 10 kroner per stol og produserer dermed 14 stoler i gjennomsnitt per time. Bruker dermed formelen for gjennomsnittlig veksthastighet og setter denne lik 14:

$\frac{17t-0,5t^2}{t}=14\\0.5t^2=3t\\ t^2=6t\\ \frac{t^2}{t}=6\\t=6$

Kan sjekke svaret ved å sette S(6):

$17*6-0,5*6^2\\102-36\\84\\ \Downarrow\\84*10=840\\ \Downarrow\\ \frac{840}{6}=140$

Per jobbet i seks timer da gjennomsnittlig timelønnen var 140 kroner.