R1 2016 vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| Linje 149: | Linje 149: | ||
==Oppgave 1== | ==Oppgave 1== | ||
===a)=== | |||
===b)=== | |||
===c)=== | |||
==Oppgave 2== | ==Oppgave 2== | ||
Sideversjonen fra 23. mai 2016 kl. 19:26
Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du har kommentarer til løsningsforslaget. På forhånd, takk.
Løsningsforslag (pdf) fra bruker LektorH.
Løsningsforslag (pdf) fra bruker Claves
DEL EN
Oppgave 1
a)
$f(x)=-3x^2+6x-4$
$f'(x)=-6x+6= -6(x-1)$
b)
$g(x)=5\ln(x^3-x)$
$g'(x)=\frac{5(3x^2-1)}{x^3-x}$
c)
$h(x)=\frac{x-1}{x+1}$
$h'(x)=\frac{x+1-(x-1)}{(x+1)^2}=\frac{2}{(x+1)^2}$
Oppgave 2
a)
$p(x)=x^3-7x^2+14x+k$
$p(x)$ er delelig med $(x-2)$ hvis og bare hvis $p(2)=0$
$p(2)=8-7\cdot4+14\cdot2+k=8-28+28+k=8+k$
$8+k=0$
$k=-8$
b)
$ \quad x^3-7x^2+14x-8 :(x-2)= x^2 - 5x + 4 \\ -(x^3-2x^2) \\ \quad \quad-5x^2 + 14x -8 \\ \quad \quad -(-5x^2 -10x) \\ \quad \quad \quad \quad \quad (4x -8)$
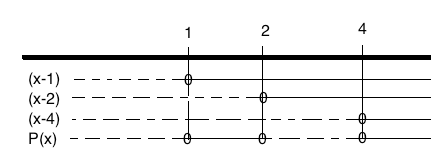
$x= \frac{5 \pm \sqrt{25 - 16}}{2} \\ x= 1 \vee x =4 \\ \\ P(x)= (x-1)(x-2)(x-4)$
c)
$P(x) \leq 0 $
$x \in < \leftarrow,1] \cup [2,4]$
Oppgave 3
a)
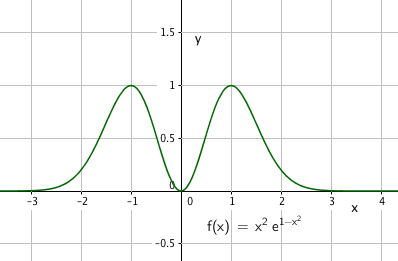
$f(x)=x^2e^{1-x^2}$
$f'(x)=2xe^{1-x^2}+x^2\cdot-2xe^{1-x^2}=2xe^{1-x^2}(1-x^2)$
b)
c)
d)
Oppgave 4
a)
$AB=AC=BC=6 \ cm$
$HB=\frac{1}{2}AB=3 \ cm$
$CH=\sqrt{(BC)^2-(HB)^2}=\sqrt{6^2-3^2} \ cm=\sqrt{27}=\sqrt{3^3} \ cm=3\sqrt{3} \ cm$
$CF=CE=\sqrt{(BC)^2+(BE)^2}=\sqrt{6^2+6^2} \ cm=\sqrt{2\cdot6^2} \ cm=6\sqrt{2} \ cm$
$HF=\sqrt{(CF)^2-(CH)^2}=\sqrt{72-27} \ cm=\sqrt{45} \ cm=\sqrt{9\cdot5} \ cm=3\sqrt{5} \ cm$
b)
$\frac{AF}{AB}=\frac{3+3\sqrt{5}}{6}=\frac{3(1+\sqrt{5})}{2\cdot3}=\frac{1+\sqrt{5}}{2}=\phi$
Oppgave 5
Oppgave 6
a)
Antall mulige fagkombinasjoner med 2 realfag og 2 andre fag:
${5\choose2}\cdot{8\choose2}=\frac{5\cdot4}{2!}\cdot\frac{8\cdot7}{2!}=10\cdot28=280$
b)
Antall mulige fagkombinasjoner med 4 fag hvor minst 2 er realfag:
${5\choose2}\cdot{8\choose2}+{5\choose3}\cdot{8\choose1}+{5\choose4}=280+\frac{5\cdot4\cdot3}{3!}\cdot8+5=280+80+5=365$
Oppgave 7
a)
b)
$f(x)=x^2+px+q$
$A=(0,1)$
$B=(-p,q)$
$\vec{OS}=\vec{OA}+\frac{1}{2}\vec{AB}=[0,1]+\frac{1}{2}[-p,q-1]=[\frac{-p}{2},1+\frac{q-1}{2}]=[\frac{-p}{2},\frac{q+1}{2}]$
$S=(\frac{-p}{2},\frac{q+1}{2})$
$r=|\vec{AS}|=\sqrt{(\frac{-p}{2})^2+(\frac{q-1}{2})^2}=\sqrt{\frac{p^2+(q-1)^2}{4}}=\frac{\sqrt{p^2+(q-1)^2}}{2}$
c)
Likning for sirkel:
$(x-x_1)^2+(y-y_1)^2=r^2$
$(x+\frac{p}{2})^2+(y-\frac{q+1}{2})^2=\frac{p^2+(q-1)^2}{4}$
Skjæring med x-aksen:
$y=0$
$(x+\frac{p}{2})^2+(-\frac{q+1}{2})^2=\frac{p^2+(q-1)^2}{4}$
$(x+\frac{p}{2})^2=\frac{p^2+(q-1)^2}{4}-\frac{(q+1)^2}{4}$
$x+\frac{p}{2}=\frac{\pm \sqrt{p^2-4q}}{2}$
$x=\frac{-p \pm \sqrt{p^2-4q}}{2}$
Nullpunkter til $f(x)$:
$x^2+px+q=0$
$x=\frac{-p \pm \sqrt{p^2-4q}}{2}$
Sirkelen skjærer x-aksen i nullpunktene til $f(x)$.