R1 2014 vår LØSNING

Løsning fra NDLA

løsning som pdf laget av mattepratbruker claves

Diskusjon om denne oppgaven på matteprat

Oppgave 1

a)

$f(x)= ln(x^2+x) \\ f´(x)= \frac{1\cdot ( 2x+1)}{x^2+x} = \frac{2x+1}{x^2+x}$

b)

$g(x)= x \cdot e^x \\ g´(x)= e^x + xe^x = e^x (1+x)$

c)

$h(x)= (x^2+3)^4 \\ h´(x)= 4(x^2+3)^3 \cdot 2x = 8x(x^2+3)^3$

Oppgave 2

a)

$P(x)= x^3-7x^2+14x-8 $

En går opp i -8, og P(1) = 1 - 7 + 14 -8 = 0.

P har et nullpunkt for x = 1

Oppgave 3

a)

$-2 \vec a + \vec b= -2[-2,1] + [3,6] = [4, -2] + [3,6] = [7, 4] $

Skalarprodukt:

$ \vec a \cdot \vec b = [-2,1]\cdot[3,6] = -6 + 6 =0$

b)

$\vec b || \vec c \\ s[3,6] = [k-1, 4] \\ s = \frac 23 \wedge k = 3$

c)

k slik at $| \vec c| = |2 \vec a| \\ \sqrt{(k-1)^2 + 16} = \sqrt{16+ 4} \\ (k-1)^2 = 4 \\ k-1 = \pm 2 \\ k= -1 \vee k = 3$

Oppgave 4

a)

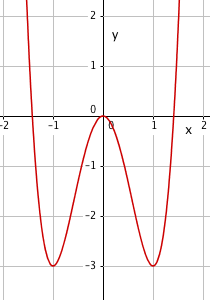
$f(x)= 3x^4-6x^2 = 3x^2(x^2-3) \\ f(x)=0 \\ x=0 \vee x= - \sqrt 3 \vee x = \sqrt 3$

b)

$f´(x) = 12x^3-12x = 12x(x^2-1)$

Vi ser at f har ekstremalpunkter for x = 0 og for $x = \pm 1$

f(0) = 0 , dette er også et nullpunkt.

f( -1) = f( 1) = -3

Da må (0,0) vare et maksimumspunkt, og (-1, -3) og (1, -3) er minimumspunkter (kan se det uten fortegsnsskjema, siden (0,0) også er et nullpunkt).

c)

Oppgave 5

Trekanten ABS er likebeint. Vinkel BAS er 27 grader. Vinkel S er 180 - 54 = 126 grader. S er en sentralvinkel. Vinkelen ACB er en pereferivinkel som spenner over samme bue som S og er derfor 63 grader.

Oppgave 6

a)

p er oddetall større enn 1. Både p - 1 og p + 1 vil da være partall. Alle partall er delelige på 2 og kan skrives på formen 2n, der n er et naturlig tall. Derfor vil

$ \frac{p+1}{2} \wedge \frac{p -1}{2}$ være hele tall.

b)

$( \frac{p+1}{2})^2 - ( \frac{p-1}{2})^2 = (\frac{p+1+p-1}{2})( \frac{p+1-p+1}{2}) =p$

$( \frac{151+1}{2})^2 - ( \frac{151-1}{2})^2 = 76^2 - 75^2$

Oppgave 7

a)

$H(x)=x^x \quad x>0 \\ h(x)= (e^{lnx})^x = e^{x lnx}$

(sjekk potensreglene)

b)

$h´(x) = (e^{u})´\cdot u´\\ h´(x) = e^{x lnx}(lnx + \frac 1x \cdot x) = x^x(lnx +1)$

Oppgave 2

a)

Hypergeometrisk situasjon:

$\frac{\binom{12}{1} \binom{16}{4}}{\binom{28}{5}} = 0,222$

Det er 22,2% sannsynlig at ekkurat en gutt blir med i gruppen.

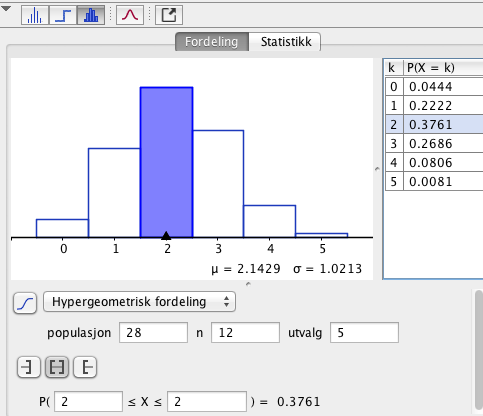
b)

Løser denne enklest med sannsynlighetskalkulatoren i Geogebra. $\frac{44}{117} \approx 0,3716$

Det blir med to gutter.

c)

Vi vet at Betsy er med. Fortsatt hypergeometrisk situasjon. Det er det 27 elever igjen, fire skal trekkes, en av dem skal være Arne:

$\frac{\binom{1}{1} \binom{26}{3}}{\binom{27}{4}} = 0,1481$

Det er 14,8% sannsynlig at Arne også blir med.

Oppgave 3

b)

c)

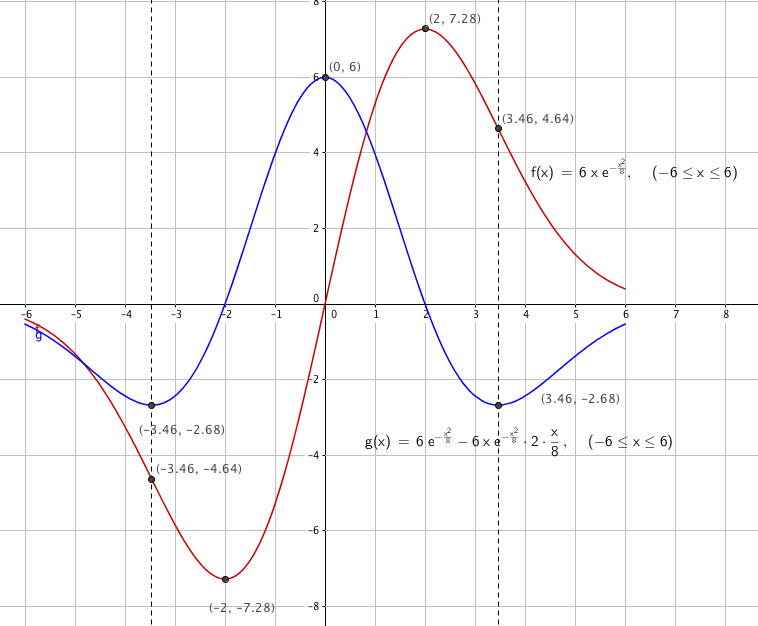
Den deriverte til f(x), g(x) er null for x = -2 og for x = 2. Det betyr at disse er ekstremalpunkter. Fra grafen ser vi at f ha et minimumspunkt for i ( -2, -7.28), og et maksimumspunkt i (2, 7.28). Tilgi meg for å ha brukt en fornuftig, men etter norsk standard feil desimalnotasjon.

Vendepunktene til f finner vi der den derivertetil f, g har ekstremalpunkter, x= -3,46, x= 0 og x= 3,46, noe som gir følgene vendepunkter:

(-3.46, -4.46) fra hul siden ned til opp,

(0,0) fra hul side opp til ned, og

(3.46, 4.46) fra hul side ned til opp.

Oppgave 4

a)

Benevningen er desimeter, dm, i resten av oppgaven er benevninger utelatt.

Overdlaten av boksen består av en bunn med areal $x^2$ og fire sideflater med arealet $xh$. Overflaten blir da $x^2+ 4xh$, og siden det samlede areale skal være 12 får vi:

$x^2+4xh=12$

Uttrykk for h:

$x^2+4xh=12 \\ 4xh= 12-x^2 \\ h = \frac{12-x^2}{4x} \\ h=\frac{3}{x} - \frac{x}{4}$

b)

$x^2$ må være større enn null og mindre enn tolv, dvs $0<x< \sqrt {12}$.

c)

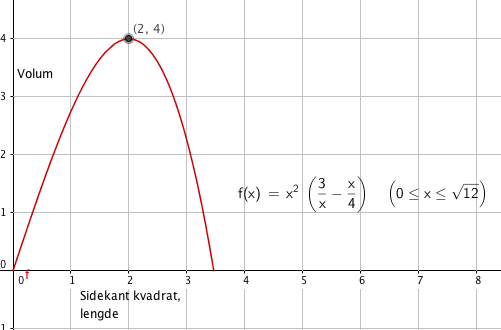
Det spørres ikke om grafen over, men det kan være greit å se hvordan ting ser ut...

Volum av kar: $V(x) = x^2h= x^2( \frac 3x - \frac x4) = 3x - \frac{x^3}{4}$

d)

$V´(x)= 3 - \frac 34x^2 \\ V´(x)=0 \\ 3- \frac 34 x^2 =0 \\ x = \pm 2$

Bruker den positive verdien for x og finner at V(2) = 4. Siden alle mål var i dm. tilsvarer dette 4 liter.

Oppgave 5

a)

Ballen treffer bakken når y-koordinaten til posisjonsvektoren er null: $15-4,9t^2 =0 \\ t^2 = \frac{15}{4,9} \\t = \pm 1,75$

Den trefffer bakken etter 1,75 sekunder.

Oppgave 6

a)

$n^n \cdot ( \frac xn)^{lgx} = x^n \\ ( \frac xn)^{lgx} = ( \frac xn)^n \\ lg ( \frac xn)^{lgx} = lg ( \frac xn)^n$

b)

$ lg ( \frac xn)^{lgx} = lg ( \frac xn)^n \\ lgx( lgx - lg n) = n(lgx - lg n) \\ lgx(lgx - lgn) - n(lgx-lgn)=0 \\ (lgx - n)( lgx - lgn)=0$

c)

$lgx - n =0 \\ lgx =n \\ x= 10^n$

eller

$lgx - lgn = 0 \\ x = n$