Integrasjon: Forskjell mellom sideversjoner
Fra Matematikk.net
Ny side: Integrasjon er en operasjon som tar en funksjon og gir en ny funksjon som beskriver arealet under den første funksjonen. ==Ubestemt integrasjon== Først skal vi vise sammenhengen mellom ... |
Ingen redigeringsforklaring |
||
| Linje 1: | Linje 1: | ||
Integrasjon er en operasjon som tar en funksjon og gir en ny funksjon som beskriver arealet under den første funksjonen. | Integrasjon er en operasjon som tar en funksjon og gir en ny funksjon som beskriver arealet under den første funksjonen. | ||
==Det bestemte integralet== | |||
==Ubestemt integrasjon== | ==Ubestemt integrasjon== | ||
| Linje 36: | Linje 38: | ||
der <tex>\frac{d}{dx}F(x)=f(x)</tex> og <tex>F(a)-F(b)</tex> er lik arealet mellom <tex>x</tex>-aksen og funksjonen <tex>f(x)</tex> mellom <tex>x=a</tex> og <tex>x=b</tex>. | der <tex>\frac{d}{dx}F(x)=f(x)</tex> og <tex>F(a)-F(b)</tex> er lik arealet mellom <tex>x</tex>-aksen og funksjonen <tex>f(x)</tex> mellom <tex>x=a</tex> og <tex>x=b</tex>. | ||
==Integrasjon ved variabelskifte== | |||
==Delvis integrasjon== | |||
Sideversjonen fra 24. jan. 2010 kl. 17:15
Integrasjon er en operasjon som tar en funksjon og gir en ny funksjon som beskriver arealet under den første funksjonen.
Det bestemte integralet
Ubestemt integrasjon
Først skal vi vise sammenhengen mellom integrasjon og derivasjon:
- Bevis: Den deriverte av den integrerte er funksjonen selv
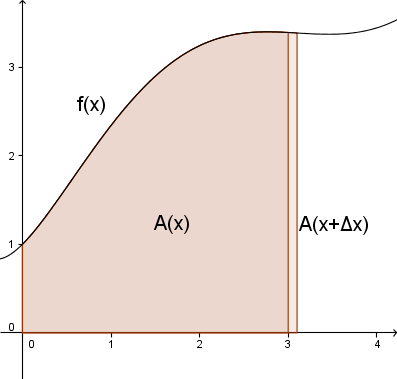
- La <tex>f(x)</tex> være en reell funksjon <tex>(f(x)\in\mathbb{R}\,\forall\, x\in \mathbb{R})</tex>, og la funksjonen <tex>A(x)</tex> beskrive arealet mellom <tex>x</tex>-aksen og <tex>f(x)</tex> ved at <tex>A(b)-A(a)</tex> er lik arealet mellom <tex>x</tex>-aksen og <tex>f(x)</tex> mellom <tex>x=a</tex> og <tex>x=b</tex>. Mellom <tex>x</tex> og <tex>x+\Delta x</tex> vil aralet altså være <tex>A(x+\Delta x)-A(x)</tex>, se figur:
- I grenseverdien når <tex>\Delta x\to 0</tex> vil dette arealet bli tilnærmet et rektangel. Arealet av et rektangel er gitt ved
- <tex>A=l\cdot b</tex>
- og arealet at dette rektangelet ser vi ut ifra figuren blir <tex>f(x)\cdot \Delta x</tex>. Dermed kan vi konkludere at
- <tex>f(x)=\lim_{\Delta x\to0}\frac{A(x+\Delta x)-A(x)}{\Delta x}</tex>
- Men dette kjenner vi som definisjonen av den deriverte. Altså kan vi skrive at
- <tex>f(x)=\frac{d}{dx}A(x)</tex>
- Vi har dermed bevist at derivasjon og integrasjon er inverse operasjoner av hverandre, det vil si at
- <tex>\frac{d}{dx}\int f(x)dx=f(x)</tex>
Kalkulusens andre fundamentalteorem sier at
<tex>\int_a^b f(x)dx=F(b)-F(a)</tex>
der <tex>\frac{d}{dx}F(x)=f(x)</tex> og <tex>F(a)-F(b)</tex> er lik arealet mellom <tex>x</tex>-aksen og funksjonen <tex>f(x)</tex> mellom <tex>x=a</tex> og <tex>x=b</tex>.