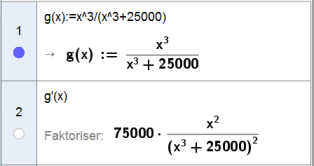S2 2015 vår LØSNING

Diskusjon av denne oppgaven

Sensorveiledning

Vurderingsskjema

Forhandssensurrapport

Oppgave 1

a)

$f'(x) = e^{-2x} \cdot (-2) = -2e^{-2x} $

b)

Brukar brøkregelen med $u=x^2-1$ og $v=x$:

$$g'(x)= \frac{u'\cdot v - u \cdot v'}{v^2} =\frac{2x\cdot x - (x^2-1)\cdot 1}{x^2} = \frac{2x^2-x^2+1}{x^2} = \frac{x^2+1}{x^2} $$

c)

Brukar produktregelen til å derivere $(3x+1)\cdot e^x$:

$h'(x)=3 \cdot e^x + (3x+1) \cdot e^x = (3x+4)e^x $

Oppgave 2

a)

Jeg leser av nullpunktene på grafen:

$x=-3$, $x=-1$ og $x=3$.

Da vet vi at $(x+3)$, $(x+1)$ og $(x-3)$ er faktorer i polynomet $f(x)$.

$f(x)=(x+3)(x+1)(x-3)$

b)

Jeg bruker ett av nullpunktene, f.eks. $x=3$.

Vi vet at $f(x)=0$ for $x=3$:

$f(3)=0 \\ 3^3 +3^2+k\cdot 3 + k =0 \\ 27 +9 +3k +k =0 \\ 4k =-36 \\ k = -9 $

Oppgave 3

a)

En rekke er aritmetisk dersom differansen mellom et ledd og leddet foran er konstant.

$a_n - a_{n-1} = d$

b)

Av figuren ser vi at veggen er slik at 1. rad (fra toppen) består av 1 murstein, 2. rad består av 2 murstein, 3. rad består av 3 murstein osv. Siste raden består av 20 murstein.

Summen av alle mursteinene blir da en aritmetisk rekke:

$1+ 2 + 3 + \cdots + 20 $

Differansen $d$ mellom hvert ledd er 1. $a_1 =1$ og $n=20$.

Vi bruker formelen for summen av en aritmetisk rekke:

$$S_n = \frac{a_1+a_n}{2} \cdot n \\ S_{20} = \frac{1+20}{2} \cdot 20 = 210 $$

Mureren vil trenge 210 murstein til denne veggen.

Oppgave 4

a)

\begin{align*} x&=0,555 \dots \\ &= 0,5 + 0,05 + 0,005 + \dots \\ &= \frac{5}{10} + \frac{5}{100} + \frac{5}{1000} + \dots \\ &= \frac{5}{10} + \frac{5}{10^2} + \frac{5}{10^3} + \dots \end{align*}

Dette er en geometrisk rekke med $k=\frac{1}{10}$ og $a_1 = \frac{5}{10}$.

Siden $-1<k<1$, vil rekken konvergere med summen

$$s=\frac{a_1}{1-k} \\ x= \frac{\frac{5}{10}}{1-\frac{1}{10}} = \frac{\frac{5}{10}}{\frac{9}{10}} = \frac{5}{9} $$

b)

\begin{align*} y &=0,232323 \dots \\ &=0,23 + 0,0023 + 0,000023 + \dots \\ &=\frac{23}{100}+\frac{23}{10000} + \frac{23}{1000000} + \dots \\ &=\frac{23}{10^2}+\frac{23}{10^4} + \frac{23}{10^6} + \dots \end{align*}

Dette er en geometrisk rekke med $k=\frac{1}{100}$ og $a_1=\frac{23}{100}$.

Siden $-1<k<1$, vil rekken konvergere med summen:

$$s=\frac{a_1}{1-k} \\ y= \frac{\frac{23}{100}}{1-\frac{1}{100}} = \frac{\frac{23}{100}}{\frac{99}{100}} =\frac{23}{99} $$

Oppgave 5

a)

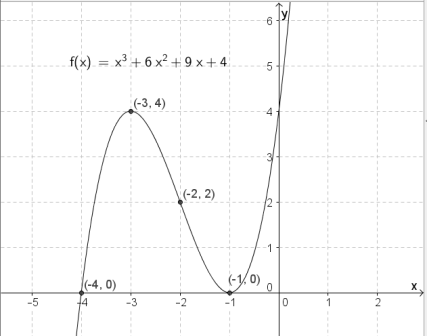
$f(-1) = (-1)^3+6 \cdot (-1)^2 + 9 \cdot (-1) +4 = -1 + 6 - 9 +4 = 0 $

For å finne eventuelle andre nullpunkter kan vi bruke polynomdivisjon til å løse likningen $f(x)=0$.

Siden $f(x)=0$ for $x=-1$, vet vi at divisjonen $f(x):(x+1)$ går opp:

$(x^3+6x^2+9x+4):(x+1)= x^2+5x+4 $

Bruker abc-formelen til å løse likningen $x^2+5x+4=0$:

$$x= \frac{-5\pm \sqrt{5^2-4\cdot 1\cdot 4}}{2} = \frac{-5\pm \sqrt{9}}{2} = \frac{-5\pm3}{2}\\ x=-1 \vee x=-4$$

Nullpunktene til $f$ er $x=-1$ og $x=4$.

b)

Grafen til $f$ har eventuelle topp- eller bunnpunkter der $f'(x)=0$.

$f'(x)=3x^2+12x+9 = 3(x^2+4x+3)$

Løser likningen $x^2+4x+3 =0 $:

$$ x=\frac{-4\pm \sqrt{4^2-4\cdot 1 \cdot 3}}{2\cdot 1} = \frac{-4 \pm \sqrt{16-12}}{2} = \frac{-4\pm 2}{2} \\ x=-3 \vee x=-1 $$

$\Rightarrow f'(x)= 3(x+1)(x+3) $

Bruker det faktoriserte uttrykket til å tegne fortegnslinje for $f'(x)$:

Av fortegnslinja ser vi at $f'(x)$ skifter fortegn fra $+$ til $-$ i $x=-3$, og fra $-$ til $+$ i $x=-1$.

$f(-3)=(-3)^3+6 \cdot (-3)^2 + 9 \cdot (-3) + 4 = -27 + 54 - 27 +4 = 4 \\ f(-1) = 0 $

Grafen til $f$ har et toppunkt i $(-3,4)$ og et bunnpunkt i $(-1, 0)$.

c)

Grafen til $f$ har eventuelle vendepunkter der $f' '(x)=0$.

$f' '(x) = 6x+12 = 6(x+2)$

$6(x+2)=0 \\ x= -2 $

Tegner fortegnslinje for $f' '(x)$:

Vi ser at $f' '(x)$ skifter fortegn når $x=-2$.

$f(-2)= (-2)^3+6 \cdot (-2)^2 + 9 \cdot (-2) +4 = -8 +24 -18 +4 = 2$

Grafen til $f$ har et vendepunkt i $(-2, 2)$.

d)

Oppgave 6

a)

Summen av alle sannsynlighetsverdiene i en sannsynlighetsfordeling skal være lik 1.

Det gir oss første likning: $a+b+c=1$

Forventningsverdien regner vi ut slik: $\mu=E(X)=\sum x_i \cdot P(X=x_i) $ som gir:

$\mu=E(X)= 0 \cdot a + 1 \cdot b + 2 \cdot c = b+2c $

Det gir oss andre likning: $b+2c=\frac{1}{2}$

Variansen regner vi ut slik: $Var(X)= \sum (x_i - \mu)^2 \cdot P(X=x_i) $ som gir:

$ Var(X)= (0-\frac{1}{2})^2 \cdot a + (1-\frac{1}{2})^2 \cdot b + (2-\frac{1}{2})^2 \cdot c = \frac{1}{4}a + \frac{1}{4}b + \frac{9}{4} c $

Det gir oss tredje likning: $ \frac{1}{4}a + \frac{1}{4}b + \frac{9}{4} c = \frac{1}{2} \\ a + b +9c = 2 $

b)

Jeg starter med andre likning: $ b= \frac{1}{2} -2c $

Setter dette inn i første likning: $ a+ \frac{1}{2} -2c +c = 1 \\ a=\frac{1}{2}+c$

Setter inn i siste likning: $(\frac{1}{2}+c)+(\frac{1}{2}-2c)+9c =2 \\ 8c = 1 \\ c= \frac{1}{8} $

$a=\frac{1}{2}+\frac{1}{8}= \frac{5}{8} \\ b= \frac{1}{2}-\frac{2}{8} = \frac{2}{8} = \frac{1}{4} $

Oppgave 7

a)

$x=90$ gir

$z=\frac{x-\mu}{\sigma}= \frac{90-100}{20} = \frac{-10}{20}= -\frac{1}{2} = -0,50 $

Denne $z$-verdien kan vi slå opp i tabellen for standard normalfordeling:

$P(X\leq 90)= P(Z\leq -0,50)=0,3085$.

Sannsynligheten for at en tilfeldig valgt hjortebukk veier mindre enn 90 kg er ca. 31 %.

b)

$x=110$ gir:

$z=\frac{110-100}{20}=\frac{10}{20}=0,50$

$P(90 \leq X \leq 110) = P(-0,50 \leq Z \leq 0,50) \\ = P(Z\leq 0,50) - P(Z\leq -0,50) \\ = 0,6915 - 0,3085 =0,3830 $

Sannsynligheten for at en tilfeldig valgt bukk veier mellom 90 og 110 kg er 38,3 %.

Oppgave 8

Jeg ser først på funksjonen $f$:

Når $x\rightarrow -\infty$ vil $e^{-x} \rightarrow \infty$.

Da vil $\frac{100}{1+e^{-x}} \rightarrow 0$ og $f(x) \rightarrow 0 -25 = -25 $

Den eneste grafen som passer med dette er graf (4).

Nå ser vi på funksjonen $g$:

Når $x \rightarrow \infty $ vil $e^{-(x-5)} \rightarrow 0 $.

Da vil $g(x) \rightarrow \frac{100}{1+0} = 100 $

Den eneste grafen som flater ut ved 100, er graf (1).

Graf (4) hører til $f$, og graf (1) hører til $g$.

Oppgave 1

a)

Jeg legger tabellen inn i regnearket i GeoGebra, høyreklikker og velger "Lag liste med punkt".

Så skriver jeg inn kommandoen "RegPoly[Liste1, 2]" siden oppgaven sier at vi skal finne et andregradsuttrykk.

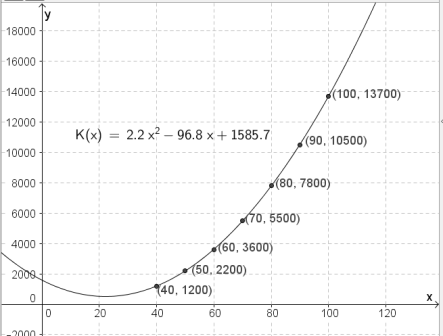
Jeg får denne funksjonen:

$K(x)=2,2x^2 - 96,8x + 1585,7 $

b)

Overskuddet er størst når grenseinntekten er lik grensekostnaden.

Vi må altså finne $p$ slik at

$K'(75)=I'(75)$

Løser dette i CAS:

Overskuddet $O(x)= I(x)-K(x)$.

Dersom overskuddet skal bli størst mulig ved produksjon og salg av 75 enheter, må $p$ være 230.

Da er overskuddet 10669 kroner.

c)

Jeg starter med å skrive om formelen for $x$, slik at jeg får et uttrykk for $p(x)$:

$x=200-1,2p \\ p(x)= \frac{200-x}{1,2} $

Dette uttrykket definerer jeg i GeoGebra, og bruker deretter at $I(x) = p(x) \cdot x $.

Så løser jeg likningen $K'(x)=I'(x)$ for å finne ut hvilken produksjonsmengde som gir størst overskudd.

Til slutt regner jeg ut $p(x)$ for denne produksjonsmengden.

Prisen som vil gi det største overskuddet per dag er 130,50 kroner.

Oppgave 2

a)

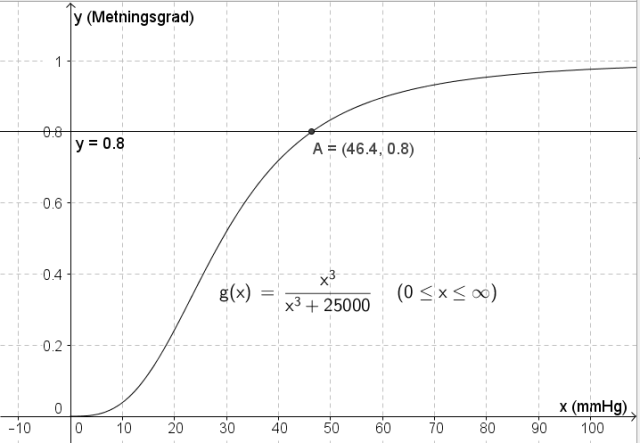
Jeg bruker kommandoen "g(x)=Funksjon[x^3/(x^3+25000), 0, inf]" til å tegne grafen.

b)

Jeg legger inn en horisontal linje for "y=0,8" og bruker "skjæring mellom to objekt" til å finne skjæringspunktet $A=(46.4, 0.8)$ mellom denne linja og grafen til $g$. (Se figur av grafen i oppg. a))

Deltrykket $x$ må være større enn 46,4 mmHg for at metningsgraden $g(x)$ skal være større enn 0,8.

c)

Jeg bruker CAS til å derivere $g(x)$. (Jeg trykker "Faktoriser" for å vise uttrykket på faktorisert form.)

$$g'(x)=\frac{75000x^2}{(x^3+25000)^2}$$

Vi vet at $x^2>0$ for alle $x$

Vi ser at både teller og nevner i $g'(x)$ da blir positive for alle $x$.

Når $g'(x)>0$ stiger grafen til $g(x)$. Metningsgraden øker dersom deltrykket øker.

Oppgave 3

Jeg setter opp følgende hypoteser:

$H_0: \mu=10 \quad$ (Fettinnholdet er 10 g)

$H_1: \mu>10 \quad$ (Fettinnholdet er mer enn 10 g)

Vi har kontrollert 10 hamburgere. Til sammen er fettinholdet (i gram) i disse 10 hamburgerene: $11+10+11+12+9+10+11+12+10+11 = 107 $

Vi går ut fra at $H_0$ gjelder.

Vi lar $X_\Sigma$ være summen av fettinnhold i 10 tilfeldige hamburgere.

I følge sentralgrensesetninga er $X_\Sigma$ da normalfordelt, med

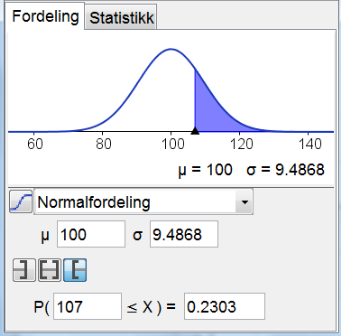
$\mu_{X_\Sigma}= n \cdot \mu = 10 \cdot 10 = 107$ og $\sigma_{X_\Sigma}= \sqrt{n} \cdot \sigma = \sqrt{10} \cdot 3 \approx 9,49 $

Vi skal nå finne p-verdien for testen vår, $P(X_\Sigma \geq 107)$. (Sannsynligheten for at det samla fettinholdet i 10 hamburgere er 107 gram eller mer, forutsatt at $H_0$ gjelder.)

Jeg bruker sannsynlighetskalkulator i GeoGebra:

P-verdien blir $P(X_\Sigma \geq 107)=0,23= 23 \% $

P-verdien er $23 \% > 5 \%$. Vi kan ikke forkaste nullhypotesen. Vi kan ikke konkludere med at fettinnholdet i hamburgerene er for stort, på grunnlag av denne kontrollen.

Oppgave 4

a)

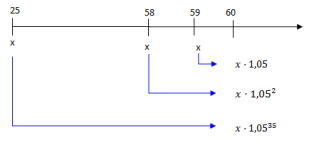
Jeg lager et skjema for å få oversikt. Totalt sparer hun 35 beløp. Jeg regner alt om til sluttverdier.

Summen av alle sluttverdiene skal bli 2 000 000:

$x \cdot 1,05 + c \cdot 1,05^2 + \dots x \cdot 1,05^{35} = 2 000 000$

Dette blir en geometrisk rekke med 35 ledd.

$a_1 = x \cdot 1,05$ og $k=1,05$.

$$S_{35} = x \cdot 1,05 \frac{1,05^{35}-1}{1,05-1} = 2000000 $$

Løser likningen med CAS i GeoGebra:

Vi får $x\approx21000 $ dersom vi runder ned til hele 1000.

b)

Jeg regner her med at hun har 2 millioner på konto den dagen hun fyller 60 år. (Dersom hun har spart 21000 kroner hvert år vil det egentlig være litt mindre på kontoen.)

Dersom Kristin ikke hadde tatt ut 200 000 kroner hvert år, hadde hun den dagen hun fyller 65 år hatt:

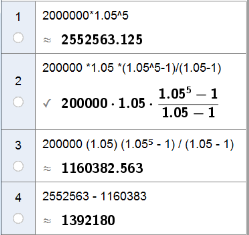
$ 2 000 000 \cdot 1,05^5 = 2 552 563 $ kr på kontoen.

Nå kan vi finne ut hva de 5 uttakene på 200 000 kr hvert år hadde forrentet seg til dersom hun hadde spart de.

Summen av disse sluttverdiene blir:

$200 000 \cdot 1,05 + 200 000 \cdot 1,05^2 + 200 000 \cdot 1,05^3 + 200 000 \cdot 1,05^4 + 200 000 \cdot 1,05^5 $

Dette er en geometriske rekke. $a_1=200 000 \cdot 1,05 $ og $k=1,05$.

Jeg bruker sumformelen og regner ut summen vha. CAS:

Den dagen hun fyller 65 år har Kristin 1 392 180 kroner på kontoen.

Oppgave 5

a)

Når grafen skjærer y-aksen, er $x=0$.

Regner ut $f(0)$:

$$f(0)=\frac{a}{1+b\cdot e^0} = \frac{a}{1+b} $$

b)

I vendepunktet er $f' '(x)=0$.

Jeg bruker CAS i GeoGebra til å løse likningen $f' '(x)=0$. Etterpå settter jeg løsningen inn i uttrykket for $f(x)$.

c)

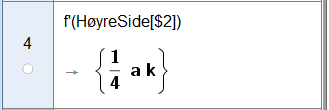
Stigningstallet til tangenten i punktet $V$ er lik den deriverte av $f$ i punktet $V$.

Jeg regner ut $f'(x)$, der jeg setter inn $x$-koordinaten til vendepunktet. (Som vi fant i oppg. b))