S1 2013 vår LØSNING

Oppgave 1

a)

$2lgx + 3 = 5 \\ 2lgx =2 \\ lg x=1 \\ 10^{lgx} 10^1 \\x=10$

b)

$2x^2+2x=12\\ 2x^2+2x-12=0 \\ x= \frac{-2\pm \sqrt{4+4 \cdot 2 \cdot 12}}{4} \\ x= \frac{-2 \pm 10}{4} \\ x= -3 \vee x= 2$

Oppgave 2

<math> \left[ \begin{align*} y=6 - x^2 \\ y +4= -3x \end{align*}\right] </math>

<math> \left[ \begin{align*} y=6 - x^2 \\ 6- x^2 +4= -3x \end{align*}\right] </math>

<math> \left[ \begin{align*} y=6 - x^2 \\ -x^2+3x +10=0 \end{align*}\right] </math>

<math> \left[ \begin{align*} y=6 - x^2 \\ x= \frac{-3 \pm \sqrt{9+ 4 \cdot 1 \cdot 10}}{-2}\end{align*}\right] </math>

<math> \left[ \begin{align*} y=6 - x^2 \\ x= \frac{-3 \pm 7}{-2}\end{align*}\right] </math>

<math> \left[ \begin{align*} y=6 - x^2 \\ x= 5 \vee x = -2\end{align*}\right] </math>

Innsatt i første likning gir det løsningene:

$(-2, 2) \wedge (5, -19)$

Oppgave 3

a)

$ \frac{2^{-3} \cdot a^0 \cdot (a \cdot b)^2}{2^{-4} \cdot a^{-1} \cdot b^2}= \frac{2^4a^3b^2}{2^3b^2} = 2a^3$

b)

$lg(ab) ^2- lg ( \frac{a^3}{b^2}) + lg(ab^2)= \\ 2(lga +lgb) - ( lg a^3 - lg b^2 ) + lga + lg b^2 = \\ 2lga+ 2lgb -3lga + 2lgb +lga + 2lgb = \\ 6 lgb$

Oppgave 4

a)

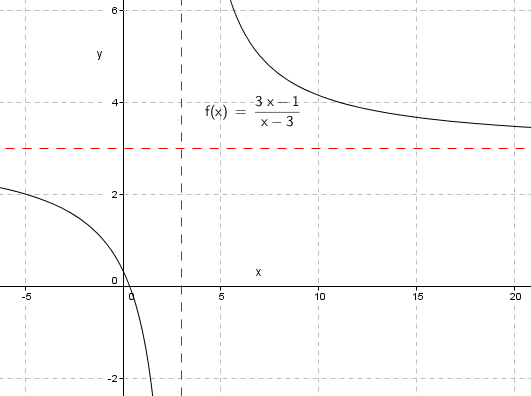
Her er grafen tegnet i Geogebra. Dette er del en, så det kan ikke du gjøre. Gjør slik:

Finn vertikal asymptote, den x verdi som gjør nevner lik null. x - 3 = 0 gir løsning for x = 3. Tegn asymptoten inn i koordinatsystemet.

Finn horrisontal asymptote. Del alle ledd i teller og nevner med x. Da får du: $\frac{3- \frac 1x}{1 - \frac 3x}$ Når absoluttverdien av x blir stor, går verdien av uttrykket mot 3. Tegn den horrisontale asymptoten inn i koordinatsystemet.

Lag en verditabell der du velger seks x verdier, tre mindre enn x = 3, og tre større. For eksempel x lik -5, 0, 2 og 4, 6 og 8. Regn ut funksjonsverdien for disse og plott punktene i koordinatsystemet. Trekk glatte kurver. Skissen av funksjonen bør ligne på den over.

b)

Gjennomsnittlig veksthastighet fra x = 4 til x = 7: $\frac{f(7) - f(4)}{3} = \frac{5-11}{3} =-2$

Den gjennommsnittlige vekstfarten fra x= 4 til x =7 er - 2.

Oppgave 5

a)

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1

b)

Husk at det første tallet står på nullte rad.

$\binom 20 = 1$ (første tall på rad nr. tre, som jo egentlig er rad nr. to, siden første er nullte)

$ \binom31= 3 \\ \binom52= 10 \\ \binom83 = 56 $

c)

$ \frac{\binom 31 \cdot \binom 52 }{ \binom 83} = \frac{2 \cdot 10}{56} = \frac {15}{28}$

Sannsynligheten for å trekke en gutt og to jenter fra en gruppe på åtte er $\frac{15}{28}$.

d)

Ut fra talltrekanten i oppgave a ser man (på linje 9) at det må være to eller seks medlemmer i komiteen.

Oppgave 6

a)

$\frac {2}{3}x^3+x^2-12x+1 \\ f ' (x) = 2x^2+2x-12$

b)

$f ' (x)= 0 \\ 2x^2 + 2x - 12 = 0 \\ x = -3 \vee x=2$

(samme som oppgave 1b)

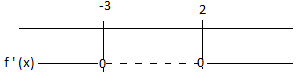
f er strengt voksende: $x \in <\leftarrow] \cup [2, \rightarrow>$

f er strengt avtagende $x \in [-3, 2]$

Oppgave 7

Tog A; kjører med farten v i t timer. $ v = \frac st \Rightarrow vt =s \Rightarrow vt =120$

Tog B: kjører med en gjennomsnittsfart 20 km/ større enn tog A, altså (v + 20), det bruker da en time mindre enn tog A, altså (t-1). Avstanden er den samme: altså blir (v+20)( t - 1) = 120

<math> \left[ \begin{align*} vt = 120 \\ (v+20)(t-1) = 120 \end{align*}\right] </math>

<math> \left[ \begin{align*} v = \frac{120}t \\ (\frac{120}t +20)(t-1) = 120 \end{align*}\right] </math>

<math> \left[ \begin{align*} 120 - \frac{120}{t} +20t-20 = 120 \end{align*}\right] </math>

<math> \left[ \begin{align*} t^2-t-6=0 \end{align*}\right] </math>

t = 3 timer

Det betyr at tog A holder en gjennomsnittsfart på 40 km/t og tog B 20km/t raskere, altså 60 km/t.

Oppgave 1

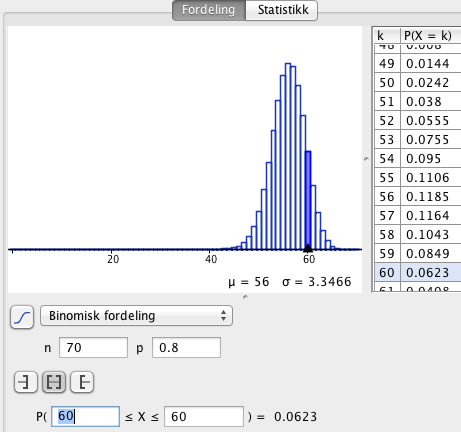
a)

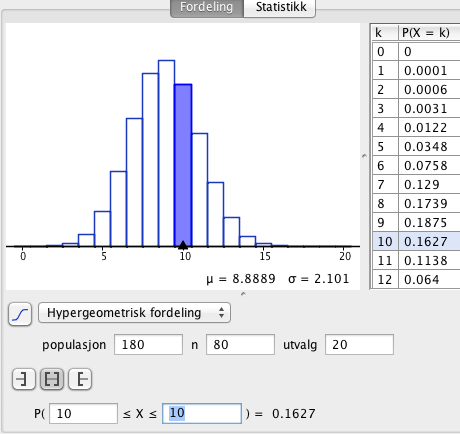
Sannsynligheten for akkurat 60 epler kan selges til vanlig forbruk er 6,2%.

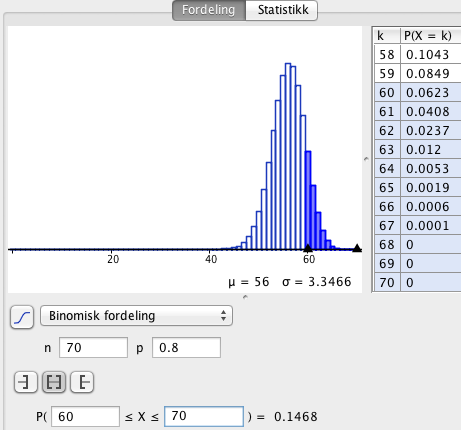
b)

Sannsynligheten for at minst 60 epler kan selges til vanlig forbruk er 14.7%.

c)

Sannsynligheten for 10 epler av type A og 10 epler av type B, er 16,3%.

Oppgave 2

a)

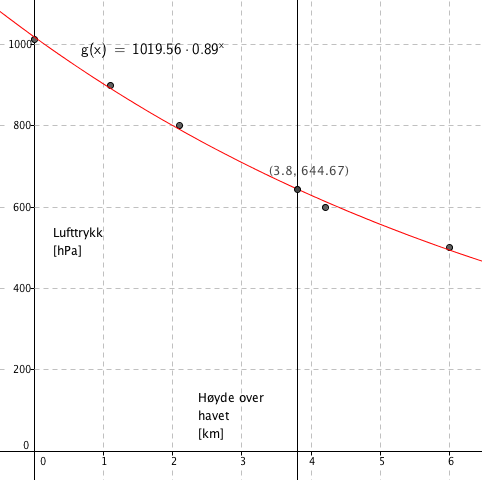
En eksponentiell model som passer med dataene er:

$ p(x) =1019,56 \cdot 0,89^x$

b)

Fra Figuren i a ser man at lufttrykket ved Titicacasjøen vil være ca 645 hPa.

c)

$ p(x) = 700 \\ 1019,56 \cdot 0,89^x = 700 \\ x \cdot lg 0,89 = lg 0,687 \\ x \approx 3,2$

Man befinner seg ca 3,2 km over havnivå, dersom trykket er 700 hPa.

Oppgave 3

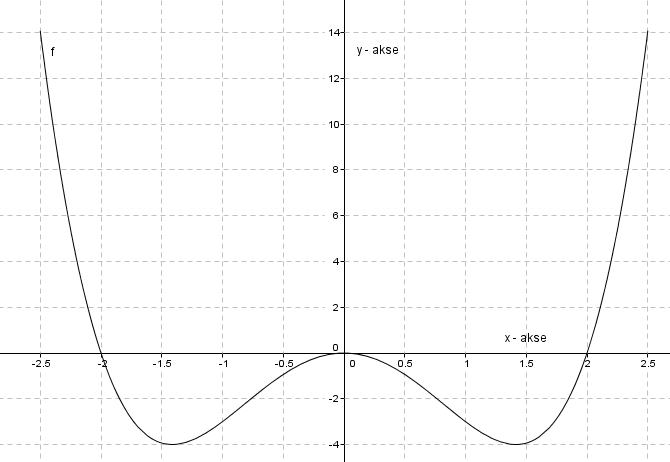
a)

b)

$f(x)= x^4-4x^2\\ f(0)=0$

Altså er skjæring med y-aksen lik null.

$f(x)= 0 \\ x^2(x^2-4) =0 \\ x=0 \vee x^2-4 =0 \\ x=0 \vee x= -2 \vee x=2 $

Nullpunkter: (-2,0), (0, 0) og (2, 0).

c)

$f ' (x)= 4x^3 -8x \\ f' (x)=0 \\ 4x^3 -8x=0 \\ 4x(x^2 -2) = 0 \\ x =0 \vee x = - \sqrt 2 \vee x = \sqrt 2$

Det finnes tre ekstremalpunkter:

$(0, f(0)) = (0,0) \\ (- \sqrt 2, f(-\sqrt 2 )) = (-\sqrt2, -4 )\\ (\sqrt 2, f(\sqrt 2 )) = (\sqrt2, -4 ) $

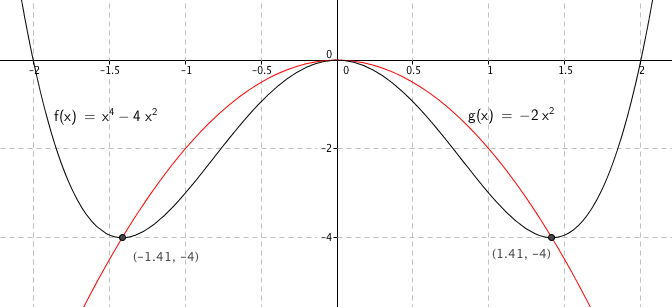
d)

g skal gå gjennom minimumspunktene til f.

$g(x)= ax^2 \\ -4 =a (\pm \sqrt 2)^2 \\ a= -2$

e)

Oppgave 4

a)

x = tonn Godlaks

y = tonn Gladlaks.

Man kan maksimum produsere 35 tonn per uke:

$x + y \leq 35$

Det minste man kan produsere av foret er ingenting:

$x \geq 0 \wedge y \geq 0$

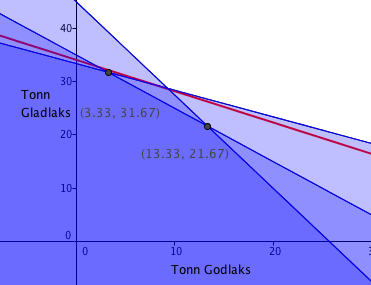
Begrennsninger stoff A (i tonn): $0,3x + 0,6y \leq18$

Begrennsninger stoff B (i tonn): $0,7x + 0,4 y \leq 20$

( Området er avgrenset av aksene, det kommer ikke fram på figuren.)

b)

For at inntektene skal bli størst mulig må det produseres 3,33 tonn av Godlaks og 31,67 tonn av Gladlaks, se rød nivålinje i oppgave a.

I(x,y) = 5000x + 8500y.

I (3,33 , 31,67) = 285 845 kroner.

Inntektene bli 285845 kroner, når det produserer 3,33 tonn Godlaks og 31,67 tonn Gladlaks.

Oppgave 5

a)

Kostnadsfunksjon : $f(x) = 55 + 0,01x^2$

Skal ikke overstige 200:

$g(x)= 200 \\ 55 + 0,01x^2 = 200 \\ x= 120$

Det kan maksimalt produseres 120 enheter, dersom kostnadene ikke skal overstige 200.

b)

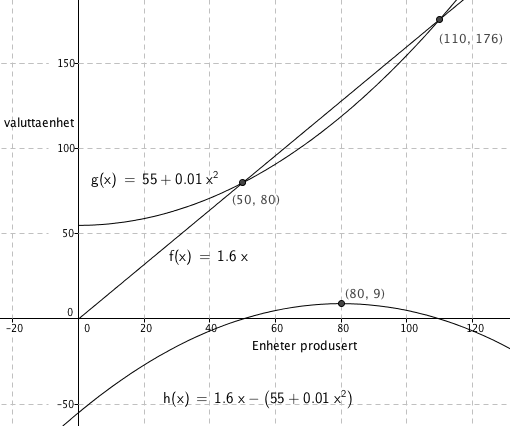
f = inntekt

g = kostnad

h = overskudd.

Fra Figuren ser man at det er overskudd når det produseres mere enn 50 og mindre enn 110 enheter. Overskuddet er størst når det produseres 80 enheter. Da er overskuddet 9.

c)

Dersom det ikke selges noen enheter, er intektene null. Inntektsfunksjonen starter derfor i origo. Dersom aktiviteten skal ballansere må kostnader og intekter være like store, det betyr at inntektsfunksjonen må tangere kostnadsfunksjonen i et punkt. Enhetens pris, p, er stigningstallet til tangenten til kostnadsfunksjonen, og tangenten er altså sammenfallende med grafen til intektsfunksjonen.

d)

$p < f' (a)$ gir kostnader høyere enn intekter for alle x.

$p> f'(a)$ gir skjæring mellom f og g, altså overskudd i et inteval for x.

$p = f'(a)$ gir tangering mellom f og g, altså balanse.

$f'(x) = 0,02x \\ f'(a) = p \approx1,47 \\ 0,02a = 1,47 \\ a \approx 74 $

Man må produsere 74 enheter for å være i balanse.