1T 2014 vår LØSNING

Oppgaven som pdf

Tråd om denne oppgaven på Matteprat

Enda en tråd om denne oppgaven på Matteprat

Løsning laget av Nebu

Oppgave 1:

$2,5 \cdot 10^{15} \cdot 3,0 \cdot 10^{-5} = 7,5 \cdot 10^{15+(-5)} = 7,5 \cdot 10^{10}$

Oppgave 2:

$9^{ \frac12}\cdot 6^0 \cdot 4^{-1} \cdot \sqrt[3]{8^2} = \\ (3^2)^{\frac12} \cdot 1 \cdot \frac 14 \cdot \sqrt[3]{2^6} = \\ \frac34 \cdot 2^2 = 3$

Oppgave 3:

$2^{2-x} \cdot 2^{1+2x} =32 \\ 2^{2-x+1+2x} = 2^5 \\ 3+x=5 \\ x=2$

Oppgave 4:

$x^2 +8x +c \\$ Vi har at $a^2 +2ab +b^2 = (a+b)^2$

Dvs: c = $4^2 = 16$

Oppgave 5:

$[2x-3y=-7 \\ 3x-y=7 ] \\ [ y=3x-7 \\ 2x -3(3x-7) = -7] \\ 2x-9x + 21 = -7 \\ - 7x = - 28 \\ x= 4 \\ 3x-y=7 \\ 12 - y =7 y=5 \\ x = 4 \wedge y = 5$

Oppgave 6:

$\frac {6}{x-3} - \frac {5x+15}{x^2-9}+ 1= \\ \frac{6}{x-3} - \frac {5(x+3)}{(x+3)(x-3)}+ \frac {x-3}{x-3} = \\ \frac {6-5+ x - 3 }{x-3}= \\ \frac {x-2}{x-3}$

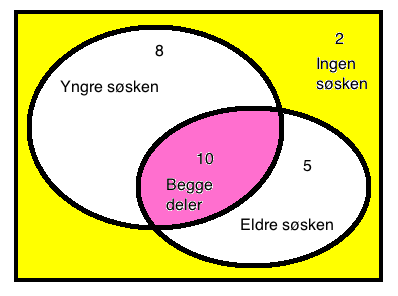
Oppgave 7:

a)

b)

P(eldre men ikke yngre søsken) = $ \frac {5}{25} = \frac 15$

c)

P(yngre søsken gitt eldere søsken) = $\frac {10}{15}= \frac{2}{3}$

Oppgave 9:

$f(x)= x^2+2x-3$

a)

Nullpunkt: $f(x)=0 \\ x^2+2x-3 = 0 \\ x= \frac{-2 \pm \sqrt{4-4 \cdot (-3)}}{2} \\ x= \frac{-2 \pm 4}{2} \\x= -3 \vee x= 1$

Nullpunktene er (-3, 0 ) og (1, 0).

b)

$f´(x) = 2x+2 \\f´(x)=2 \Rightarrow x = 0 $

Tangeringspunkt. ( 0 , f(0) ) som er (0, -3)

Likning for tangenten:

$y = ax+b \\ -3 = 2 \cdot 0 -3 \\ b = -3 \\ y=2x-3$

Den siste utregningen kunne vi sløyfet i dette tilfellet, siden vi vet at tangeringen skjer på y aksen (x = 0).

Oppgave 10:

$f(x) = x^2+bx+c $

Grafen skjærer y - aksen i (0, 4), dvs. f(0) = 4, altså er c = 4.

Funksjonen f har ett nullpunkt, dvs: $ b^2 - 4ac = 0 \\ b= \pm 4 \\ f(x)= x^2-4x+ 4 \vee f(x)= x^2+ 4x+ 4 $