1P 2014 vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| Linje 13: | Linje 13: | ||
==Oppgave 3== | ==Oppgave 3== | ||
a) | a) | ||
$\frac{(x+4) \cdot 3}{2}=9 \\ | $\frac{(x+4) \cdot 3}{2}=9\\ | ||
\frac{3x+12}{2}=9 \\ | \frac{3x+12}{2}=9\\ | ||
3x+12=18 \\ | 3x+12=18\\ | ||
3x=6 \\ | 3x=6 \\ | ||
x=2$ | x=2$ | ||
b) $\frac{(x+4cm) \cdot 3cm}{2}=9cm^2$ | b) $\frac{(x+4cm) \cdot 3cm}{2}=9cm^2$ | ||
Sideversjonen fra 25. mai 2014 kl. 09:15
Del 1
Oppgave 1
$6mm \cdot 50 = 300mm = 30cm$
Feilen vil bli 30cm i virkeligheten.
Oppgave 2
$\frac{617L}{15,3L} \approx \frac{615L}{15L} = 41$
Du trenger omtrent 41 kanner.
Oppgave 3
a) $\frac{(x+4) \cdot 3}{2}=9\\ \frac{3x+12}{2}=9\\ 3x+12=18\\ 3x=6 \\ x=2$
b) $\frac{(x+4cm) \cdot 3cm}{2}=9cm^2$
Ligningen er den samme som i oppgave a, derfor er lengden av den andre parallelle siden lik 2cm.
Oppgave 4
$7 200 000 000 \cdot 0.10 = 720 000 000 $
Halvparten av $720 000 000 = 360 000 000 \\ 720 000 000 + 360 000 000 = 1 080 000 000$
Cirka 1,08 milliarder mennesker har ikke tilgang til rent vann.
Alternativ utregning:
$7,2 \cdot 10^9 \cdot 1,5 \cdot 10^-1 = 10,8 \cdot 10^8 = 1,08 \cdot 10^9$
Oppgave 5
$\frac{100}{500000kr}= \frac{x}{600000kr} \\ x = \frac{100 \cdot 600000kr}{500000kr}=120$
KPI var 120 dette året.
Oppgave 6
Liter saft totalt: $0,2L \cdot 500=100L$
Ren saft: $\frac{1}{10} \cdot 100L = 10L$
Det går 10L ren saft med i 100L ferdigblandet saft.
Oppgave 7
a) $ \sqrt{(2,5m)^2 - (1,5m)^2}=\sqrt{6,25m^2 - 2.25m^2}=\sqrt{4m^2}=2m$
b) $A=5m \cdot 2m = 10m^2$ $V_{jord}=$10m^2 * 0,1m = 1m^3 = 1000L$
Antall sekker: $\frac{1000L}{35L} = 28,571$
Du trenger 29 sekker.
Alternativ utregning:
$30\cdot35L = 1050L$
Man kan bare trekke fra 35L én gang uten at det går under 1000L. Du trenger derfor 29 sekker.
Oppgave 8
a)
Januar: $8 \cdot 20kr + 160kr = 320kr$
Februar: $14 \cdot 20kr + 160kr = 440kr$
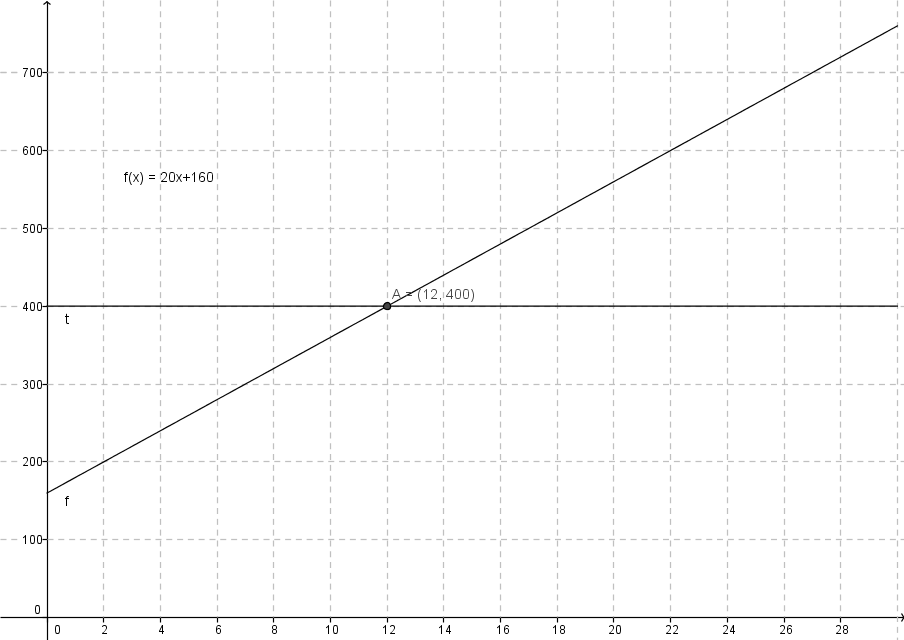
b)
c) Lagde en ny funksjon hvor y = 400 i GeoGebra, brukte skjæringsverktøyet og så at grafene skjærte ved x = 12. Hun må altså trene 12 ganger for at avtalene skal være like billig. Derfor må hun trene 13 ganger eller mer for at avtale 2 skal lønne seg.
d)
Avtale 1: produktet av P og A blir større jo flere ganger hun trener. P og A er derfor ikke omvendt proporsjonale størrelser. P delt på A er det samme som stigningstallet til grafen, altså 20, som er proporsjonalitetskonstanten. P og A er proporsjonale størrelser i avtale 1. Avtale 2: Det koster det ingenting for Kari å trene, og derfor er ikke P og A hverken omvendt proporsjonale eller proporsjonale størrelser.