R2 2013 høst LØSNING

Oppgaven som pdf

Matteprat: Diskusjon omkring denne oppgaven

DEL EN

Oppgave 1

a) $ \displaystyle f(x) = 5x\cos x$

Produktregelen for derivasjon gir at

$ \displaystyle f'(x) = 5\cos x + 5x(- \sin x) = 5\cos x - 5x\sin x = 5(\cos x - x\sin x)$

b) $ \displaystyle g(x) = \frac{\sin (2x)}{x}$

Brøkregelen for derivasjon gir at

$ \displaystyle g'(x) = \frac{2\cos (2x) \cdot x - \sin (2x) \cdot 1}{x^2} = \frac{2x \cos (2x) - \sin (2x)}{x^2}$

Oppgave 2

a) $ \displaystyle \int_0^{1} 2e^{2x} \, \mathrm{d}x = 2 \int_0^{1} e^{2x} \, \mathrm{d}x = 2 \left[ \frac{1}{2}e^{2x} \right]_0^{1} = \frac{2}{2} \left[e^{2x} \right]_0^{1} = e^{2 \cdot 1} - e^{2 \cdot 0} = e^2 - e^0 = e^2 - 1$

b) $ \displaystyle \int 2x \cdot e^x \, \mathrm{d}x$

La $\displaystyle u = 2x$ og $\displaystyle v' = e^x$

Delvis integrasjon gir at

$\displaystyle \begin{align*} \int 2x \cdot e^x \, \mathrm{d}x & = 2x \cdot e^x - \int 2e^x \, \mathrm{d}x + C \\ & = 2xe^x - 2\int e^x \, \mathrm{d}x + C \\ & = 2xe^x - 2e^x + C \\ & = 2e^x(x - 1) + C\end{align*}$

Oppgave 3

a) $\vec{AB} = \left[-2,3,0\right]$ og $\vec{AC} = \left[-2,0,4\right]$

Da blir $\vec{AB} \cdot \vec{AC} = (-2) \cdot (-2) + 3 \cdot 0 + 0 \cdot 4 = 4$

og $\vec{AB} \times \vec{AC} = \left[3\cdot4 - 0\cdot0,-\left((-2)\cdot4 - 0\cdot(-2)\right),(-2)\cdot0 - 3\cdot(-2)\right] = \left[12,8,6\right]$

b)

$\displaystyle \begin{align*} V & = |\frac{1}{6}(\vec{AB} \times {AC})\cdot\vec{AO}| \\ \displaystyle & = |\frac{1}{6}\left[12,8,6\right]\cdot\left[-2,0,0\right]| \\ \displaystyle & = |\frac{1}{6}\left(12(-2) + 8\cdot 0+ 6\cdot0\right)| \\ \displaystyle & = |\frac{1}{6}(-24) \\ \displaystyle & = |- \frac{24}{6}| \\ \displaystyle & = |-4| \\ \displaystyle & = 4\end{align*}$

Eventuelt kan man regne ut volumet ved hjelp av formelen for volum av pyramide, $V = \frac{G\cdot h}{3}$,

hvor $ \displaystyle G = \frac{|\vec{OA}|\cdot|\vec{OB|}}{2} = \frac{2\cdot3}{2} = 3$ og $ \displaystyle h = |\vec{OC}| = 4$.

Da får man $ \displaystyle V = \frac{3\cdot4}{3} = 4$

c) Om man bruker punktet $A(2,0,0)$ og normalvektoren $\vec{AB} \times \vec{AC} = \left[12,8,6\right]$ blir likningen for planet $\alpha$:

$ \displaystyle\begin{align*} 12(x - 2) + 8(y - 0) + 6(z - 0) & = 0 \\ \displaystyle 12x - 24 + 8y + 6z & = 0 \\ \displaystyle 12x + 8y + 6z & = 24 \\ \displaystyle \frac{12x}{24} + \frac{8y}{24} + \frac{6z}{24} & = \frac{24}{24} \\ \displaystyle \frac{x}{2} + \frac{y}{3} + \frac{z}{4} & = 1\end{align*}$

Hvilket skulle vises.

Oppgave 4

a) Rekken er geometrisk fordi neste ledd i rekken genereres ved å multiplisere det forrige leddet med en fast kvotient $\displaystyle k = e^{-1} = \frac{1}{e}$. Ettersom $\displaystyle \frac{1}{e} < 1$, er altså $\displaystyle |k|<1$, hvilket gjør rekken konvergent.

$ \displaystyle S = \frac{a_1}{1-k} = \frac{1}{1-\frac{1}{e}} = \frac{1}{\frac{e}{e} - \frac{1}{e}} = \frac{1}{\frac{e-1}{e}} =\frac{e}{e-1}$

b) I dette tilfellet er $\displaystyle k = e^{-x}$, og rekken er konvergent dersom $\displaystyle |k|<1$.

$ \displaystyle |e^{-x}|<1$

Ettersom $\displaystyle e^{-x}$ alltid vil være positivt, kan man skrive om likningen til

$ \displaystyle \begin{align*} e^{-x} & < 1 \\ \displaystyle \ln(e^{-x}) & < \ln1 \\ \displaystyle (-x)\cdot\ln(e) & < 0 \\ \displaystyle -x & < 0 \\ \displaystyle x & > 0 \end{align*}$

$ \displaystyle S = \frac{a_0}{1-k} = \frac{1}{1-e^{-x}} =\frac{1}{1-\frac{1}{e^x}} = \frac{1}{\frac{e^x}{e^x} - \frac{1}{e^x}} = \frac{1}{\frac{e^{x}-1}{e^{x}}} = \frac{e^x}{e^x - 1}$

Oppgave 5

$\displaystyle N'(t) = 4t + 3$ og $\displaystyle N(0) = 800$

$\displaystyle N(t) = \int (4t + 3)\, \mathrm{d}x = 2t^2 + 3t + C \\$

$\displaystyle \begin{align*} N(0) & = 800 \\ \displaystyle 2\cdot0^2 + 3\cdot0 + C & = 800 \\ \displaystyle 0 + 0 + C & = 800 \\ \displaystyle C & = 800 \end{align*}$ $\displaystyle C = 800 \Rightarrow N(t) = 2t^2+3t + 800\\$

$\displaystyle N(10) = 2\cdot10^2 + 3\cdot10 + 800 = 200 + 30 + 800 = 1030$

Det var altså 1030 individer i populasjonen etter 10 timer.

Oppgave 6

$ \displaystyle f(x) = \frac{1}{2}x^4 - 2x^3 + \frac{5}{2}x$

a) $\displaystyle f'(x) = 2x^3 - 6x^2 + \frac{5}{2}$

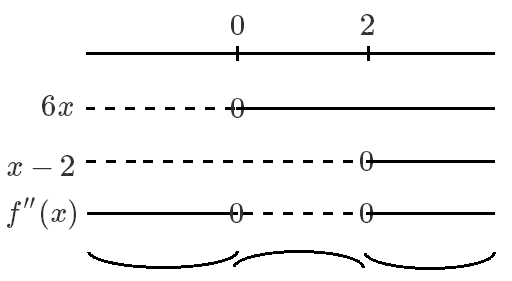
$\displaystyle f ' ' (x) = 6x^2 - 12x = 6x\left(x - 2\right)$

Vendepunkter:

$\displaystyle Vp_1: \left(0,f(0)\right) = \left(0,\frac{1}{2}\cdot0^4 - 2\cdot0^3 + \frac{5}{2}\cdot0\right) = \left(0,0\right)$

$\displaystyle Vp_2: \left(2,f(2)\right) = \left(2,\frac{1}{2}\cdot2^4 - 2\cdot2^3 + \frac{5}{2}\cdot2\right) = \left(2,-3\right)$

b) $\displaystyle Vt_1 - 0 = f ' (0)\cdot(x - 0) \Rightarrow Vt_1 = \left(2\cdot0^3 - 6\cdot0^2 + \frac{5}{2}\right)x \Rightarrow Vt_1 = \frac{5}{2}x$

$\displaystyle Vt_2 - \left(-3\right) = f ' (2)\cdot(x - 2) \\ \displaystyle \Rightarrow Vt_2 + 3 = \left(2\cdot2^3 - 6\cdot2^2 + \frac{5}{2}\right)\left(x - 2\right) \\ \displaystyle \Rightarrow Vt_2 + 3 = -\frac{11}{2}\left(x - 2\right) \\ \displaystyle \Rightarrow Vt_2 + 3 = -\frac{11}{2}x + 11 \\ \displaystyle \Rightarrow Vt_2 = -\frac{11}{2}x + 8$

Oppgave 7

La $\displaystyle V(n) = \frac{1}{1\cdot2} + \frac{1}{2\cdot3} + \frac{1}{3\cdot4} + . . . + \frac{1}{n\cdot(n + 1)}$ og $\displaystyle H(n) = \frac{n}{n+1}$

$\displaystyle V(1) = \frac{1}{1\cdot2} = \frac{1}{2}$ og $\displaystyle H(1) = \frac{1}{1+1} = \frac{1}{2}$

$\displaystyle V(1) = H(1) \Rightarrow$ Påstanden er bevist for $\displaystyle n = 1$

$\displaystyle V(k+1) = \frac{1}{1\cdot2} + \frac{1}{2\cdot3} + \frac{1}{3\cdot4} + . . . + \frac{1}{k\cdot(k + 1)} + \frac{1}{\left(k+1\right)\left(k + 2\right)} \\ \displaystyle = H(k) + \frac{1}{\left(k + 1\right)\left(k + 2\right)} \\ \displaystyle = \frac{k}{k + 1} + \frac{1}{\left(k + 1\right) \left(k + 2\right)} \\ \displaystyle = \frac{k(k + 2) + 1}{\left(k + 1\right) \left(k + 2\right)} \\ \displaystyle = \frac{k^2 + 2k + 1}{\left(k + 1\right) \left(k + 2\right)} \\ \displaystyle = \frac{\left(k+1\right)^2}{\left(k + 1\right)\left(k + 2\right)} \\ \displaystyle = \frac{k+1}{k+2}$

og

$\displaystyle H(k+1) = \frac{k+1}{(k+1)+1} = \frac{k+1}{k+2}$

$\displaystyle V(k+1) = H(k+1) \Rightarrow$ Påstanden er bevist for alle naturlige tall $\displaystyle n$.

Hvilket skulle bevises.

DEL TO

Oppgave 1

a) $\displaystyle F(v) = \frac{2 + 2\cos v}{2}\cdot\sin v = \frac{2\left(1 + \cos v\right)}{2}\cdot\sin v = \left(1 + \cos v\right)\sin v$

Hvilket skulle vises.

Om $\displaystyle v≥\frac{π}{2}$ mister trapeset sin øverste side, og blir derfor til en trekant.

Om $\displaystyle v≤0$ er vinkelen negativ, og trapeset vil ikke lenger være innskrevet i halvsirkelen.

$ \displaystyle v \in <0,\frac{π}{2}>$

b) $\displaystyle F(v) = \left(1+\cos v\right)\sin v $

Produktregelen for derivasjon gir at

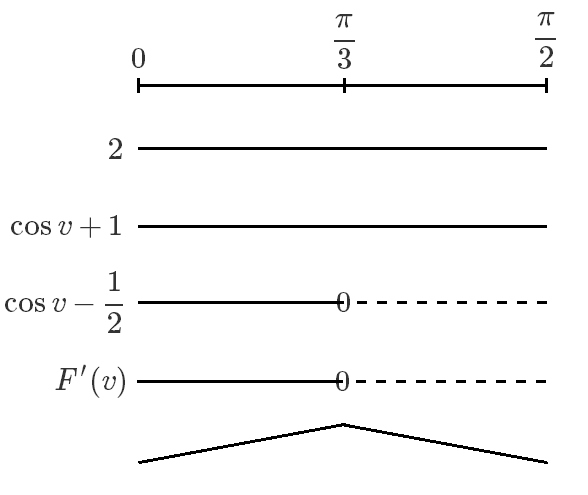
$\displaystyle \begin{align*} F'(v) & = \left(-\sin v\right)\sin v + \left(1 + \cos v\right)\cos v \\ & = \cos^2 v + \cos v - \sin^2 v \\ & = \cos^2 v + \cos v - \left(1-\cos^2 v\right) \\ & = 2\cos^2 v +\cos v - 1 \end{align*}$

$\displaystyle \cos v = \frac{-1± \sqrt{1^2-4\cdot2\left(-1\right)}}{2\cdot2} = \frac{-1 ± 3}{4}$

$\displaystyle \cos v_1 = \frac{1}{2}$ og $\displaystyle \cos v_2 = -1$

$\displaystyle \Rightarrow F'(v) = 2\left(\cos v - \frac{1}{2}\right)\left(\cos v + 1\right)$

$\displaystyle v=\frac{\pi}{3}$ og $\displaystyle F_{maks}(v) = F\left(\frac{\pi}{3}\right) = \left(1+\cos \frac{\pi}{3}\right)\sin \frac{\pi}{3} = \left(1+\frac{1}{2}\right)\frac{\sqrt{3}}{2} = \frac{3}{2}\cdot\frac{\sqrt{3}}{2} = \frac{3\sqrt{3}}{4}$

Oppgave 2

a)

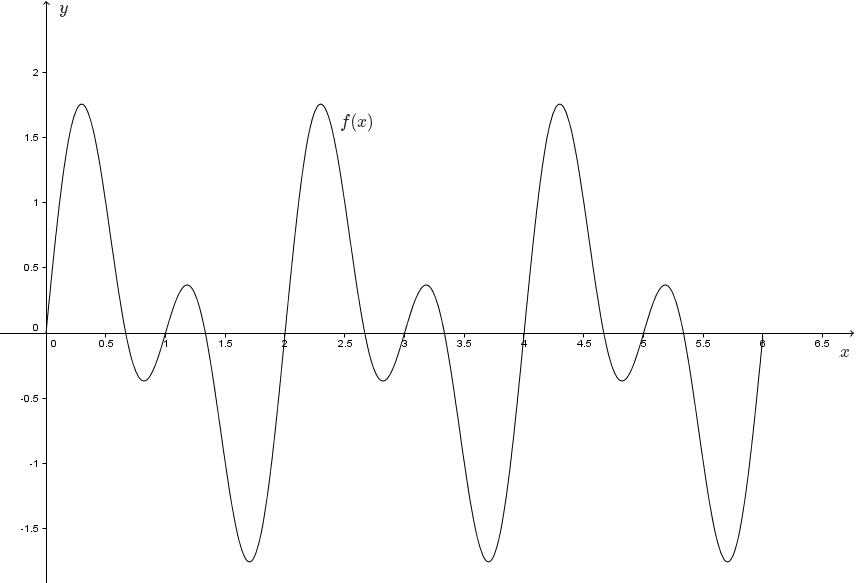
b) Fra tegningen kan man se at grafens utseende i intervallet $\displaystyle x\in\left[0,2\right]$ gjentar seg i intervallet $\displaystyle x \in\left[2,4\right]$ og $\displaystyle\left[4,6\right]$. Altså er det et intervall som gjentas langs $x$-aksen, hvilket betyr at grafen er periodisk.

$\displaystyle p = 2$

c)

$\displaystyle \begin{align*} f(x) & = \sin \left(πx\right) + \sin \left(2πx\right) \\ & = \sin \left(πx\right) + \sin\left(πx + πx\right) \\ & = \sin\left(πx\right) + \left(\sin \left(πx\right)\cos \left(πx\right) + \cos \left(πx\right)\sin \left(πx\right)\right) \\ & = \sin\left(πx\right) + 2\sin \left(πx\right)\cos \left(πx\right) \\ & = \sin\left(πx\right) \left( 1 + 2\cos (πx) \right) \end{align*}$

Hvilket skulle vises.

d)

$\displaystyle\begin{align*} f(x) & = 0 \\ \sin\left(πx\right) \left( 1 + 2\cos (πx) \right) & = 0 \\ \sin\left(πx\right) & = 0 \vee \displaystyle 1 + 2\cos (πx)= 0 \\ πx & =0 + πn \vee \cos\left(πx\right) = -\frac{1}{2} \\ x & = n \vee πx = \frac{2π}{3}+2πn \vee πx = 2 - \frac{2π}{3}+2n \\ x & = n \vee x = \frac{2}{3}+2n \vee x=\frac{4}{3}+2n \end{align*}$

$\displaystyle x\in\left[0,2\right] \Rightarrow \begin{align*} x_1 & = 0 \\ x_2 & = \frac{2}{3} \\ x_3 & = 1 \\ x_4 & = \frac{4}{3} \\ x_5 & = 2\end{align*}$

Nullpunkter: $\displaystyle \left(0,0\right)$, $\displaystyle \left(\frac{2}{3},0\right)$, $\displaystyle \left(1,0\right)$, $\displaystyle \left(\frac{4}{3},0\right)$ og $\displaystyle \left(2,0\right)$

Oppgave 3

a) For enkelhetens skyld kan det være lurt å skrive om likningen $\displaystyle K'(t) = 0,08\cdot K(t)+20\, \mathrm{0}00$ som $\displaystyle y' = 0,08\cdot y + 20\, \mathrm{0}00$

METODE 1

Differensiallikningen kan løses med en integrerende faktor.

$\displaystyle \begin{align*} y' & = 0,08 \cdot y + 20\, \mathrm{0}00 \\ y' - 0,08 \cdot y & = 20\, \mathrm{0}00\, \mathrm{|} \cdot e^{-0,08t} \\ y' \cdot e^{-0,08t} - 0,08 \cdot y \cdot e^{-0,08t} & = 20\, \mathrm{0}00 \cdot e^{-0,08t} \\ \left( y\cdot e^{-0,08t}\right) ' & = 20\, \mathrm{0}00 e^{-0,08t} \\ y\cdot e^{-0,08t} & = \int{20\, \mathrm{0}00e^{-0,08t}}\, \mathrm{d}t \\ y\cdot e^{-0,08t} & = 20\, \mathrm{0}00 \int{e^{-0,08t}}\, \mathrm{d}t \\ y\cdot e^{-0,08t} & = 20\, \mathrm{0}00\cdot \left(-\frac{1}{0,08}\right) \cdot e^{-0,08t} + C \\ y\cdot e^{-0,08t} & = -250\, \mathrm{0}00e^{-0,08t} + C\, \mathrm{|} \cdot\frac{1}{e^{-0,08t}} \\ y & = -250\, \mathrm{0}00 + \frac{C}{e^{-0,08t}} \\ y & = Ce^{0,08t} - 250\, \mathrm{0}00 \\ \Rightarrow K(t) & = Ce^{0,08t} -250\, \mathrm{0}00 \end{align*}$

METODE 2

Differensiallikningen er separabel.

$\displaystyle \begin{align*} y' & = 0,08 \cdot y + 20\, \mathrm{0}00 \\ y' & = 0,08\left( y + 250\, \mathrm{0}00\right)\, \mathrm{|} \cdot\frac{1}{y+250\, \mathrm{0}00} \\ y' \cdot\frac{1}{y+250\, \mathrm{0}00} & = 0,08 \\ \frac{dy}{dt}\cdot\frac{1}{y+250\, \mathrm{0}00} & = 0,08 \\ \frac{1}{y+250\, \mathrm{0}00}\, \mathrm{d}y & = 0,08\, \mathrm{d}t \\ \int{\frac{1}{y+250\, \mathrm{0}00}}\, \mathrm{d}y & = \int{0,08}\, \mathrm{d}t \\ \ln|y+250\, \mathrm{0}00| + C_1 & = 0,08t + C_2 \\ C_2 - C_1 = C_3 \Rightarrow \ln|y+250\, \mathrm{0}00| & = 0,08t + C_3 \\ y+250\, \mathrm{0}00 & = e^{0,08t+C_3} \\ y+250\, \mathrm{0}00 & = e^{C_3}\cdot e^{0,08t} \\ e^{C_3} & = C \Rightarrow y + 250\, \mathrm{0}00 = C e^{0,08t} \\ y & = Ce^{0,08t} - 250\, \mathrm{0}00 \\ \Rightarrow K(t) & = Ce^{0,08t} - 250\, \mathrm{0}00 \end{align*}$

$\displaystyle\begin{align*} K(0) = 20\, \mathrm{0}00 & \Rightarrow 20\, \mathrm{0}00 = Ce^{0,08\cdot 0} - 250\, \mathrm{0}00 \\ & \Rightarrow 20\, \mathrm{0}00 = C - 250\, \mathrm{0}00 \\ & \Rightarrow C = 270\, \mathrm{0}00 \\ & \Rightarrow K(t) = 270\, \mathrm{0}00 e^{0,08t} - 250\, \mathrm{0}00\end{align*}$

b) $\displaystyle K(20) = 270\, \mathrm{0}00 e^{0,08\cdot 20} - 250\, \mathrm{0}00 = 270\, \mathrm{0}00\cdot 4,95 - 250\, \mathrm{0}00 = 1\, \mathrm{0}86\, \mathrm{5}00$

Størrelsen på kapitalen etter $\displaystyle 20$ år blir $\displaystyle 1\, \mathrm{0}86\, \mathrm{5}00$ kroner.

c) $\displaystyle\begin{align*} K(t) & = 270\, \mathrm{0}00 e^{0,08t} - 250\, \mathrm{0}00 \\ K'(t) & = 21\, \mathrm{6}00 e^{0,08t} \\ K'(t) & = 35\, \mathrm{0}00 \\ 21\, \mathrm{6}00 e^{0,08t} & = 35\, \mathrm{0}00 \\ e^{0,08t} & = \frac{35\, \mathrm{0}00}{21\, \mathrm{6}00} \\ 0,08t & = \ln\left(\frac{175}{108}\right) \\ t & = \frac{0,48}{0,08} \\ t & = 6 \end{align*}$

Ifølge modellen vil det ta $\displaystyle 6$ år før kapitalen vokser med $\displaystyle 35\, \mathrm{0}00$ kroner hvert år.

Oppgave 4

a) På høyre side av likningen er den generelle regelen for integrasjon av polynomer brukt:

$\displaystyle\int{x^{a}}\, \mathrm{d}x = \frac{1}{a+1}x^{a+1} + C$

For ordens skyld kan summen av alle integrasjonskonstantene $\displaystyle C_1 + C_2 + C_3 + C_4 + ...$ fra venstre side av likningen bli kalt $\displaystyle C_n$

På høyre side er substitusjon brukt for å integrere.

$\displaystyle\int{\frac{1}{1-x}}\, \mathrm{d}x$

$\displaystyle u = 1-x \Rightarrow du = -dx \Rightarrow \int{\frac{1}{1-x}}\, \mathrm{d}x = -\int{\frac{1}{u}}\, \mathrm{d}u = -\ln|u| + C_m$

På grunn av definisjonsmengden kan absoluttverditegnet elimineres.

$\displaystyle \Rightarrow C_n + x + \frac{1}{2}x^2 + \frac{1}{3}x^3 + \frac{1}{4}x^4 = -\ln\left(1-x\right) + C_m$

$\displaystyle C_m - C_n \Rightarrow x + \frac{1}{2}x^2 + \frac{1}{3}x^3 + \frac{1}{4}x^4 + . . . = -\ln\left(1-x\right) + C$

Hvilket skulle vises.

En kan se at den uendelige rekken på venstre side av likningen er formulert slik at graden til $\displaystyle x$ øker for hvert ledd. Derfor vil aldri leddet $\displaystyle a\cdot x^0$ (hvor $\displaystyle a$ er en konstant) dukke opp, hvilket betyr at det ikke eksisterer noe konstantledd på venstre side av likningen. Det er derfor unødvendig å skrive det på høyre side av likningen, hvilket betyr at $\displaystyle C = 0$.

b) $\displaystyle x=\frac{1}{2} \Rightarrow \frac{1}{1}\cdot\frac{1}{2^1} + \frac{1}{2}\cdot\frac{1}{2^2} + \frac{1}{3}\cdot\frac{1}{2^3} + \frac{1}{4}\cdot\frac{1}{2^4} + ... = -\ln\left(1-\frac{1}{2}\right) = \ln\left(\frac{1}{2}\right)^{-1} = \ln2$

Hvilket skulle vises.