R1 2013 vår LØSNING

Eksamensoppgaven som pdf

Diskusjon av denne oppgaven

Løsningsforslag som pdf laget av claes

Løsningsforslag fra NDLA

Oppgave 1

$A(r) = \pi r^2 \\ A'(r) = 2 \pi r \\ V(r) = \frac 43 \pi r^3 \\ V'(r) = 4 \pi r^2$

Oppgave 2

a)

$g(x)=3 \ln(x^2 -1) \\ g'(x)= 3 \cdot \frac{1}{x^2-1} \cdot 2x = \frac{6x}{x^2-1}$

b)

$h(x)= \frac{2x^2}{e^x} \\ h'(x) = \frac{4x \cdot e^x-2x^2e^x}{(e^x)^2} = \frac{2x(2-x)}{e^x}$

Oppgave 3

a)

$P(x)= x^3-6x^2+11x-6 \\ P(1)= 1^3 - 6 \cdot 1^2 + 11 \cdot 1 -6 =0$

b)

$ \quad( x^3-6x^2+11x-6) : (x-1) =x^2 - 5x + 6\\ -(x^3 -x^2) \\ \quad \quad -5x^2 \\ \quad \quad -(-5x^2 +5x) \\ \quad \quad \quad \quad \quad \quad 6x-6$

$x^2-5x+6=0 \\ x= \frac{5 \pm \sqrt{25-24}}{2} \\ x= 2 \vee x=3$

$P(x)=x^3-6x^2+11x-6 = (x-1)(x-2)(x-3)$

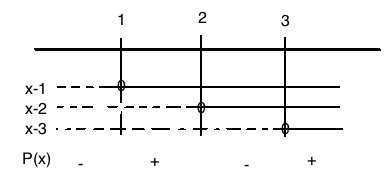
c)

$P(x) \leq 0$

$x \in < \leftarrow,1] \cup [2,3]$

Oppgave 4

$\ln(a^2b)-2 \ln a - \ln(\frac 1b) \\ = 2 \ln a + \ln b -2 \ln a - \ln 1 + \ln b \\= 2 \ln b$

Oppgave 5

f er kontinuerlig for $x \in <-1, 4>$

f er deriverbar for $x \in <-1, 2> \cup <2,4>$

Oppgave 6

$f(x)= x^3+6x^2-2 \\ f ' (x)= 3x^2 + 12x \\ f ' ' (x) = 6x+12$

vendepunkt;

$f ' ' (x)=0 \\ 6x+12=0 \\x = -2 \\ f(-2) = -8 + 24 -2 = 14 \\ ( -2, 14)$

Vendetangent;

$y= ax+b$

Stigningstall: $f ' (-2)= 3 \cdot 4 +12 \cdot (-2) = -12 $

Tangent:

$ y= -12x +b \\ 14 = -12 \cdot (-2) + b \\ b= 14 - 24 \\ b= -10 \\ y= -12x-10$

Oppgave 7

$\vec a = [2,3], \quad \vec b = [-6, 4], \quad \vec c = [3,11]$

a)

Dersom $ \vec a \perp \vec b$ så er skalarproduktet mellom vektorene lik null.

$[2,3] \cdot [-6,4] = 2 \cdot (-6) + 3 \cdot 4 = -12+12 =0 $ hvilket betyr at vektorene a og b står normalt på hverande.

b)

$ \vec c = k \vec a + t \vec b \\ [3, 11] = k[2, 3] + t[-6,4] \\ 3=2k - 6t \quad \wedge \quad 11 = 3k +4t \\ k= \frac 32 + 3t \quad \wedge \quad 11= 3( \frac 32 + 3t) + 4t \\ k= \frac 32 + 3t\quad \wedge\quad22=9+18t+8t \\ k= \frac 32 + 3t\quad \wedge\quad t= \frac 12 \\k=3\quad \wedge \quad t = \frac 12$

Oppgave 8

a)

b)

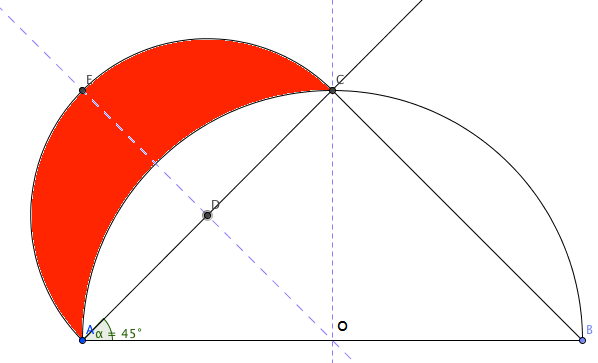
$\triangle AOC: A = \frac{r^2}{2}$

Kvartsirkel AOD: $A= \frac{\pi r^2}{4}$

Sirkelsegment ADC: $ A= \frac{\pi r^2}{4} - \frac{r^2}{2} =(\pi - 2) \frac{r^2}{4} $

Halvsirkel AEC: $ A= \frac 12 \pi (\frac{\sqrt{2r^2}}{2}) = \frac{\pi r^2}{4}$

Hippokratesmånen ( den røde flaten): $\frac{\pi r^2}{4} -(\pi - 2) \frac{r^2}{4} = \frac{r^2}{2}$

Vi ser at de to arealene er like store.

Oppgave 1

a)

Grafen til f skjærer x-aksen i x = -1 og er derfor delelig med (x+1), videre skjærer den i x = 1 og er derfor delelig med (-1). Den skjærer også i x = 3 og er derfor delelig med (x-3). En tredjegradsfunksjon kan maksimalt ha tre nullpunkter. Det har denne.

$f(x)= a(x+1)(x-1)(x-3) = a(x^2-1)(x-3)$

Konstanten a bestemmer "utslaget" til maksimums og minimumspunktene

$f(0)=12 \\ a(0-1) ( 0-3) =12 \\ a =4$

b)

$f(x)= 4x^3-12x^2-4x+12 \\ f ' (x) = 12x^2-24x-4 \\ f'(0) = -4 \\ y=ax+b \\ y= -4x+b \\ 12 = -4 \cdot 0 + b \\ b = 12 \\ y= -4x + 12 $

c)

Vi vet fra før at x = 0 er en løsning. Vi skal finne den andre og setter opp likningen:

$4(x-1)(x+1) (x-3 ) = -4 (x-3)$

Her kan vi dele på 4 på begge sider. Vi kan også dele på (x-3) dersom x = 3 ikke er en løsning av likningen. Dersom x=3 deler vi på null, og det gir ikke menming. Vi tester om x=3 er en løsning, og finner at det er tilfelle. Det andre skjæringspunktet blir derfor (3, 0).

Oppgave 2

a)

$\vec{OM_1} = \vec{OA} + \frac 12 \vec{AB} = [1,1] + \frac 12 [4,1] = [3, \frac 32]$

$\vec{OM_2} = \vec{OB} + \frac 12 \vec{BC} = [5,2] + \frac 12 [-2,2] = [4,3]$

$\vec{OM_3} = \vec{OA} + \frac 12 \vec{AC} = [1,1] + \frac 12 [2,3] = [2, \frac 52]$

b)

Parameterfremstilling for linjen gjennom A og $M_2$ :

Punkt A (1,1) og rettningsvektor [3, 2] gir:

<math>AM_2: \left[ \begin{align*} x &= 1+3t \\ y&=1+2t \end{align*}\right]</math>

Parameterfremmstilling for linjen gjennom C og $M_3$:

Punktet C (3, 4) og rettningsvektor $[ 0, \frac 52]$

<math>CM_3: \left[ \begin{align*} x &= 3 \\ y&=4- \frac 52s \end{align*}\right]</math>

c)

Søker skjæringen mellom de to linjene i oppgave b og får:

$1+3t = 3 \\ t = \frac 23 \\ x = 1+ 3 \cdot \frac 23 = 3 \\ y= 1+2 \cdot \frac 23 = \frac 73$

Dvs, T har koordinatene $(3, \frac 73)$.

Oppgave 4

a)

Pytagoras:

$x^2 + y^2 = 25 \\ y= \sqrt{25-x^2}$

Areal av rektangel :

$A = x \cdot y \\ A(x) = x \cdot \sqrt{25-x^2} \qquad x \in <0, 5>$

b)

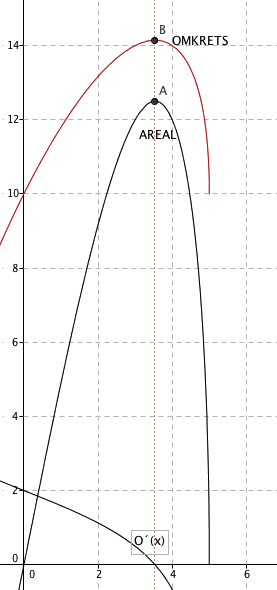
Fra Geogebra ser man at arealet er størst når x = 3,54. Da er $y= \sqrt{25- 3,54^2 }= 3,54 $. Arealet er størst når figuren er et kvadrat.

c)

Omkrets er to x pluss to y:

$O(x) = 2x + 2 \cdot \sqrt{25-x^2}$

Man observerer at O´(x) = 0 når x = 3,54. Altså er omkretsen også størst når figuren er et kvadrat.

Oppgave 5

6 røde kuler, 4 svarte kuler, totalt 10 kuler.

Trekker to kuler.

Definerer hendelser

A: to kuler med ulik farge

B: to kuler med lik farge.

a)

$P(A) = P(R) \cdot P(S) + P(S) \cdot P(R) = \frac{6}{10} \cdot \frac{4}{9} + \frac{4}{10} \cdot \frac{6}{9} = \frac{8}{15}$

b)

$P(B)=P(R) \cdot P(R) + P(S) \cdot P(S) = \frac{6}{10} \cdot \frac{5}{9} + \frac{4}{10} \cdot \frac{3}{9} = \frac{7}{15}$

Oppgave 6

$n^2 \cdot ( \frac{x}{n})^{\lg x} =x^2 \quad \quad n \in \N \\ (\frac{x}{n})^{\lg x} = (\frac{x}{n})^2 $

Likningen har en løsning når grunntallene på begge sider er lik en, dvs. x = n er en løsning.

Det er også

$\lg x = 2 \\ x= 100$