R1 2011 vår LØSNING: Forskjell mellom sideversjoner
| Linje 166: | Linje 166: | ||
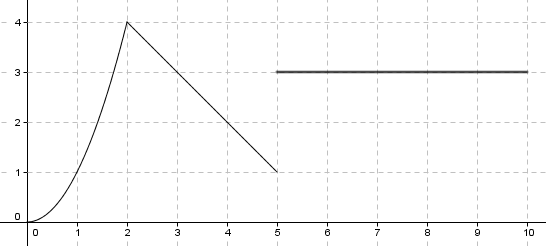
Det finnes uendelig mange funksjoner som passer til beskrivelsen. Det at en funksjon er kontinuerlig men ikke deriverbar betyr at den har et knekkpunkt. Den kan se slik ut: | Det finnes uendelig mange funksjoner som passer til beskrivelsen. Det at en funksjon er kontinuerlig men ikke deriverbar betyr at den har et knekkpunkt. Den kan se slik ut: | ||
[[File:6-r1-v2011]] | [[File:6-r1-v2011.png]] | ||
==Oppgave 7== | ==Oppgave 7== | ||
Sideversjonen fra 8. sep. 2013 kl. 17:30
DEL 1
Oppgave 1
a)
b)
1)
2)
c)
1)
Faktoriserer svaret fra divisjonen:
2)
d)
f(0) = 300
Ved begynelsen av utbruddet spruter vulkanen ut 300 tonn per time.
f'(10)=0 og f(10)= -10
Funksjonen når et ekstremalpunkt etter 10 timer, siden den deriverte er null. Den dobbelderiverte er negativ, hvilket betyr at den deriverte avtar og grafen vender sin hule side ned. Det betyr at vulkanen når et maksimum i utbruddet etter 10 timer.
e)
f)
g)
Avstanden fra linjen l til punktet P er lengden av vektoren som står normalt på rettningsvektoren til l og som går til P (eller motsatt).
l:
Rettningsvektor til l: [2,1]
P = (4,1)
Man finnet den t verdi som tilfredstiller kravet:
Vektoren blir da:
Lengden av vektoren er:
Avstanden fra l til P er kvadratroten av fem.
h)
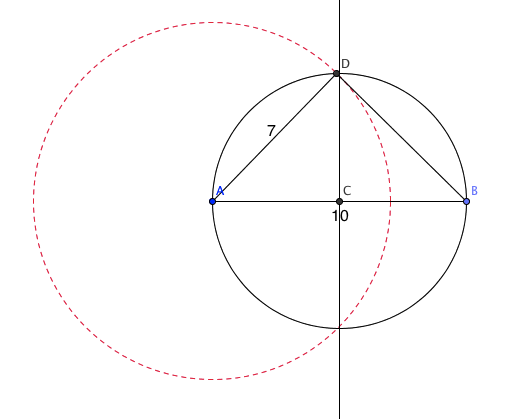
- Avsetter linjestykket AB, 10cm
- Finner midpunktet på AB og slår en sirkel med sentrum i midpunkt og pereferi i A og B.
- Slår en sirkel med radius 7cm, med sentrum i A
- D (skulle vært navngitt C) ligger der de to sirklene skjærer. Tegner trekanten.
Oppgave 2
a
Vinkelsummen i en trekant er 180 grader
DC = EC det betyr at trekanten er likebeint. Normalen fra C på DE deler u i to like store vinkler.
Det fører til at vinkel DEC.
b
Linjestykket BF går gjennom S, som er sentrum i den innskrevne sirkelen. BF deler vinkel v i to like store vinkler. Derfor er
Summen av de to vinklene er jo 180 grader.
c
Del 2
Oppgave 3
a
b
Setter inn for h, fra oppgave a:
c
Bredde:3,15cm, Lengde: 12,6 og høyde: 5,04 cm.
d
Oppgave 4
| Jente | Gutt | Total | |
| Matpakke | 180 | 100 | 280 |
| Ikke matpakke | 20 | 50 | 70 |
| Total | 200 | 150 | 350 |
a)
A er gutt og B er matpakke hver dag.
b)
Hendelsene er avhengige fordi sannsynligheten for B er forskjellig for sannsynligheten for B når A har inntruffet.
Oppgave 5
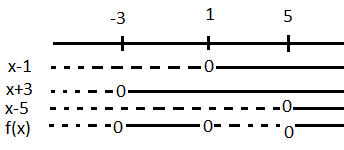
Oppgave 6
Det finnes uendelig mange funksjoner som passer til beskrivelsen. Det at en funksjon er kontinuerlig men ikke deriverbar betyr at den har et knekkpunkt. Den kan se slik ut:
Oppgave 7
a)
b)
c)
Skal bevise at
Bruker resultatet fra b: