1T 2013 vår LØSNING

Oppgaven som pdf

Diskusjon av denne oppgaven

Del I

Oppgave 1

$ \displaystyle \frac{ 750 000 }{0.005} = \frac{ 7.5 \cdot 10^5 }{ 0.5 \cdot 10^{-2} } = \frac{7+1/2}{1/2} \cdot 10^{5 - (-2)} = \left( 7 \cdot 2 + 1\right) \cdot 10^7 = 1.5 \cdot 10^8 $

Oppgave 2

$ \displaystyle \begin{align*} (1) 2x + 3y & = 7 \\ (2) 5x - 2y & = 8 \end{align*} $

Dersom vi ser på $2 \cdot (1) + 3 \cdot (2)$ ser vi at vi får likningen

$ \begin{align*} (4x + 6y) + (15x - 6y) & = 14 + 24 \\ 19x & = 19 + 19 \\ x & = 2 \end{align*} $

Alternativt kan innsetningsmetoden brukes, men da må en hanskes med brøker. Uansett setter vi inn $x$ verdien eksempelvis i $(1)$ finner vi at

$3y = 7 - 2x = 3$, så $y=1$ og $x=2$.

Oppgave 3

$ \displaystyle \frac{ x^2 - 16 }{ x^2 - 4x + 16 } = \frac{ x^2 - 16 }{ x^2 - 2 \cdot 4 \cdot x + 4^2} = \frac{ (x - 4)(x + 4) }{ (x-4)^2 } = \frac{ x + 4}{ x - 4 } $

Hvor det ble benyttet andre kvadratsetning $(a+b)^2 = a^2 + 2ab + b^2$.

Oppgave 4

Likningen for en rett linje er $y = ax + b$, her er stigningstallet gitt som

$ \displaystyle a = \frac{ 3 - 0 }{0 - 6} = - \frac{ 1 }{ 2 } $

slik at vi kan skrive

$ \displaystyle y = - \frac{1}{2}x + b $

for å bestemme $b$ så kan vi se at likningen må gå igjennom punktet $(0,3)$, slik at $x=0$ gir $y = 3$. Løser vi likningen for $b$ og setter inn fås

$ \displaystyle b = y + x/2 = 3 + \frac{1}{2} \cdot 0 = 3 \: . $

Så likningen for den rette linjen i koordinatsystemet er

$ \displaystyle y = \frac{1}{2} + 3\:. $

Oppgave 5

Skriver om alle uttrykkene $ (1/2)^0 = 1$ $ \sqrt[3]{27} = \sqrt[3]{3^2}=3$. $ \sqrt{20} = 2 \sqrt{5} > 2 \sqrt{4} = 4$. $ 1/9 - 3^{-2} = 0$. $ 0 \leq \sin 50^\circ \leq 1$. $ \lg 150 = \lg 10 + \lg 15 = 1 + \log 15 $.

Herfra så får vi i stigende rekkefølge

$ \displaystyle \frac{1}{9} - 3^{-2} < \sin 50^\circ < (1/2)^0 < \lg(150) < 27^{1/3} < \sqrt{20}. $

Siden $\lg 100 = 2$, og $\lg 10 = 1$, så er $1 < \log 15 < 2$ og sinus er per definisjon alltid mellom $0$ og $1$, her ble det da benyttet radianer.

Oppgave 6

Enten er begge kulene blå, eller så er begge kulene røde, summen er hva vi er ute etter.

$ \displaystyle (1) = P(\text{blå} \cap \text{blå}) = \frac{2}{5} \cdot \frac{1}{4} = \frac{1}{10} $

og

$ \displaystyle (2) = P(\text{rød} \cap \text{rød}) = \frac{3}{5} \cdot \frac{2}{4} = \frac{3}{10} $

Summen er da

$\displaystyle P(2 \cup 2) = \frac{4}{10} = \frac{2}{5} \approx 40 \percent $.

Oppgave 7

a) Legg merke til at

$ \begin{align*} f(x) = & -x^2 - 4x + 5 \\ = & -(x^2 -x + 5x - 5 ) \\ = & - [x(x-1) + 5(x-1)] \\ & = (x+5)(1-x) \end{align*} $

Nullpunktene er dermed $x=-5$ eller $x=5$. Alternativt fungerer og andregradsformelen, med marginalt mer regning.

b) Her har vi at

$f(x) = -(x^2 - 4x + 16) + 9 = 9 - (x+2)^2 $

Slik at $f(x)$ er maksimal når $x=-2$, altså vi fullfører kvadratet og legger merke til at $- (x+2)^2\leq 0$ for alle $x$, og den minste verdien denne delen kan ha er $0$ som skjer når $x=-2$. Alternativt fungerer derivasjon og så fortegnslinje eller drøfting av den dobbelderiverte. ($siden f(1)<0 så er $f(1)$ toppunkt$)

c) IKKE GJORT

d)

En tangentlinje er på formen $y = a(x - x_0) + b$, hvor vi har at $a = f'(1) = -2(-1) - 4 = -2$ og $x_0 = -1$, så tangentlinjen blir

$ y = -2(x + 1) + 8 = -2x +6 $

som ønsket.

Oppgave 8

a) Fra pytagoras har vi at siden $AOC$ er rett så er

$ AC^2 = AO^2 + OC^2 = r^2 + r^2 = 2 r^2 $

Siden lengden er positiv må $AC = \sqrt{2} \cdot r$, som ønsket.

b)

Arealet av $\triangle AOC$ er gitt som

$ \displaystyle A_1 = \frac{1}{2} r \cdot r = \frac{1}{2} r^2. $

Arealet av sirkelbuen med grunnlinje $AB$ er gitt som

$ \displaystyle A_S = \pi \cdot r^2 / 2 $.

Arealet av halvsirkelen med grunnlinje $AC$ er gitt som

$ \displaystyle A_C = \pi \cdot (AC/2)^2/2 = \pi \cdot r^2 / 4 = A_S / 2 $

Området mellom det blå, og trekanten er gitt som

$ \displaystyle A_M = A_S / 2 - A_1 $

Slik at for å finne arealet av det blå, kan vi regne ut arealet av halvsirkelen, og trekke fra det skaverte området. Da fås

$ \displaystyle A_B = AC - A_M = A_S/2 - ( A_S/2 - A_1) = A_1 $

som ønsket.

Del II

Oppgave 1

Her har vi følgelig en $30-60-90$ trekant. Da hypotenusen dobbelt så lang som den korteste kateten. Dette kan vi skrive som

$ \displaystyle 4^2 + x^2 = (2x)^2 \Rightarrow x = 4 \sqrt{3} \: . $

Slik at den korteste kateten er $4/\sqrt{3} \approx 2.3094$ og hypotenusen er $8/\sqrt{3} \approx 4.6188$

Oppgave 2

a) Her vil eksempelvis sinus-setningen være nyttig. Den sier at om $ABC$ er en trekant $\Delta ABC$, med interne vinkler $A, B, C$ og sider $a, b, c$ så er

$ \displaystyle \frac{ a }{ \sin A } = \frac{ b }{ \sin B } = \frac{ c }{ \sin C } $

bruker vi dette så har vi dette at

$ \displaystyle \begin{align*} \frac{ BD }{ \sin 60^\circ } & = \frac{ 5 }{ \sin 38.2^\circ } \\ BD & = \frac{ 5 }{ 2 } \sqrt{3} \cdot \sin 38.2^\circ \\ BD & \approx 7.0022 \end{align*} $

b) Her kan vi eksempelvis bruke at arealet av en trekant er gitt som $A = a \cdot b \cdot \sin (A) / 2 $.

Dersom vi ser først på trekant ABD først, har en at

$ \displaystyle \triangle ABD \approx \frac{1}{2} \cdot 5 \cdot 7 \cdot \sin( 180-60-38.2) \approx 17.32 $

For å finne arealet av den siste trekanten, kan eksempelvis herons formel benyttes. Her har en at $S \approx (4 + 6 + 7)/2 = 17/2$ hvor $S$ er halvparten av omkretsen til trekant $BCD$. Da er arealet

$ \triangle BCD = \sqrt{ S(S-a)(S-b)(S-c) } = \sqrt{ \frac{17}{2}\left( \frac{17}{2} - 4 \right) \left( \frac{17}{2} - 6 \right)\left( \frac{17}{2} - 7 \right) } = \frac{3}{4}\sqrt{255} \approx 11.977 $

Eller så kan vi bruke cosinussetningen til å først finne vinkel C.

$ \displaystyle \begin{align*} C & = \arccos \left( \frac{ a^2 + b^2 - c^2 }{ 2ab } \right) \\ & \approx \arccos \left( \frac{ 4^2 + 6^2 - 7^2 }{ 2 \cdot 4 \cdot 6 } \right) \\ & = \arccos \left( \frac{1}{16} \right) \\ & \approx 86.420 \end{align*} $

Også bruke sinussetningen slik at arealet kan skrives som

$ \triangle BCD \approx \frac{1}{2} \cdot 4 \cdot 6 \cdot \sin(86.420) \approx 11.97 $

samme som før.

Slik at det totalet arealet kan skrives som

$ \square ABCD = \Delta ABD + \Delta BCD \approx 29.297 $

Så arealet av figuren er omtrentlig $29$.

Oppgave 3

a)

Antall fargeblinde kan skrives som

$ \displaystyle \frac{8}{100} \cdot 4000 + \frac{1}{100} \cdot 6000 = 380 $

Slik at sannsynligheten for at en person er fargeblind (FB) er gitt som

$ \displaystyle \begin{align*} P(FB) & = \frac{ \text{ ønskelige } }{ \text{ mulige } } \\ & = \frac{ 380 }{ 4000 + 6000 } \\ & = \frac{ 19 }{ 500 } \\ & \approx 3.8 \: \percent \end{align*} $

Altså er sannsynligheten for at en tilfeldig person er fargeblind er $3.8 \percent$.

b) Antall kvinner som er fargeblinde er

$ \displaystyle \frac{1}{100} \cdot 6000 = 60 \:, $

slik at sannsynligheten for at en kvinne er fargeblind er gitt som

$ \displaystyle \begin{align*} P(FB \cap \text{Kvinne} ) & = \frac{ 60 }{ 380 } \\ & = \frac{ 3 }{ 19 } \\ & \approx 15.789 \: \percent \end{align*} $

Oppgave 4

a) Her bruker vi binomisk fordeling og får da

Definerer først sannsynligheten for at $X = k$, ønsker å flytte fra byen som

$ \displaystyle P(X = k) = \binom{100}{k} \left( \frac{1}{3} \right)^k \left( \frac{2}{3} \right)^{100 - k} $

Slik at sannsynligheten for at nøyaktig $30$ ønsker å flytte fra byen er gitt som

$ P(X = 30 ) \approx 0.067284 =6.7284 \: \percent $

Slik at sannsynligheten for at nøyaktig $30$ personer, ønsker å flytte fra byen er ca $6.7$ prosent.

b)

Her blir det bare å legge sammen alle sannsynlighetene mellom $30$ og $50$, geogebra eller en kraftig kalkulator klarer dette fint.

$ P(31 < X < 49) = \sum_{k=30}^{50} P(k) \approx 0.72303 $

Altså var sannsynligheten for at mellom $30$ og $50$ flyttet ut ca $72.3$ prosent.

Eventuelt går det og ann å tilnærme via normalfordelingen med $\mathcal{N}(33.333,4.7140)$, og få et godt overslag. Uansett viktig å legge merke til at mellom $30$ og $50$, betyr fra og med $31$ til og med $49$, og ikke fra $30$ til $50$.

Oppgave 5

a) La $M$ st for menn og $P$ for kvinner da har vi likningene

$ \begin{array}{rcrcr} M & + & K & = & 1000 \\ \frac{21}{100} M & + & \frac{16}{100} K & = & 1000/5 \end{array} $

Her deler vi på $5$, siden det bare var $1$ av $5$ som trente.

b) Begyner med løse øverste likning for $K$, da fås $K = 1000 - M$. Deretter ganges nederste likning med $100$, også settes inn opplysningen om $K$. Da fås

$ \begin{align*} \frac{21}{100} M + \frac{16}{100} K & = 200 \\ 21 M + 16 K & = 20 000 \\ 21 M + 16(1000 - M) & = 20 000 \\ 5 M + 16 000 & = 20 000 \\ M & = 800 \end{align*} $

Og tilsvarene så er $K = 1000 - 800 = 200$. Altså var det totalt sett $800$ menn og $200$ kvinner som deltok på undersøkelsen.

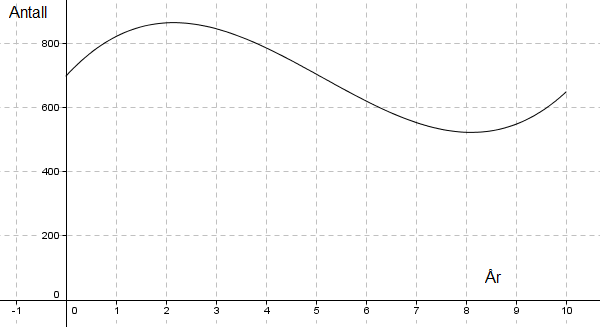
Oppgave 6

a)

b) Regner ut først ut første og andrederiverte

$ h(t) = 3.25 t^3 - 50 t^2 + 170 t + 700 $, derivasjon gir

$ h'(t) = 9.75 t^2 - 100 t + 170 $

$ h(t) = 19.5 t - 100 $

Via andregradsformel, eller datamaskin så er $h'(t)=0$ når

$ \displaystyle t = \frac{1}{39} \left( 200 \pm 2 \sqrt{3370} \right)\:, $

som gir

$ t_2 \approx 8.1052$ og $t_1 \approx 2.1412\:. $

Fra den dobbelderiverte ser en raskt at <math>h(t_2)>0</math> og <math>h(t_1)<0</math> slik at $t_1$ er et toppunkt. Tilslutt så er

$ h( t_1) = \frac{ 2172100 + 13480 \sqrt{3370} }{ 3463 } \approx 866.68\:, $

som selvsagt rundes opp til $867$ hjort. Altså var det maksimalt $867$ hjort i området.

c) Tegner figur. IKKE GJORT. Og ser fra figuren at

$h(t)>850$ når $1.4224 < t < 2.94526$

Denne ulikheten beskriver når det var flere enn $850$ hjort i området.

d)

$ h'(4) = -74 $

Det dette forteller oss er at i $199(4)$ var hjortebestanden synkende.

Oppgave 7

a) Her vil hypotenusen beskrive radius i sirkelen slik at pytagoras gir oss

$ r = \sqrt{a^2 + b^2} = \sqrt{5^2 + (2\cdot 5)^2} = 5 \sqrt{ 1 + 2^2 } = 5 \sqrt{5} \approx 11.180 $

b) her er $r = 10$ og sidelengden i trekanten vil være $2x/2x = x$. Den ene sidelengden kan da skrives som

$ b = \sqrt{r^2 - x^2} = \sqrt{100 - x^2} \:. $

Nå kan arealet av kvadratet skrives som

$A(x) = (b + b) \cdot (x + x) = 4x \cdot \sqrt{ 100 - x^2 } $

som ønsket.

c) La $B(x) = A(x)^2$, da er

$ B'(x) = \left( 16 x^2 (100 - x^2) \right)' = 3200 x - 64 x^3 = 64x (x^2 - 50) $

Slik at $A'(x)=0$ når $x=0$ eller $x^2 = 50$. Førstnevnte gir $A(0)=0$ som er et minimum mens

$ B(x^2=50) = 16 (50) \cdot 50 = 4 \cdot 10^4 $

og følgelig er

$A_{\text{max}} = \sqrt{ B(x^2=50) }= 2 \cdot 10^2 = 200$.

er et maksimum. Altså for $x = 2 \sqrt{5}$ siden $x$ må være positiv.

Oppgave 8

Litt kjapp regning gir oss at

$ \displaystyle \frac{c}{d} - \frac{c+7d}{d+7d} = \frac{7}{8} \left( \frac{c}{d} - 1\right) $

Om dette skal være lik $8$, så kan vi løse likningen med tanle på $c/d $ slik at en får $c/d = (7 + 8^2) / 7 = 71/7$, som en kan teste stemmer ved innsetning. Altså du kan sjekke om

$ \displaystyle \frac{71}{7} - \frac{71 + 7\cdot 7}{7 + 7\cdot 7} = 8 $