Trigonometri: Forskjell mellom sideversjoner
| Linje 87: | Linje 87: | ||
Eksempel 1: | Eksempel 1: | ||
Finn vinkel x: | Finn vinkel x: <br> | ||
<tex> tan 30^\circ = \frac{a}{5}\Rightarrow a = 5tan 30^\circ = 5 \cdot 0,58 = 2,9 </tex> | <tex> tan 30^\circ = \frac{a}{5}\Rightarrow a = 5tan 30^\circ = 5 \cdot 0,58 = 2,9 </tex> | ||
| Linje 107: | Linje 107: | ||
Vi har så langt sett på definisjoner for de trigonometriske funksjonene når vinkelen er mindre enn 90 grader. Vi har behov for å definer de trigonometriske funksjonen for vinkler større enn 90º og for vinkler mindre enn 0º. | Vi har så langt sett på definisjoner for de trigonometriske funksjonene når vinkelen er mindre enn 90 grader. Vi har behov for å definer de trigonometriske funksjonen for vinkler større enn 90º og for vinkler mindre enn 0º. | ||
== Enhetssirkelen == | == Enhetssirkelen == | ||
Sideversjonen fra 11. mai 2009 kl. 09:22
Trigonometri kan blant annet brukes til å finne vinkler i trekanter og lengen av sidekanter i trekanter. De trigonometriske funksjonene vi skal befatte oss med her er tangens, sinus og cosinus. På lommeregnere vil disse funksjonene være merket tan, sin og cos. Vi får også bruk for de omvendte funksjonene. Disse er merket <tex>tan^{-1}</tex>, <tex>sin^{-1}</tex>, og <tex>cos^{-1}</tex>, .
Formlikhet
En trekant er formlik med en annen trekant dersom vinklene i begge trekantene er like store. Dersom vi skal påvise at to trekanter er formlike må vi vise at to og to av vinklene i trekantene er identiske (den tredje gir seg da selv).
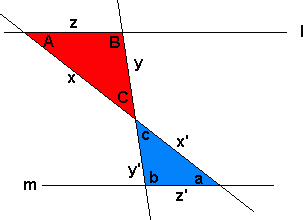
I denne figuren er rød trekant formlik blå trekant fordi linjene l og m er parallelle og fordi vinkel C og c er toppvinkler. Vinkel A = a, B = b og C =c. Vi har følgende forhold mellom lengdene på sidekantene i trekantene:
<tex> \frac{x}{y}= \frac{x'}{y'}= </tex> eller
<tex> \frac{z'}{x'}= \frac{z}{x}= </tex>
Uttrykkene over kalles for proporsjoner og leses "Forholdet mellom to sider i den ene trekanten er lik forholdet mellom tilsvarende sider i den andre trekanten". Dette gjelder bare når trekantene er formlike.
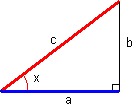
Rettvinklet trekant
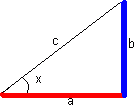
En rettvinklet trekant består av to kateter og en hypotenus. Vi kaller det katetet som sammen med hypotenusen danner den aktuelle vinkelen i trekanten for "hosliggende katet". Det andre katetet blir "motstående katet".
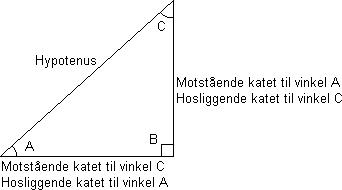
I en rettvinklet trekant, for vinkler mindre enn 90 grader, gjelder:
Tangens
Tangens til den spisse vinkel defineres som forholdet mellom motstående katet og hosliggende katet til vinkelen x.
<tex> Tan x = \frac{b}{a}</tex>
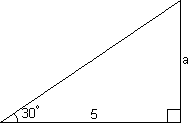
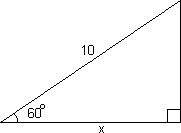
Eksempel 1:
La oss tenke oss en rettvinklet trekant der den ene vinkelen er 30 og hosliggende katet er 5 enheter. Vi kan da bruke tangensfunksjonen til å finne lengden av det andre katetet.
<tex> tan 30^\circ = \frac{a}{5}\Rightarrow a = 5tan 30^\circ = 5 \cdot 0,58 = 2,9 </tex>
Lengden av a blir da; a = 2,9 enheter
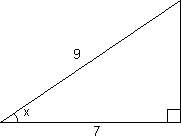
Eksempel 2:
Dersom vi kjenner lengden av begge katetene kan tangens brukes til å finne vinklene i trekanten.
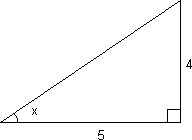
<tex> tan x = \frac{4}{5}=0,8 \Rightarrow x = tan^{-1}0,8=38,7^\circ </tex>
Sinus
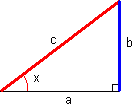
Sinus til vinkelen x defineres som forholdet mellom motstående katet til x og hypotenusen.
<tex> Sin x = \frac{b}{c}</tex> Eksempel 1: <tex> tan 30^\circ = \frac{a}{5}\Rightarrow a = 5tan 30^\circ = 5 \cdot 0,58 = 2,9 </tex> Dersom vi kjenner hypotenusen og motstående katet til vinkel x, finner vi vinkel x slik:
Eksempel 2:
<tex> tan 30^\circ = \frac{a}{5}\Rightarrow a = 5tan 30^\circ = 5 \cdot 0,58 = 2,9 </tex>
Lengden til hypotenusen er 7,1 enheter.
Cosinus
Cosinus til vinkelen x defineres som forholdet mellom hosliggende katet og hypotenusen.
<tex> tan 30^\circ = \frac{a}{5}\Rightarrow a = 5tan 30^\circ = 5 \cdot 0,58 = 2,9 </tex>
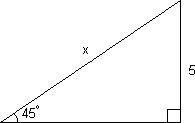
Eksempel 1:
Finn vinkel x:
<tex> tan 30^\circ = \frac{a}{5}\Rightarrow a = 5tan 30^\circ = 5 \cdot 0,58 = 2,9 </tex>
Eksempel 2:
Finn lengden av katetet x:
<tex> tan 30^\circ = \frac{a}{5}\Rightarrow a = 5tan 30^\circ = 5 \cdot 0,58 = 2,9 </tex>
Lengden til katetet x er 5 enheter.
26.6
Vi har så langt sett på definisjoner for de trigonometriske funksjonene når vinkelen er mindre enn 90 grader. Vi har behov for å definer de trigonometriske funksjonen for vinkler større enn 90º og for vinkler mindre enn 0º.
Enhetssirkelen
For å kunne definere de trigonometriske funksjonene for vinkler større enn 90 grader introduserer vi enhetssirkelen. Enhetssirkelen har sentrum i origo og radius en.
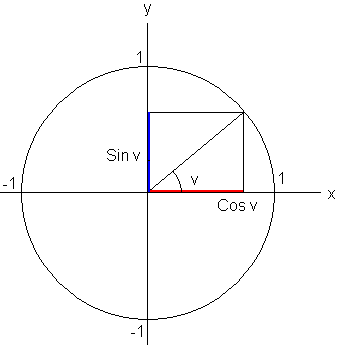
Man definerer cosinus til vinkelen v som x-koordinaten og sinus til v som y-koordinaten.
26.8
Sinus [0,180]
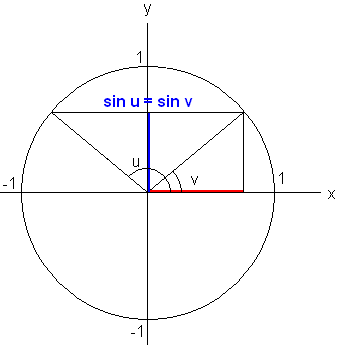
To vinkler som til sammen blir 180 grader kalles supplementvinkler. På grunn av symmetri om y-aksen har man at
Sinus til en vinkel i 1. og 2. kvadrant er en positiv verdi.
Dersom vinkelen ligger i 3. eller 4. kvadrant er sinus negativ.
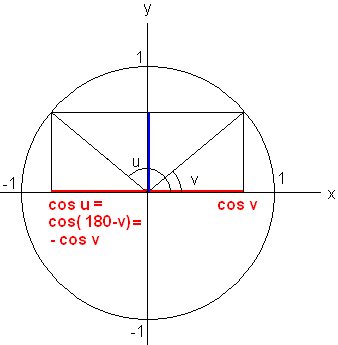
Cosinus [0,180]
Cosinus er positiv i første kvadrant, for vinkler opp til 90 grader. I andre kvadrant er cosinus negativ.
Dersom vinklene u og v er supplementvinkler er:
Cos u = cos (180 - v) = - cos v
arealsetningen
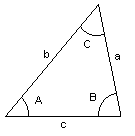
Når sidene i en trekant har lengden b og c, og vinkelen mellom dem er A, Så er arealet T av trekanten gitt ved:
T = 1/2 bc SinA
<tex> T= \frac12bc \cdot SinA </tex>
eller
<tex> T= \frac12ac \cdot SinB </tex>
eller
<tex> T= \frac12ab \cdot SinC </tex>
sinussetningen
I en trekant med vinkler A, B og C og sider a, b og c er følgende forhold gitt:
<tex> \frac{SinA}{a} =\frac{SinB}{b} = \frac{SinC}{c}</tex>
eller
<tex> \frac{a}{SinA} =\frac{b}{SinB} = \frac{c}{SinC}</tex>
cosinussetningen
I en trekant med vinkler A, B og C og sider a, b og c (a motstående til A osv.) er

<tex>a^2 =b^2+ c^2 - 2bc \cdot cosA </tex>
eller
<tex>b^2 =a^2+ c^2 - 2ac \cdot cosB </tex>
eller
<tex>c^2 =a^2+ b^2 - 2ab \cdot cosC </tex>
Setningen kalles også den utvidede pytagoreiske læresetning.
Absolutt Vinkelmål
I kapitlene om geometri har du lært at vinkler måles i grader. Vi kan også måle vinkler i en enhet vi kaller for radianer. En sirkel består av 360 grader. Radianer tar utgangspunkt i forholdet mellom buen og radien. Vinkelen, målt i radianer, er:
Dersom lengden av radien er 1, vil vinkelen som måler en radian spenne over en buelengden med lengde 1:
Formelen for omkretsen av en sirkel er O = 2πr. O tilsvarer da buelengden i hele sirkelen. Det betyr at vinkelen på 360 tilsvarer følgende i radianer:
Fra dette følger at sammenhengen mellom radianer og grader er:
Vi har følgende sammenhenger mellom grader og radianer: