1T 2011 vår LØSNING

Del 1

Oppgave 1

a)

1) <tex>36 200 000 = 3.62 \cdot 10^7</tex>

2) <tex>0.034 \cdot 10^{-2} = 3.4 \cdot 10^{-4}</tex>

b)

<tex>x^2 + 6x = 16 \quad \Leftrightarrow \quad x^2 + 6x - 16 = 0</tex>

Ved fullstendig kvadrat:

<tex>\begin{align} x^2 + 6x - 16 &= x^2 + 6x + \Big( \frac{6}{2} \Big)^2 - 16 - \Big( \frac{6}{2} \Big)^2 \\ &= x^2 + 6x + 9 - 25 \\ &= (x+3)^2-5^2 \\ &= (x + 3 - 5)(x + 3 + 5) \\ &= (x - 2)(x + 8) \\ &= 0 \end{align} </tex>

<tex>x = 2 \quad \vee \quad x = -8</tex>

Eller med abc-formelen:

<tex>x = \frac{-6 \pm \sqrt{6^2 - 4\cdot 1 \cdot (-16)} }{2 \cdot 1} = \frac{-6 \pm \sqrt{100}}{2} = -3 \pm 5</tex>

<tex>x = 2 \quad \vee \quad x = -8</tex>

c)

Begynner med å faktorisere uttrykket:

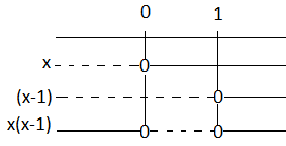
<tex>x^2-x<0 \Leftrightarrow x(x-1)<0 </tex>

Tegner så fortegnsskjema:

<tex>x \in <0,1></tex>

d)

1) E

2) C

3) J

4) B

5) G

6) H

e)

<tex>\text{lg}(2x - 1) = 2</tex>

<tex>2x - 1 = 10^2</tex>

<tex>2x = 101</tex>

<tex>x = \frac{101}{2}</tex>

f)

1)

Lager krysstabell, setter inn verdiene fra oppgaven og regner ut de andre slik at tabellen blir fullstendig:

	Sommerjobb S	Ikke sommerjobb <tex>\bar{S}</tex>	Sum
Ferie F	<tex>10</tex>	<tex>4-2=2</tex>	<tex>10+2=12</tex>
Ikke ferie <tex>\bar{F}</tex>	<tex>16-10=6</tex>	<tex>2</tex>	<tex>6+2=8</tex>
Sum	<tex>16</tex>	<tex>20-16=4</tex>	<tex>20</tex>

2)

I tabellen fant vi at 12 elever skal på ferie, og fra oppgaveteksten vet vi at det er 20 elever i klassen. Da blir sannsynligheten for at en tilfeldig valgt elev i klassen skal på ferie <tex>\frac{12}{20}=\frac 35=0,60=60 \percent</tex>

Oppgave 2

a)

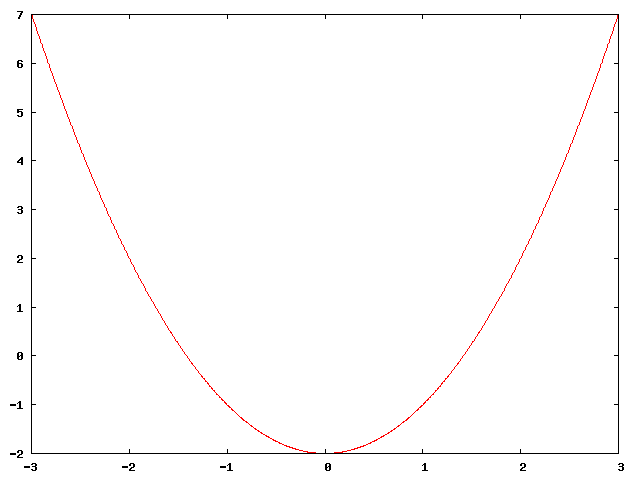
b)

Sekanten er gitt ved

<tex>\begin{align}S(x) &= f(0) + \frac{f(2) - f(0)}{2-0}(x-0) \\ &= -2 + \frac{(2^2-2)-(-2)}{2}x \\ &= 2x-2\end{align}</tex>

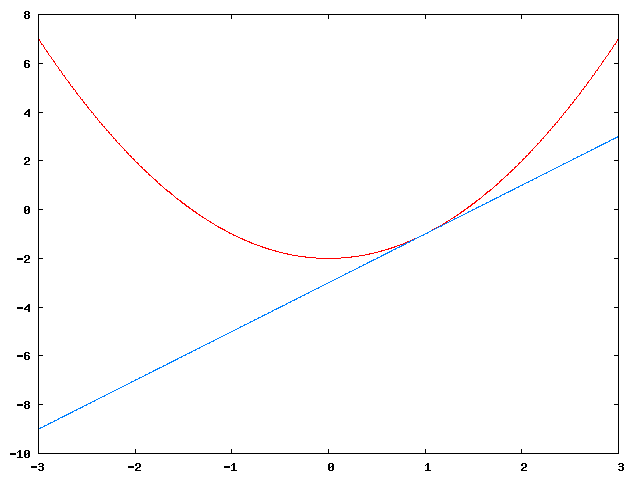
c)

Tangenten er gitt ved

<tex>\begin{align} T(x) &=f(1) + f^{\prime}(1)(x-1) \\ &= 1^2-2 + 2(x-1) \\ &= 2x - 3 \end{align} </tex>

Der det er brukt at <tex>f^{\prime}(x) = 2x</tex>.

Oppgave 3

a)

Her er <tex>AB=1</tex>, og <tex>BE=\frac 12 \cdot BC= \frac 12\cdot 1=\frac 12</tex>. Lengden av <tex>AE</tex> blir da:

<tex>AE^2=AB^2+BE^2 \Leftrightarrow AE=\sqrt{AB^2+BE^2}=\sqrt{1^2+\left( \frac 12\right)^2}=\sqrt{(\frac 22)^2+\left( \frac 12\right)^2}=\sqrt{\frac {2^2}{2^2}+\frac {1^2}{2^2}}=\sqrt{\frac{4+1}4}=\sqrt{\frac{5}4}=\frac {\sqrt{5}}{\sqrt{4}}=\frac{\sqrt 5}2</tex>

b)

Areal av trekant AEF:

<tex> A = 1 - 2\frac{1\cdot \frac{1}{2}}{2} - \frac{(\frac{1}{2})^2}{2} = \frac 88 - \frac 48 - \frac 18 = \frac 38</tex>

c)

<tex>A= \frac12 abSinC \\ \frac 38 = \frac 12 \cdot \frac{\sqrt5}{2} \cdot \frac{\sqrt5}{2}SinA \\ \frac38 = \frac 58 SinA \\Sin A = \frac35</tex>

Del 2

Oppgave 4

a)

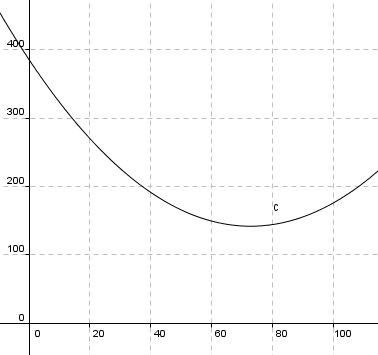
b)

Grafisk:

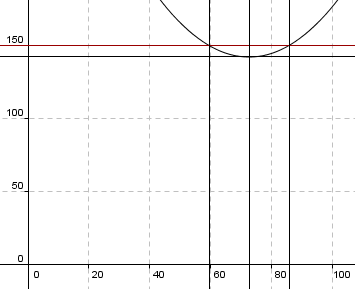
1) Man ser fra grafen at når bilen slipper ut 150g/km er farten enten 60 km/t eller 86km/t.

2) Man ser fra grafen at det laveste utslippet er 142g/km, da er farten 73km/t

Ved regning:

1)

<tex>f(x)=150 \\ 0,046x^2-6,7x + 386 = 150 \\ 0,046x^2-6,7x + 236 = 0 \\ x = \frac{6,7 \pm \sqrt{6,7^2-4 \cdot 0,046 \cdot 236}}{2 \cdot 0,046} = \frac{6,7 \pm 1,21}{0,092}\\ x =59,7 \quad \vee \quad x = 86</tex>

2)

<tex>f'(x)=0,092x-6,7 \\ f'(x)=0 \\ 0,092x - 6,7 = 0 \\ x = 72,8 </tex>

c)

<tex>f(70) = 0.046 \cdot 70^2 - 6,7 \cdot 70 +386 = 142,4 </tex>

På en halv time i 70 km/t beveger bilen seg 35km.

Utslippet blir da 4984 gram, altså ca 5kg.

Oppgave 5:

a)

<tex> \frac{1,2}{1,6} = \frac {x}{12} \\ x= \frac {x \cdot 1,6}{12 \cdot 1,2} \\ x = 9</tex>

b)

<tex> tan \alpha = \frac {9}{12} \\ \alpha = tan^{-1} ( \frac {9}{12}) \\ \alpha = 36,9^{\circ}</tex>

c)

Legg planken på det flate underlaget slik at den stikker en meter ut over kanten. Mål avstanden fra tuppen på planken til bakken. Den verdi du finner vil da være tan u.

d)

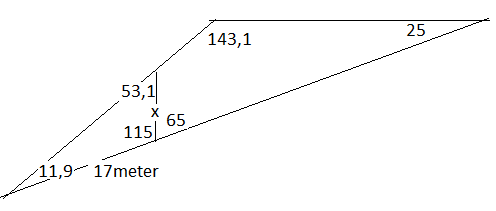
Treets høyde:

<tex> \frac{17m}{sin 53,1} = \frac {x}{sin 11,9} \\ x= 4,4m</tex>

Oppgave 6:

a)

1)Det var ca. 15 grader. (fra graf der den krysser y aksen)

2)Det ble varemet i ca. 5 minutter og var 90 grader når de ble satt i kjøleskapet.

b)

Grafen for oppvarming, fra null til fem minutter ser ut som en rett linje.:

f(x) = 15x + 15

f(x)= 100

15x + 15 = 100

Det vil ta 5 minutter og 40 sekunder.

c)

<tex> f(x) = 115,82 \cdot 0,94^x x \geq \\ f(x)> 60 \\ 115,82 \cdot 0,94^x + 5 > 60 \\ 0,94^x > 0,4748 \\ xlg0,94 > lg 0,4748 \\ x < \frac{lg 0,4748}{lg 0,94} \\ x \in [5,12> </tex>

d)

5 grader.

Oppgave 7:

a)

LARS	BÅRD	Resultat
papir	papir	U
saks	saks	U
stein	stein	U
stein	saks	V - Lars
papir	stein	V - Lars
saks	papir	V - Lars
papir	saks	V - Bård
stein	papir	V - Bård
saks	stein	V - Bård

b)

Fra tabellen i a ser man at det er tre gunstige utfall for at Bård vinner, av ni mulige utfall. 3/9 = 1/3. Dvs. P(B) = 1/3.

Oppgave 8:

a)

<tex>AC=BD \wedge AB=CD \wedge AD = BC \\ AC \cdot BC = AB \cdot CD + AD \cdot BC \\ AC^2 = AB^2 + AD^2 </tex>

Det er Pytagoras setning.

b)

Likesidet trekant: AB = BC = AC

<tex>AB \cdot PC = AP \cdot BC + PB \cdot AC \\ AB \cdot PC = AP \cdot AB + PB \cdot AB \\ PC= PA + PB</tex>

Det er tre forsøk av tre muligheter hver gang: <tex>3^3=27</tex>