1T 2011 høst LØSNING: Forskjell mellom sideversjoner
| Linje 127: | Linje 127: | ||
== c) == | == c) == | ||
== Oppgave 8. == | |||
== a) == | |||
== b) == | |||
== c) == | |||
== d) == | |||
Sideversjonen fra 3. okt. 2012 kl. 06:59
DEL EN
Oppgave 1:
a)
<tex> \frac{x^2-25}{x^2+10x+25} = \frac{(x+5)(x-5)}{(x+5)(x+5)} = \frac{x-5}{x+5}</tex>
b)
<tex> 3^{2x-1} = 1 \ 3^{2x-1} = 3^0 \ 2x-1 = 0 \ x= \frac 12</tex>
c)
<tex> \frac{a^{\frac 14} \sqrt a}{(a^{\frac 34})^3 \cdot a^{-2}}= a^{\frac 14 + \frac 24 - \frac 94 + \frac 84} = a^{\frac 12} = \sqrt a </tex>
d)
<tex> A= \frac {gh}{2} \6= \frac {5h}{2} \ h = \frac {12}{5} </tex>
e)
Ser fra figuren at:
<tex> f(x) \leq 0 \quad \quad \quad x \in <\leftarrow,1] \cup [3, \rightarrow> \ f(x) > g(x) \quad \quad x \in <0,5></tex>
f)
<tex>tanC =2 \ 2= \frac{AB}{AC} \ AC = 1,5 </tex>
g)
3 Blå, 2 røde, 1 grønn. Totalen er 6.
1) <tex> \frac 56 \cdot \frac 45 = \frac 23 </tex>
2) <tex> \frac 36 \cdot \frac 25 + \frac 26 \cdot \frac 35 = \frac 25 </tex>
h)
<tex> f(x)=x^2+1 \ \lim_{\Delta x\to\0}\quad\frac{f(x+ \Delta x) - f(x)}{\Delta x} \ \lim_{\Delta x\to\0}\quad\frac{(x+ \Delta x)^2 +1 - (x^2+1)}{\Delta x} \ \lim_{\Delta x\to\0}\quad\frac{x^2+2x \Delta x +( \Delta x)^2+1-x^2-1 }{\Delta x} \ \lim_{\Delta x\to\0}\quad\frac{2x \Delta x +( \Delta x)^2}{\Delta x} \ \lim_{\Delta x\to\0}\quad\frac{\Delta x(2x + \Delta x)}{\Delta x} \ \lim_{\Delta x\to\0} \quad 2x + \Delta x = 2x</tex>
Oppgave 2
a)
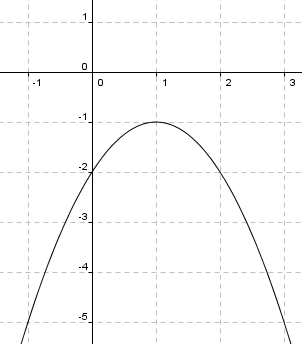
<tex>f(x) = -x^2+2x-2</tex>
Desom ingen nullpunkter må
<tex>b^2-4ac <0 \ 2^2-4 \cdot(-1) \cdot (-2) =-4</tex>
Dvs. ingen nullpunkter
b)
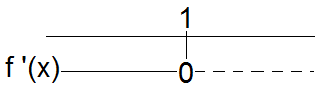
<tex>f'(x) = -2x+2 \ f'(x)=0 \ -2x+2 =0 \ x=1</tex>
Ekstremalpunkt: f(1) = -1, dvs. man har et maksimum i punktet (1,-1).
c)
f har en tangent i (2,-2)
Stigningstall: f'(2)= -2
y=-2x+b
-2 = -4 + b
b=2
Likning for tangent: y = -2x +2
Oppgave 3
a)
Tilnærmet: F = 2C + 30
Eksakt: 5F = 9C + 160
100 grader celsius er tilnærmet F = 230, altså 230 Farenheit. Eksakt er det:
<tex> 5F = 9C +160 \ 5F = 900 + 160 \ F= 212</tex>
Man observerer at forskjellen er 18 grader og at den tilnærmede metoden viser for mye ved 100 grader celsius.
b)
<tex> \left[F=2C+30 \ 5F = 9C +160 \right] \ \left[F=2C+30 \ 5(2C+30) = 9C +160 \right] \C = 10 \wedge F = 50</tex>
Det betyr at tilnærmingen er helt riktig når temperaturen er 10C (50F), men at den blir mer og mer unøyaktig når temperaturen fjerner seg fra 10 grader celsius.
DEL TO