1T 2012 vår LØSNING: Forskjell mellom sideversjoner
| Linje 52: | Linje 52: | ||
Fra diagrammet ser man at sannsynligheten for at eleven spiller håndball når man vet at eleven spiller fotball er seks femtenedeler. | Fra diagrammet ser man at sannsynligheten for at eleven spiller håndball når man vet at eleven spiller fotball er seks femtenedeler. | ||
<p></p> | <p></p> | ||
<tex>P( | <tex>P(haandball | fotball) = \frac {6}{15}</tex> | ||
Sideversjonen fra 31. mai 2012 kl. 06:28
Opgave 1
a)
1) <tex> 8+2 \cdot 3 - 3^2 - (10-12)^2 = 8 + 6 - 9 -4 =1</tex>
2)
<tex> \frac{9^{\frac 12} \cdot 3^{-3}}{(3^{-2})^3} = \frac{(3^2)^{\frac 12} \cdot 3^{-3}}{3^{-6}} = 3^{1-3+6} =3^4 = 81 </tex>
b)
<tex>5,5 \cdot 10^5 \cdot 6,0 \cdot 10^6 = 5,5 \cdot 6,0 \cdot 10^{11} =33,0 \cdot 10^{11} = 3,3 \cdot 10^{12} </tex>
c)
<tex>\left[{ x+2y =16 \\ 3x-y=6 }\right] \\ \left[{ x =16-2y \\ 3(16-2y)-y=6 }\right] \\ \left[{ x =16-2y \\ 48-6y-y=6 } \right] \\ \left[{ x =16-2y \\ y=7 } \right] \\ \left[{ x = 2 \\ y=7 } \right] </tex>
d)
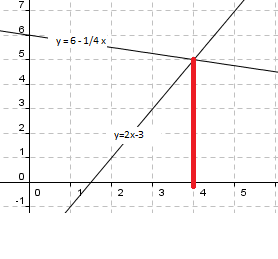
<tex>2x-3=6- \frac 14x</tex>
Grafisk løsning
Man observerer at: x = 4
e)
<tex>-x^2-x+13 \geq 0</tex>
Faktoriserer (abc-formelen) og får:
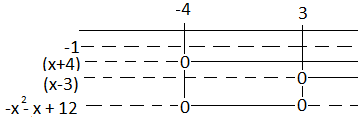
<tex>-(x+4)(x-3) \geq 0</tex>
Fortegnsskjema:
<tex> x \in [-4,3]</tex>
f)
Man ser at uttrykket i teller er det samme som uttrykket i e.
<tex>\frac{-x^2-x+12}{x^2-9} = \frac{-(x+4)(x-3)}{(x+3)(x-3)} = - \frac{x+4}{x+3}</tex>
g)
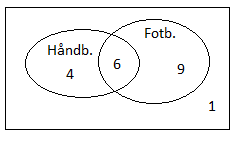
I et Venndiagram ser situasjonen slik ut:
Fra diagrammet ser man at sannsynligheten for at eleven spiller håndball når man vet at eleven spiller fotball er seks femtenedeler.
<tex>P(haandball | fotball) = \frac {6}{15}</tex>