R1 2011 vår LØSNING: Forskjell mellom sideversjoner
| Linje 44: | Linje 44: | ||
== f) == | == f) == | ||
<tex> \frac {2x+10}{x^2-25} + \frac {x}{x+5} - \frac {2}{x-5}= \\ \frac {2x+10}{(x+5)(x-5)}\frac {x(x-5)}{(x+5)(x-5)}\frac {2(x+5)}{(x-5)(x+5)}\frac {}{}\frac {}{}\frac {}{}\frac {}{}\frac {}{}\frac {}{}</tex> | <tex> \frac {2x+10}{x^2-25} + \frac {x}{x+5} - \frac {2}{x-5}= \\ \frac {2x+10}{(x+5)(x-5)} + \frac {x(x-5)}{(x+5)(x-5)} - \frac {2(x+5)}{(x-5)(x+5)} = \\ \frac {}{}\frac {}{}\frac {}{}\frac {}{}\frac {}{}\frac {}{}</tex> | ||
== g) == | == g) == | ||
Sideversjonen fra 13. mar. 2012 kl. 10:37
DEL 1
Oppgave 1
a)
<tex>O(x)= \frac{500}{x} + 8x^2 \\ O(x) = 500x^{-1} + 8x^2 \\ O'(x) = -500x^{-2}+ 16x = \frac{-500}{x^2} + 16x = \frac{-500 +16x^3}{x^2}</tex>
b)
1)
<tex>f(x)= 3ln(2x) \\ f'(x) = 3 \cdot \frac{1}{(2x)}\cdot 2 = \frac {6}{2x} = \frac 3x</tex>
2)
<tex>g(x) = 3x \cdot e^{x^2} \\ g'(x) = 3e^{x^2}+3x \cdot 2x \cdot e^{x^2} = (3+6x^2)e^{x^2}</tex>
c)
1)
<tex>f(x)= x^3-3x^2-13x+15 \\ f(1)= 1-3-13+15 = 0 \\ \quad(x^3-3x^2-13x+15):(x-1)= x^2-2x-15 \\-(x^3-x^2) \\ \quad \quad\quad \quad \quad-2x^2-13x \\\quad \quad\quad -(-2x^2+2x)\\\quad \quad\quad \quad\quad \quad\quad \quad \quad \quad-15x+15 \\ \quad \quad \quad\quad \quad \quad\quad\quad -(-15x+15) \\\quad \quad\quad \quad \quad\quad \quad\quad \quad \quad\quad \quad\quad \quad \quad\quad \quad\quad \quad \quad 0 </tex>
Faktoriserer svaret fra divisjonen:
<tex>x= \frac{2 \pm \sqrt{4+60}}{2}= \frac{2 \pm 8}{2}\\ x=-3 \vee x= 5</tex>
<tex>f(x) = (x-1)(x+3)(x-5)</tex>
2)
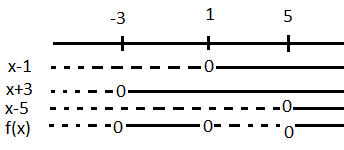
<tex>f(x)\leq 0</tex>
<tex>x \in < \leftarrow, -3] \cup [1,5]</tex>
d)
f(0) = 300
Ved begynelsen av utbruddet spruter vulkanen ut 300 tonn per time.
f'(10)=0 og f(10)= -10
Funksjonen når et ekstremalpunkt etter 10 timer, siden den deriverte er null. Den dobbelderiverte er negativ, hvilket betyr at den deriverte avtar og grafen vender sin hule side ned. Det betyr at vulkanen når et maksimum i utbruddet etter 10 timer.
e)
<tex>lg(a^2b)+lg(ab^2)+lg(\frac{a}{b^3})= \\ lga^2 + lgb + lga + lgb^2 + lga - lgb^3 = \\ 2lga + lgb + lga + 2lgb + lga - 3lgb = 4 lga</tex>
f)
<tex> \frac {2x+10}{x^2-25} + \frac {x}{x+5} - \frac {2}{x-5}= \\ \frac {2x+10}{(x+5)(x-5)} + \frac {x(x-5)}{(x+5)(x-5)} - \frac {2(x+5)}{(x-5)(x+5)} = \\ \frac {}{}\frac {}{}\frac {}{}\frac {}{}\frac {}{}\frac {}{}</tex>
g)
h)
Oppgave 2
a
Vinkelsummen i en trekant er 180 grader
<tex>90^{\circ}+u+v = 180^{\circ} \Rightarrow u+v= 90^{\circ}</tex>
DC = EC det betyr at trekanten er likebeint. Normalen fra C på DE deler u i to like store vinkler.
Det fører til at vinkel DEC.
<tex>\angle DEC +90^{\circ}+ \frac u2 = 180^{\circ} \Rightarrow \quad \angle DEC= 90^{\circ}-\frac u2 </tex>
b
Linjestykket BF går gjennom S, som er sentrum i den innskrevne sirkelen. BF deler vinkel v i to like store vinkler. Derfor er
<tex>\angle FBE = \frac v2</tex>
<tex>\angle BEF= 90^{\circ} + \frac u2 \quad fordi \quad \angle DEC = 90^{\circ}- \frac u2 </tex>
Summen av de to vinklene er jo 180 grader.
c
<tex>x+ \angle FBE + \angle BEF = 180^{\circ} \\ x+ \frac u2 + 90^{\circ} + \frac u2 = 180^{\circ} \\ 2x+v+180^{\circ} + u = 360^{\circ} \\ 2x+v+u = 180^{\circ} \\ 2x+v+(90-v) = 180^{\circ} \\ x= 45^{\circ} </tex>