Formlik: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
Ingen redigeringsforklaring |
||
| Linje 12: | Linje 12: | ||
[[Bilde:Form3.png]]<p></p> | [[Bilde:Form3.png]]<p></p> | ||
Forholdet mellom koresponderende sider i to fomlike trekanter er konstant. Dersom en trekant har siden A, B og C og en annen trekant har koresponderende sider a, b og c er <tex> \quad \frac Aa = \frac Bb = \frac Cc = k</tex> | Forholdet mellom koresponderende sider i to fomlike trekanter er konstant. Dersom en trekant har siden A, B og C og en annen formlik trekant har koresponderende sider a, b og c er <tex> \quad \frac Aa = \frac Bb = \frac Cc = k</tex> | ||
---- | ---- | ||
[[kategori:lex]] | [[kategori:lex]] | ||
Sideversjonen fra 2. sep. 2011 kl. 12:05
To formlike figurer har samme form, men ikke samme størrelse. Forholdet mellom de korresponderende sidene i formlike figurer er konstant.
To trekanter er formlike dersom du greier å vise at et av kravene nedenfor er oppfyllt (da er de to andre også oppfyllt):
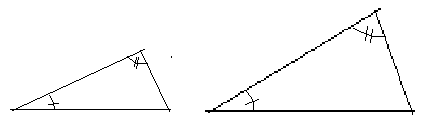
1. To vinkler i den ene trekanten er like store som de korresponderende vinkler i den andre trekanten.
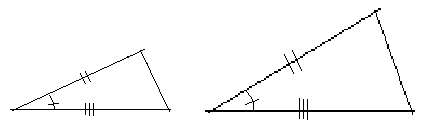
2 Forholdet mellom to par koresponderende sider i trekantene er like og vinkelen mellom sidene i de respektive trekanter er den samme.
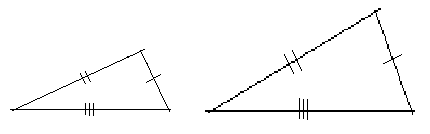
3. Forholdet mellom alle tre par koresponderende sider er det samme.
Forholdet mellom koresponderende sider i to fomlike trekanter er konstant. Dersom en trekant har siden A, B og C og en annen formlik trekant har koresponderende sider a, b og c er <tex> \quad \frac Aa = \frac Bb = \frac Cc = k</tex>