Sinusfunksjonen: Forskjell mellom sideversjoner
Fra Matematikk.net
Ny side: f (x)= sin x er definert for alle reelle tall. Verdimengden er [-1,1] Sinusfunksjonen er periodisk med 2pi. På figuren ser du hvordan funksjonen forskyves i koordinatsystemet. Tallene på ... |
Ingen redigeringsforklaring |
||
| Linje 1: | Linje 1: | ||
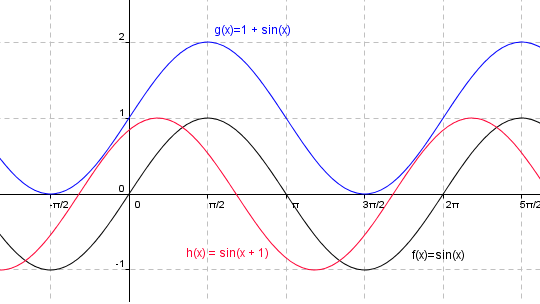
f (x)= sin x er definert for alle reelle tall. Verdimengden er [-1,1] Sinusfunksjonen er periodisk med 2pi. På figuren ser du hvordan funksjonen forskyves i koordinatsystemet. Tallene på x-aksen er radianer (absolutt vinkelmål).Ved å legge en konstant til sinusfunksjonen forskyves grafen loddrett. Ved å legge en konstant til vinkelen x forskyves grafen vannrett. | f (x)= sin x er definert for alle reelle tall. Verdimengden er [-1,1] Sinusfunksjonen er periodisk med 2pi. På figuren ser du hvordan funksjonen forskyves i koordinatsystemet. Tallene på x-aksen er radianer (absolutt vinkelmål).Ved å legge en konstant til sinusfunksjonen forskyves grafen loddrett. Ved å legge en konstant til vinkelen x forskyves grafen vannrett. | ||
[[Bilde:Sinfunk.png]] | |||
---- | ---- | ||
[[kategori:lex]] | [[kategori:lex]] | ||
Sideversjonen fra 1. aug. 2011 kl. 19:13
f (x)= sin x er definert for alle reelle tall. Verdimengden er [-1,1] Sinusfunksjonen er periodisk med 2pi. På figuren ser du hvordan funksjonen forskyves i koordinatsystemet. Tallene på x-aksen er radianer (absolutt vinkelmål).Ved å legge en konstant til sinusfunksjonen forskyves grafen loddrett. Ved å legge en konstant til vinkelen x forskyves grafen vannrett.