Løsning del 2 utrinn Vår 10: Forskjell mellom sideversjoner
m Teksterstatting – «<tex>» til «<math>» |
|||
| Linje 6: | Linje 6: | ||
Mobil + headset som koster 899kr + 598 kr = 1497kr<p></p> | Mobil + headset som koster 899kr + 598 kr = 1497kr<p></p> | ||
b) Utstyret koster egentlig 899kr + 249kr + 399kr + 249kr = 1766 kr<p></p> | b) Utstyret koster egentlig 899kr + 249kr + 399kr + 249kr = 1766 kr<p></p> | ||
Avslaget blir da 166kr. Rabatten i prosent blir < | Avslaget blir da 166kr. Rabatten i prosent blir <math> \frac{166}{1766}\cdot 100</tex >% = 9,4%<p></p> | ||
c) Her gjelder multiplikasjonsprinsippet. Det betyr at man ganger sammen antall valgmuligheter fra hver gruppe. To mobiler, tre vesker og to minnekort gir < | c) Her gjelder multiplikasjonsprinsippet. Det betyr at man ganger sammen antall valgmuligheter fra hver gruppe. To mobiler, tre vesker og to minnekort gir <math>2 \cdot 3 \cdot 2 =12</tex>mulige kombinasjoner.<p></p> | ||
d) Dersom begge skal kjøpe mobilvesker med feil må Maria trekke en med feil. Sannsynligheten for at det skjer er < | d) Dersom begge skal kjøpe mobilvesker med feil må Maria trekke en med feil. Sannsynligheten for at det skjer er <math> \frac{2}{15}</tex>.Så må Terese velge den andre med feil. Det er nå 14 vesker igjen, en med feil. Sannsynligheten for at Terese velger en feilvare er da <math> \frac{1}{14}</tex>. | ||
<p></p> | <p></p> | ||
Sannsynligheten for at begge velger feilvare blir da < | Sannsynligheten for at begge velger feilvare blir da <math>\frac{2}{15} \cdot \frac{1}{14} = \frac{1}{105}</tex>, eller 0.95%. | ||
== Oppgave 2 == | == Oppgave 2 == | ||
a) På min figur er diagonalen 3,9 cm lang. Siden målestokken er 1:2 betyr det at diagonalen i virkeligheten er 7,8 cm. | a) På min figur er diagonalen 3,9 cm lang. Siden målestokken er 1:2 betyr det at diagonalen i virkeligheten er 7,8 cm. | ||
<p></p> | <p></p> | ||
b) Omgjort til tommer blir det < | b) Omgjort til tommer blir det <math> \frac{7,8}{2,54}tommer = 3,1 tommer</tex> | ||
<p></p> | <p></p> | ||
c) Skjermen er kvadratisk. Diagonalen er 2,5 tommer = 6,35 cm.<p></p> | c) Skjermen er kvadratisk. Diagonalen er 2,5 tommer = 6,35 cm.<p></p> | ||
Pytagoras gir oss:<p></p> | Pytagoras gir oss:<p></p> | ||
< | <math>(6,35cm)^2 = x^2 + x^2 \\40,32cm^2 =2x^2 \\x^2 = 20,2cm^2 </tex><p></p> | ||
Arealet av skjermen er 20,2 kvadratcentimeter. | Arealet av skjermen er 20,2 kvadratcentimeter. | ||
| Linje 37: | Linje 37: | ||
250 min : kr 0,92 <p></p> | 250 min : kr 0,92 <p></p> | ||
350 min : kr 0,65 <p></p> | 350 min : kr 0,65 <p></p> | ||
f) Kostnad per ringeminutt er lik 229kr delt på antall ringeminutter. Dersom kostnaden per ringeminutt er y og antall ringeminutter x er sammenhengen: < | f) Kostnad per ringeminutt er lik 229kr delt på antall ringeminutter. Dersom kostnaden per ringeminutt er y og antall ringeminutter x er sammenhengen: <math>y = \frac {229}{x}</tex> Dersom y skal være 0,79 kroner løser man likningen:<p></p> | ||
< | <math>y = \frac {229}{x} \\ | ||
0,79 = \frac {229}{x} \\ | 0,79 = \frac {229}{x} \\ | ||
0,79x = 229 \\ | 0,79x = 229 \\ | ||
| Linje 50: | Linje 50: | ||
[[Bilde:4a2010.png]]<p></p> | [[Bilde:4a2010.png]]<p></p> | ||
b)<p></p> | b)<p></p> | ||
< | <math> Gjennomsnitt = \frac {254,5+220,9+208,3+204,7+205,4+223,2}{6}= 219,5</tex><p></p> | ||
c) <p></p>[[Bilde:4c2010.png]]<p></p> | c) <p></p>[[Bilde:4c2010.png]]<p></p> | ||
d) June vil spare på å bytte leverandør. Dersom hun mener hun hun vil ringe mere i fremtiden bør hun velge fastpris.<p></p> | d) June vil spare på å bytte leverandør. Dersom hun mener hun hun vil ringe mere i fremtiden bør hun velge fastpris.<p></p> | ||
| Linje 67: | Linje 67: | ||
b) <p></p> | b) <p></p> | ||
< | <math> \frac{x}{5,4cm}=1,618 \\ x = 8,7cm</tex> <p></p> | ||
Kredittkortet har en lengde på ca 8,7cm. | Kredittkortet har en lengde på ca 8,7cm. | ||
| Linje 84: | Linje 84: | ||
[[Bilde:7b2010.png]]<p></p> | [[Bilde:7b2010.png]]<p></p> | ||
Man bruker Pytagoras på trekanten EBC. Man vet at EB = 1 og BC = 2. Da blir < | Man bruker Pytagoras på trekanten EBC. Man vet at EB = 1 og BC = 2. Da blir <math> EC = \sqrt{5}</tex>. Det betyr også at lengden <math> EF = \sqrt{5}</tex>. | ||
<p></p> | <p></p> | ||
Man får: < | Man får: <math> \frac{AF}{AD} = \frac{AE + EF}{AD} = \frac {1 + \sqrt{5}}{2}</tex><p> | ||
Hvilket skulle vises. | Hvilket skulle vises. | ||
Sideversjonen fra 5. feb. 2013 kl. 20:57
Oppgave 1
a) Hun kan kjøpe mobil + minnekort + handsfree som koster
899kr + 249kr + 399kr = 1547kr eller
Mobil + headset som koster 899kr + 598 kr = 1497kr
b) Utstyret koster egentlig 899kr + 249kr + 399kr + 249kr = 1766 kr
Avslaget blir da 166kr. Rabatten i prosent blir <math> \frac{166}{1766}\cdot 100</tex >% = 9,4%
c) Her gjelder multiplikasjonsprinsippet. Det betyr at man ganger sammen antall valgmuligheter fra hver gruppe. To mobiler, tre vesker og to minnekort gir <math>2 \cdot 3 \cdot 2 =12</tex>mulige kombinasjoner.
d) Dersom begge skal kjøpe mobilvesker med feil må Maria trekke en med feil. Sannsynligheten for at det skjer er <math> \frac{2}{15}</tex>.Så må Terese velge den andre med feil. Det er nå 14 vesker igjen, en med feil. Sannsynligheten for at Terese velger en feilvare er da <math> \frac{1}{14}</tex>.
Sannsynligheten for at begge velger feilvare blir da <math>\frac{2}{15} \cdot \frac{1}{14} = \frac{1}{105}</tex>, eller 0.95%.
Oppgave 2
a) På min figur er diagonalen 3,9 cm lang. Siden målestokken er 1:2 betyr det at diagonalen i virkeligheten er 7,8 cm.
b) Omgjort til tommer blir det <math> \frac{7,8}{2,54}tommer = 3,1 tommer</tex>
c) Skjermen er kvadratisk. Diagonalen er 2,5 tommer = 6,35 cm.
Pytagoras gir oss:
<math>(6,35cm)^2 = x^2 + x^2 \\40,32cm^2 =2x^2 \\x^2 = 20,2cm^2 </tex>
Arealet av skjermen er 20,2 kvadratcentimeter.
Oppgave 3
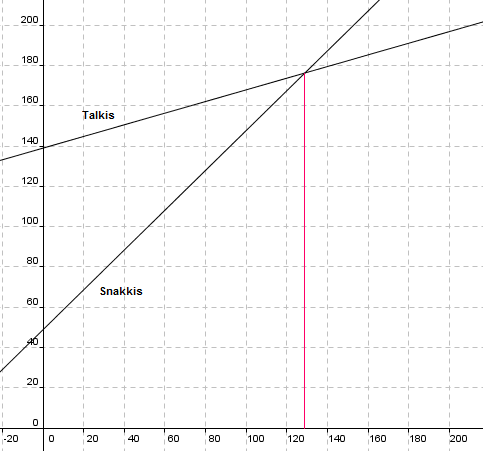
a) Han har "Snakkis"
b)
1) Det koster 0,99 kr per minutt, og x er antall ringeminutter. Kostnaden blir da 0,99 ganger x pluss fastprisen som er kr 49.
2) y = 0,29x + 139
c)
d) Ut fra grafene ser man at Snakkis er billigst opp til 129 ringeminutter. Talkis er billigst over 129 ringeminutter.
e) Tallene som mangler i tabellen er;
50 min: kr 4,58
150 min : kr 1,53
250 min : kr 0,92
350 min : kr 0,65
f) Kostnad per ringeminutt er lik 229kr delt på antall ringeminutter. Dersom kostnaden per ringeminutt er y og antall ringeminutter x er sammenhengen: <math>y = \frac {229}{x}</tex> Dersom y skal være 0,79 kroner løser man likningen:
<math>y = \frac {229}{x} \\ 0,79 = \frac {229}{x} \\ 0,79x = 229 \\ x= \frac{229}{0,79}
x=290 </tex>
Hun må ringe 290 minutter for at kostnaden per ringeminutt skal bli 0,79 kr.
Oppgave 4
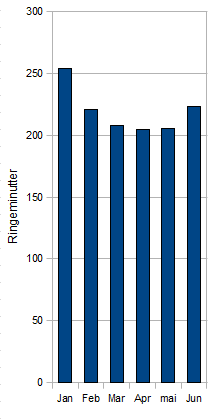
a)
b)
<math> Gjennomsnitt = \frac {254,5+220,9+208,3+204,7+205,4+223,2}{6}= 219,5</tex>
c)
d) June vil spare på å bytte leverandør. Dersom hun mener hun hun vil ringe mere i fremtiden bør hun velge fastpris.
Hanna bør også vurdere å bytte abonnement, med mindre hun har plane om å ringe mye mer i fremtiden enn det hun gjør nå.
Oppgave 5
a)
Nano: 2,9cm (B) x 3,8cm (H), 3,8:2,9=1,31
Classic: 3,4cm x 5,7cm, 5,7:3,4 = 1,676
Touch: 3,4cm x 6,1 cm, 6,1:3,4 = 1,79
Classic har en form som ligg nært opp til et gyllent rektangel.
b)
<math> \frac{x}{5,4cm}=1,618 \\ x = 8,7cm</tex>
Kredittkortet har en lengde på ca 8,7cm.
Oppgave 6
a) De neste tallene er 5 + 8 = 13 og 8 + 13 = 21. Et tall i følgen er summen av de to tallene foran.
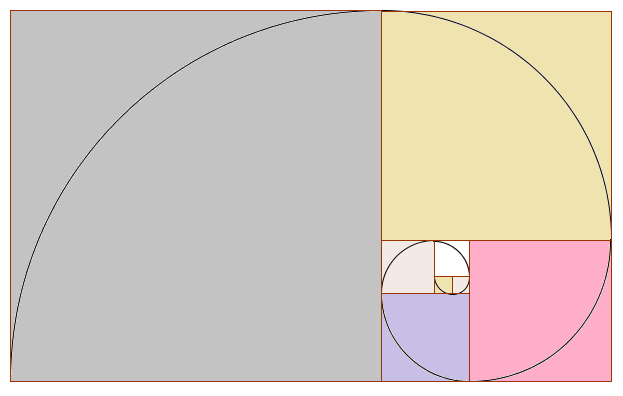
b og c)
Med kvadrat 7 og 8 ser det slik ut:
d) Ved å prøve seg fram ser man at 55 delt på 34 er de minste verdiene som gir ønsket nøyaktighet. Man må altså ha med 10 kvadrater.
Oppgave 7
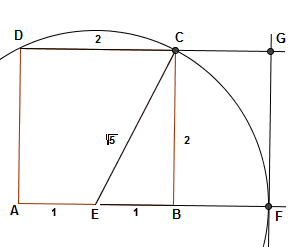
a) Følg oppskriften gitt i oppgaven, samt hjelpefigur.
b)
Man bruker Pytagoras på trekanten EBC. Man vet at EB = 1 og BC = 2. Da blir <math> EC = \sqrt{5}</tex>. Det betyr også at lengden <math> EF = \sqrt{5}</tex>.
Man får: <math> \frac{AF}{AD} = \frac{AE + EF}{AD} = \frac {1 + \sqrt{5}}{2}</tex>
Hvilket skulle vises.