S1 2024 Høst LØSNING: Forskjell mellom sideversjoner
| Linje 112: | Linje 112: | ||
=====c)===== | =====c)===== | ||
Påstanden er feil for | |||
a= - 1 gir løsninger når både x og y er partall, eller når begge er oddetall | |||
====Oppgave 3==== | ====Oppgave 3==== | ||
Sideversjonen fra 19. des. 2024 kl. 06:26
Diskusjon av oppgaven på matteprat
DEL EN
Oppgave 1
Deriverer f:
Oppgave 2
Programmet leter etter toppunktet til funksjonen
Programmet løper gjennom en while løkke og sjekker funksjonsverdien O(x+1) i forhold til O(x). Så lenge O(x+1)> O(x) fortsetter løkken. Når det ikke lenger er tilfellet, skriver det ut x- verdien.
Vi deriver O og setter uttrykket lik null.
Programmet skriver ut 10000, som er x verdien som gir størst funksjonsverdi.
Oppgave 3
Vi er bare interessert i den positive verdien fordi vi ikke kan opphøye 10 i noe som gir en negativ verdi.
Oppgave 4
Oppgave 5
a)
To kuler med samme farge:
P(to i samme farge) = P(to røde) + P(to blå) + P( to gule)
b)
Nøyaktig en gul
Oppgave 6
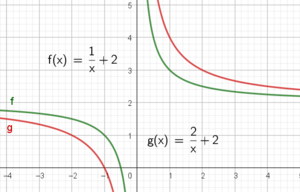
Både g og f tilfredsstiller kravet om gjennomsnittlig vekstfart i intervallet [0,4]. g har derivert lik 0,5 for alle x, så det er kun f som tilfredsstiller kravene.
DEL TO
Oppgave 1
a)
Forskjellige antrekk (multiplikasjonsprinsippet):
FA =
b)
c)
Oppgave 2
a)
Gjennomsnittlig vekstfart:
Påstanden er riktig.
b)
Begge går mot samme grenseverdi når x går mot pluss eller minus uendelig. Påstanden er feil.
c)
Påstanden er feil for
a= - 1 gir løsninger når både x og y er partall, eller når begge er oddetall
Oppgave 3
Logaritmen til basisen for logaritmen er 1. Eksempelvis er
Oppgave 4
Oppgave 5
a)
Antall parkeringsplasser nå er x
Inntekter nå er 1000x per måned
Dersom prisen øker med 500 kr. vil hun miste 10 kunder, men leieinntektene forblir de samme:
b)
Antall utleide plasser:
Inntekt:
Finner hvilken pris som gir maksimal inntekt ved å sette den deriverte av inntektsfunksjonen lik null:
Den maksimale inntekten blir da:
Den månedlige maksimalinntekten er på 31250 kr.
Oppgave 6
a)
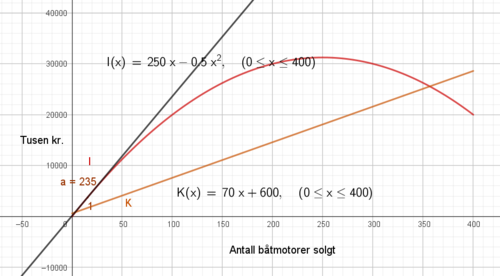
Den deriverte av I når x er 15 gir oss inntektsendringen ved salg av enhet 15. Man øker inntekten med 235 000 kroner ved salg av motor nr. 15.
b)
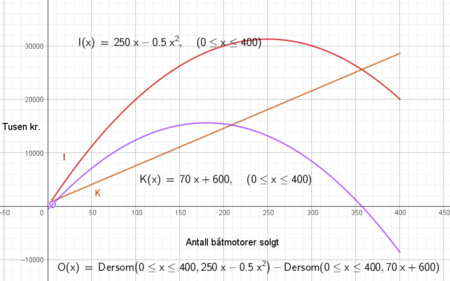
Overskuddet er størst når det selges 180 enheter. Da er overskuddet 15 600 000kr.
c)
Oppgave 7
Sannsynlighet for positiv test:
Sannsynligheten for at personen er smittet gitt positiv test er litt i overkant av 33%
Selv om testen har høy sensitivitet (99%) og spesifisitet (98%), fører den lave grunnsannsynligheten for å være smittet (P(S)=1%) til at sannsynligheten for å være smittet selv etter en positiv test fortsatt er relativt lav. Dette er et eksempel på hvordan grunnsannsynligheten påvirker tolkningen av testresultater, en problemstilling som ofte oppstår i medisinsk diagnostikk.