S1 2024 Høst LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

DEL EN

Oppgave 1

$f(x) = \frac{e^{2x}}{x}$

Deriverer f: $f'(x) = \frac{(e^{2x})' \cdot x + x' \cdot e^{2x}}{x^2} = \frac{2xe^{2x} + e^{2x}}{x^2} = \frac{e^{2x} (2x + 1)}{x^2} $

Oppgave 2

Programmet leter etter toppunktet til funksjonen $O(x) = -0,1x^2+2000x-50000$.

Programmet løper gjennom en while løkke og sjekker funksjonsverdien O(x+1) i forhold til O(x). Så lenge O(x+1)> O(x) fortsetter løkken. Når det ikke lenger er tilfellet, skriver det ut x- verdien.

Vi deriver O og setter uttrykket lik null.

$-0,2x + 2000 =0$

$x = \frac{-2000}{-0,2} = 10000 $

Programmet skriver ut 10000, som er x verdien som gir størst funksjonsverdi.

Oppgave 3

$100 ^x - 3 \cdot 10^x= 4$

$ (10^2)^x - 3 \cdot 10^x-4 =0$

$(10^x)^2 - 3 \cdot 10^x- 4 = 0$

$10^x = \frac{3 \pm \sqrt{9+16}}{2}$

$10^x = \frac{3 \pm 5}{2}$

Vi er bare interessert i den positive verdien fordi vi ikke kan opphøye 10 i noe som gir en negativ verdi.

$10^x = 4$

$x = lg(4)$

Oppgave 4

\[ \lim_{x\to \infty} \frac{x^2+x-12}{2x^2 -18} \]

\[ \lim_{x\to \infty} \frac{\frac{x^2}{x^2}+ \frac{x}{x^2}- \frac{12}{x^2}}{ \frac{2x^2}{x^2} - \frac{18}{x^2}} \]

\[ \lim_{x\to \infty} \frac{1 + \frac{1}{x}- \frac{12}{x^2}}{ 2 - \frac{18}{x^2}} = \frac 12 \]

Oppgave 5

a)

To kuler med samme farge:

P(to i samme farge) = P(to røde) + P(to blå) + P( to gule)

$ \frac {4} {9} \cdot \frac {3} {8} + \frac {3} {9} \cdot \frac {2} {8} +\frac {2} {9} \cdot \frac {1} {8} = \frac {12+6+2} {72} = \frac {5} {18} $

b)

Nøyaktig en gul

$ P(en gul) = P(gul) \cdot P(annen farge) + P(annen farge) \cdot P( gul) $

$ P(en gul)= \frac {2} {9} \cdot \frac {7} {8} + \frac {7} {9 } \cdot \frac {2} {8} = \frac {28} {72} = \frac {7} {18} $

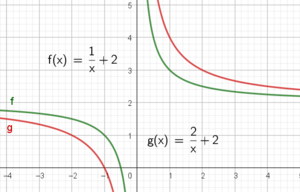
Oppgave 6

Både g og f tilfredsstiller kravet om gjennomsnittlig vekstfart i intervallet [0,4]. g har derivert lik 0,5 for alle x, så det er kun f som tilfredsstiller kravene.

DEL TO

Oppgave 1

a)

Forskjellige antrekk (multiplikasjonsprinsippet):

FA = $10 \cdot 20 \cdot 15 \cdot 15 \cdot 5= 225 000 $

Oppgave 2

a)

Gjennomsnittlig vekstfart: $\frac {\Delta y}{\Delta x} = \frac{f(4) - f(1) }{4-1} = \frac{18-3}{3} = 5$

Påstanden er riktig.

b)

Begge går mot samme grenseverdi når x går mot pluss eller minus uendelig. Påstanden er feil.

c)

Dersom to like grunntall skal være like når de er opphøyet i en eller annen eksponent, må også eksponentene være like. Påstanden er riktig.

Oppgave 3

Logaritmen til basisen for logaritmen er 1. Derfor er basis her 5.

Oppgave 6