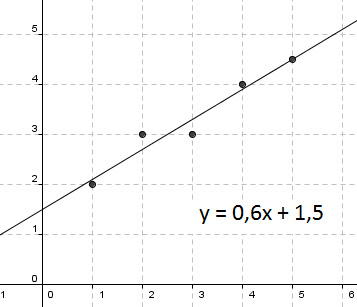Regresjon: Forskjell mellom sideversjoner
| Linje 210: | Linje 210: | ||
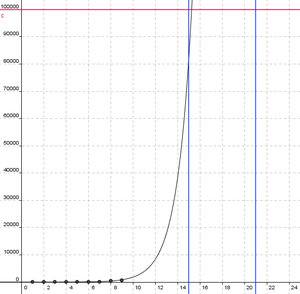
Man observerer at funksjonen <tex>f(x)=0,88\cdot 2,14^x</tex> stiger raskt. I uke 21 vil det være <tex>f(21)=0,88\cdot 2,14^{21} = 8000000</tex>. I slutten av forplantningssessongen kan det være ca 8 millioner insekter. Grafen i høyremargen viser utviklingen til ca 100000 insekter. | Man observerer at funksjonen <tex>f(x)=0,88\cdot 2,14^x</tex> stiger raskt. I uke 21 vil det være <tex>f(21)=0,88\cdot 2,14^{21} = 8000000</tex>. I slutten av forplantningssessongen kan det være ca 8 millioner insekter. Grafen i høyremargen viser utviklingen til ca 100000 insekter. | ||
I uke 15 eller 16 vil 100000 innsekter passeres. Det betyr at myndighetene kun har 6-7 uker (fra siste måling) til å ordne opp i problemet. Rådet må altså være . Sett i gang | I uke 15 eller 16 vil 100000 innsekter passeres. Det betyr at myndighetene kun har 6-7 uker (fra siste måling) til å ordne opp i problemet. Rådet må altså være . Sett i gang tiltak snarest!! | ||
Sideversjonen fra 22. des. 2010 kl. 09:31
Innledning
Poenget med regresjon er at man ut fra noen få målinger (observasjoner) lager en matematisk funksjon som forutsier hendelsen innenfor et visst område.
Så langt har vi tegnet grafer ut fra kjente funksjonsuttrykk. I mange fag som økonomi, teknikk og naturfagene, er det ofte ønskelig å finne en sammenheng mellom forskjellige størrelser.
Man kan måle og observere sammenhengen mellom størrelse og på det grunnlag formulere et funksjonsuttrykk som gir en sammenheng.
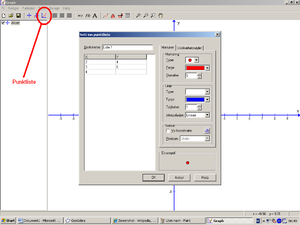
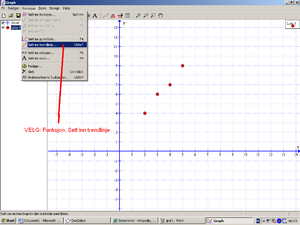
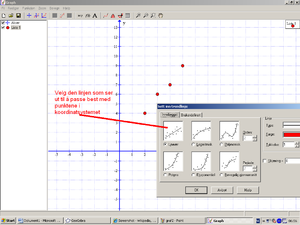
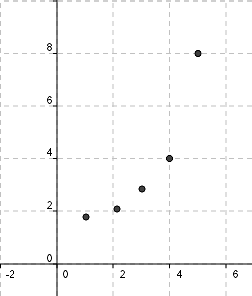
Over ser man forskjellige grafer som representerer matematiske funksjoner. Modelleringen består i hovedsak å finne en matematisk funksjon som passer til de måledata man har og finne ut i hvilket område modellen har gyldighet. Man har følgende data plottet i et koordinatsystem:
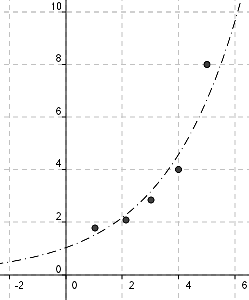
Oppgaven blir å finne en kurve / graf som passer best mulig til målepunktene. Man ser at graf nr. 2 over trolig er den som passer best. For å finne grafen og det matematiske uttrykket bruker vi digitale hjelpemidler. Det finnes mange digitale hjelpemiddler du kan bruke, inkludert kalkulator. Hovedsaken er at du lærer deg å bruke hjelpemiddlet godt.
Man observerer at grafen ikke helt passer til målepunktene, men den passer ganske godt. Hvor godt den passer er r et mål på.
Koeffisienten r
Når vi benytter regresjon går vi fra noen målepunkter (sammenhørende x og y verdier) til en generell sammenheng mellom x og y, uttrykt ved et funksjonsuttrykk.
Et mål på hvor god vår modell er finner vi ved å se på bestemmelseskoeffisienten r. Verdiene for r varierer mellom -1 og 1, avhengig av hvor god tilpassningen er mellom data og trendlinje (graf) er. Dersom r er nær 0 er tilpassningen dårlig. Desto nærmer 1 eller -1 r- verdien kommer, desto bedre tilpassning.
Vi velger altså den regresjonstypen med r verdi lengst fra null (nær 1 eller -1). Dersom man ser på <tex>r^2</tex> skal den være så nær en som mulig for å representere en god modell.
Når man lager modeller på denne måten må man tenke på området modellen er gyldig i. Dersom man lager en modell i Mai, for veksten av en blomst, vil modellen ha et gyldighetsområde. Det kan være fra Mai til oktober. Det er lite trolig at modellen er gyldig i Desember, når det er mørkt, kaldt og snøen liggger i hagen.
Lineær regresjon
Figur 1 viser en rett linje. Dersom man har målepunker som ligger nesten på linje er det mulig at lineær regresjon er den beste modellen.
Man vil da få en funksjon av typen:
f(x) = ax+b
Dersom man har har følgende observasjoner
| x - verdi | 1 | 2 | 3 | 4 | 5 |
| y - verdi | 2 | 3 | 3 | 4 | 4,5 |
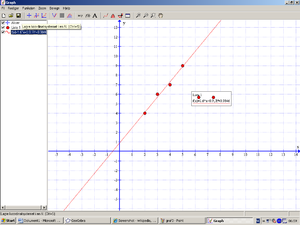
Plotter man disse i et koordinatsystem får man:
Dataprogrammet gir oss funksjonsyttrykket til den linjen som passer best med måledataene. I dette tilfellet er det
y=0,6x+1,5
<tex>r^2 = 0,95</tex> noe som tyder på at dette er en akseptabel modell.
Dersom man regner med at modellen er gyldig i området fra 0 til 20 x kan man bruke den til å regne ut verdier for y for større x-verdier enn 5, som var den høyeste x verdi i målingene.
Dersom man lurer på hva y er når x er 15,er det bare å sette inn 15 for x i funksjonsuttrykket:
<tex>y = 0,6 \cdot 15 + 1,5 = 10,5</tex>
På denne måten kan man "forutsi" hva y blir for andre x-verdier enn de vi har målt.
Eksponentiell regresjon
Dersom noe øker sakte til å begynne med, for så å øke rakt, som i figur 2, kan man trolig bruke en eksponentiell modell.
Det samme gjelder dersom noe avtar raskt, for så nesten å flate ut, som i figur 3.
En eksponentiell funksjon er på formen <tex>f(x)=a \cdot b^x </tex>
Dersom grunntallet b er større enn en vokser funksjonen som i figur 2. Dersom b er mindre enn en avtar funksjonen med økende x verdier, som i figur 3.
Desom man har følgende observasjoner:
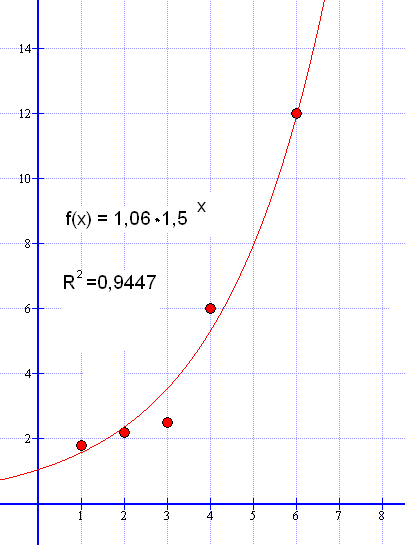
| x - verdi | 1 | 2 | 3 | 4 | 5 |
| y - verdi | 1,8 | 2,2 | 2,5 | 6 | 12 |
kan man plotte punktene i et koordinatsystem. Om man velger en trendlinje som er eksponentiell får man følgende kurve:
<tex>F(x) = 1,06 \cdot 1,5^x</tex>
Man observerer at grunntallet er 1,5 , altså større enn en, og det betyr at grafen vokser mot høyre. Figuren er laget i Graph som kan lastes ned her:[1]
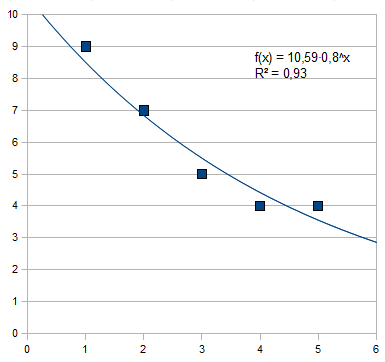
| x - verdi | 1 | 2 | 3 | 4 | 5 |
| y - verdi | 9 | 7 | 5 | 4 | 4 |
<tex>f(x)=10,59 \cdot 0,8^x</tex>
Man observerer at grrunntallet er 0,8, altså mindere enn en, det betyr at grafen avtar mot høyre, altså når x blir større.
Figuren er laget i
http://no.openoffice.org/ regneark, Openoffice] som kan lastes ned gratis.
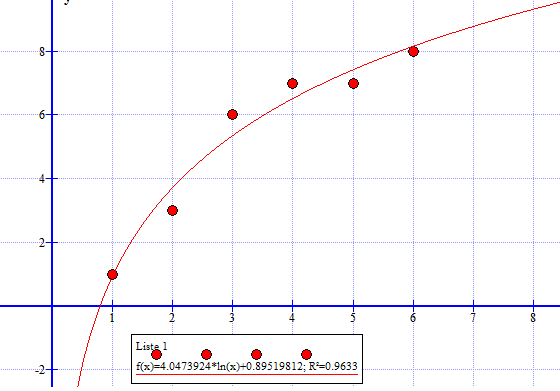
Logaritmisk regresjon
| x - verdi | 1 | 2 | 3 | 4 | 5 | 6 |
| y - verdi | 1 | 3 | 6 | 7 | 7 | 8 |
Polynom regresjon
Vi måler temperaturen kl. 13:00, 14:00, 15:00, 16:00, 18:00 og 20:00. Tidspunkt og temperatur plottes i et koordinatsystem. Hva blir temperaturen kl 22:00?
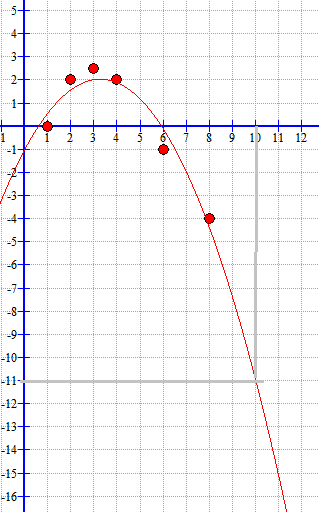
| x - verdi | 1 | 2 | 3 | 4 | 6 | 8 |
| y - verdi | 0 | 2 | 3 | 2 | -1 | -4 |
Her brukes polynomregresjon av andre grad, da blir funksjonen en parabel.
Fra figuren ser man at temperaturen vil bli ca. -11 grader, dersom modellen er gyldig. Husk at dette er en modell med en grad av usikkerhet, det er derfor meningsløst å oppgi desimaler. Funksjonsuttrykket for modellen er
<tex>f(x)= - 0,29x^2 + 1,89x - 1,06</tex>
<tex>r^2= 0,95</tex>
Innsatt for 10 i funksjonsyttrykket får man:
<tex>f(10)= - 0,29(10)^2 + 1,89\cdot10 - 1,06= -29 + 18,9 -1,06 =-11</tex>
Case
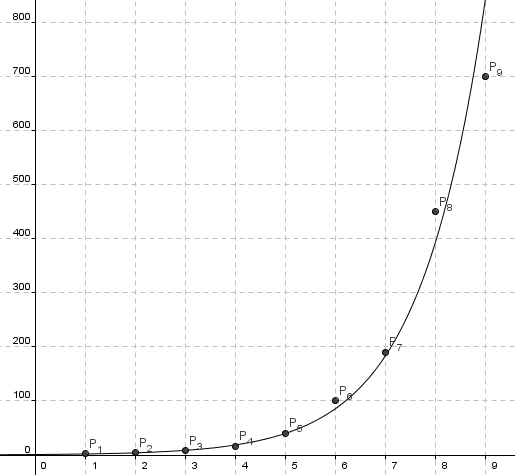
Du arbeider som biolog og får en melding om at et nytt ukjent insekt har blitt observert i en park nær deg!! Det er grunn til å tro at insektet kan skape ubalanse i parken ved at det spiser opp produsenter som er nyttige i næringskjeden. Du får ni uker på deg før myndighetene vil ha et råd fra deg. Du bestemmer deg for å få en oversikt over formeringsevnen ved å setter opp elektroniske telleapparater som avleses hver uke. Du foretar 9 avlesninger, en hver uke. Resultater:
| Uke nr. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Antall | 2 | 4 | 8 | 16 | 40 | 100 | 190 | 450 | 700 |
Erfaringer disse ukene vier at insektene ikke gjør så stor skade som først antatt og myndighetene vil ikke sette i gang tiltak før antallet innsekter eventuelt overskrider 100.000. Det er 12 uker igjen av forplantningssesongen. Hva blir ditt råd til myndighetene?
Man observerer at funksjonen <tex>f(x)=0,88\cdot 2,14^x</tex> stiger raskt. I uke 21 vil det være <tex>f(21)=0,88\cdot 2,14^{21} = 8000000</tex>. I slutten av forplantningssessongen kan det være ca 8 millioner insekter. Grafen i høyremargen viser utviklingen til ca 100000 insekter. I uke 15 eller 16 vil 100000 innsekter passeres. Det betyr at myndighetene kun har 6-7 uker (fra siste måling) til å ordne opp i problemet. Rådet må altså være . Sett i gang tiltak snarest!!