1P 2024 vår LK20 LØSNING

Oppgaven som pdf

Løsningsforslag

Diskusjon av oppgaven på matteprat

DEL 1

Oppgave 1

18 millioner mennesker tilsvarer 2 promille av verdens befolkning.

9 millioner mennesker tilsvarer 1 promille (tusendel) av verdens befolkning.

$9\,000\,000 \cdot 1000 = 9\,000\,000\,000 $

Hele verdens befolkning vil være på 9 milliarder mennesker på det tidspunktet.

Oppgave 2

a)

Tallet 20 000 er hvor mange kroner Ada setter på sparekonto. Tallet 1,0485 er vekstfaktoren for en årlig rente på 4,85 %.

b)

Tallet som blir skrevet ut forteller hvor mange kroner sparebeløpet gjennomsnittlig øker med per år, fra 0 til 10 år.

Oppgave 3

Grafen til f viser sammenhengen mellom to størrelser som er proporsjonale. Dette er fordi grafen til f går gjennom origo, og øker med et konstant stigningstall på 125. Vi kan skrive funksjonsuttrykket til f på formen y = kx, der k er konstant. I dette tilfellet har vi y=125x.

Grafen til p viser sammenhengen mellom to størrelser som er omvendt proporsjonale. Vi kan skrive funksjonsuttrykket til p på formen y = k/x, der k er konstant. For eksempel er y=1000 når x=1, mens y=500 når x=2. Vi har funksjonen y=1000/x.

Oppgave 4

a)

Vi bruker formelen som er gitt i oppgaven. Farten delt på 10 er 7, så vi setter derfor inn 7 for x i formelen.

$B=\frac{x^2}{2}$

$B=\frac{7^2}{2}=\frac{49}{2}=24,5$

Slik kan Viking Redningstjeneste ha regnet ut bremselengden.

b)

Vi skal finne x, så vi gjør om formelen først slik at den er uttrykt ved x.

$B=\frac{x^2}{2}$

$x^2=B\cdot 2$

$x=\sqrt{2B}$

Vi setter inn 40,5 meter for B i formelen og regner ut x:

$x=\sqrt{2\cdot 40,5}=\sqrt{81}=9$

x = 9, det vil si at farten til bilen er 90 km/h.

DEL 2

Oppgave 1

a)

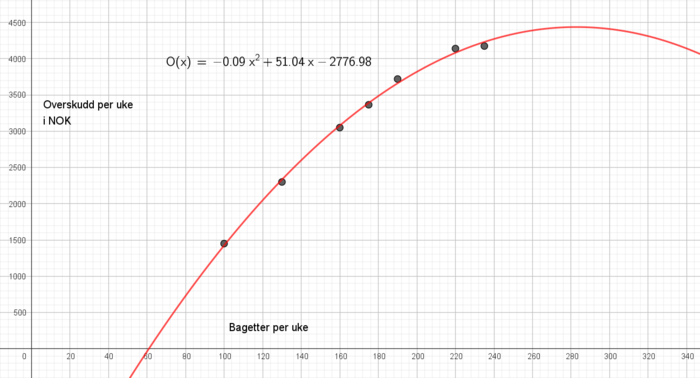
Vi bruker regresjon i Geogebra og får:

b)

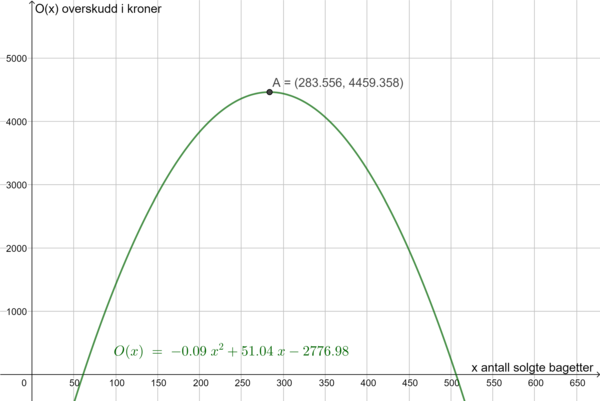
Vi bruker modellen fra oppgave a og finner ekstremalpunktet (i dette tilfellet toppunktet) i Geogebra.

Kantina må produsere omtrent 284 bagetter og vil da få omtrent 4460 kr i overskudd. Merk at en modell ikke gir noe nøyaktig svar, men vi kan anslå omtrent hvor mange bagetter kantina burde selge og hva overskuddet blir.

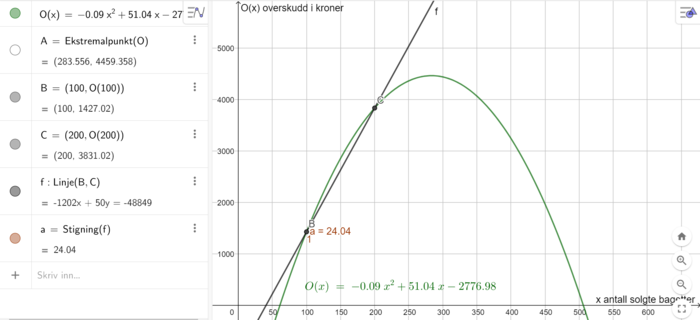
c)

Linjen f har stigningstall på ca. 24. Det betyr at overskuddet øker i gjennomsnitt 24 kroner per bagett, når bagettsalget økes med én, for salg mellom 100 og 200 bagetter.

Oppgave 2

a)

Ved regning:

$105\,607\cdot 1,0325^5=123\,920$

Det vil være 123 920 kr på konto om fem år.

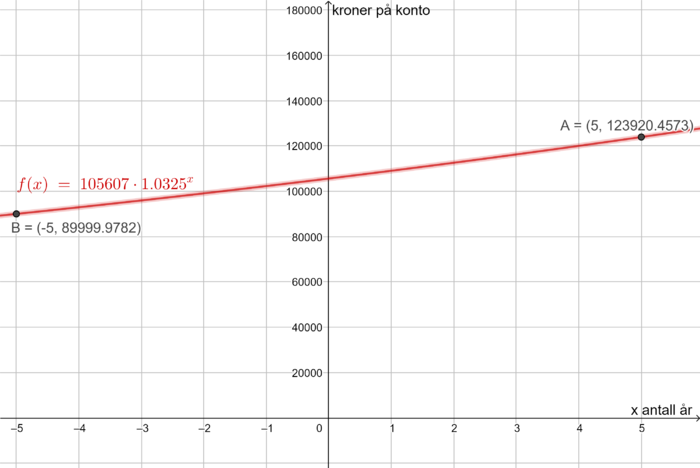
Grafisk: samme svar, se punkt A på skjermutklippet fra Geogebra.

b)

Ved regning:

$105\,607\cdot 1,0325^{-5}=90\,000$

Det var 90 000 kr på konto for fem år siden.

Grafisk: samme svar, se punkt B på skjermutklippet fra Geogebra.

Oppgave 3

1 fat = 158,987 liter

a)

$1\,794\,000 \cdot 158,987 \cdot 365 = 104\,106\,277\,470 \approx 1,04\cdot 10^{11}$

Det ble produsert omtrent $1,04\cdot 10^{11}$ liter olje på norsk sokkel i 2023.

b)

$\frac{1,794-1,685}{1,685}\cdot 100 = 6,47$

Produksjonsmengden steg med 6,47 % fra 2022 til 2023.

Oppgave 4

a)

Det tok 1500 m / 400 m per runde = 3,75 runder å løpe 1500 m på denne banen.

3 min = 180 sekunder.

Jakob brukte 180 s + 27,14 s = 207,14 sekunder på 1500 m.

Jakob brukte gjennomsnittlig 207,14 s / 3,75 runder = 55,24 sekunder per runde.

b)

Basert på de andre tidene vil jeg si at det er mellom 1500 m og 2000 m i en engelsk mil.

Regner om km/h til m/s:

$\frac{25,89\cdot 1000}{3600} = 7,19$ m/s

Jakob løp den engelske mila med en fart på 7,19 m/s. Han løp med en tid på 3:43,73, som tilsvarer 180 + 43,73 = 223,73 sekunder.

For å finne strekningen, ganger vi farten med tiden:

$7,19m/s \cdot 223,73s = 1608,6$ m

Det er omtrent 1609 meter i en engelsk mil.

Oppgave 5

2 + 3 = 5

5 + 6 = 11

11 + 12 = 23

23 + 24 = 47

n + (n+1) = neste tall

Mønsteret går ut på å legge til neste heltall, til det tallet man allerede har. For et tall n, legger man til n+1, slik at neste tall blir n + n + 1. Dette kan skrives som 2n + 1, og vil alltid være et oddetall, fordi man har to-gangen (et partall) pluss én. Tar man et partall og legger til én, vil man alltid få et oddetall.

Oppgave 6

a)

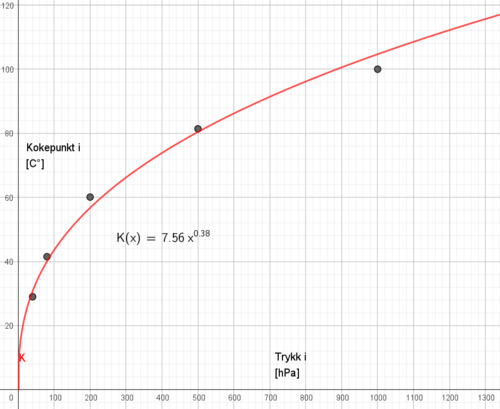
Bruker potensregresjon og får modellen $K(x)=7,56x^{0,38}$

b)

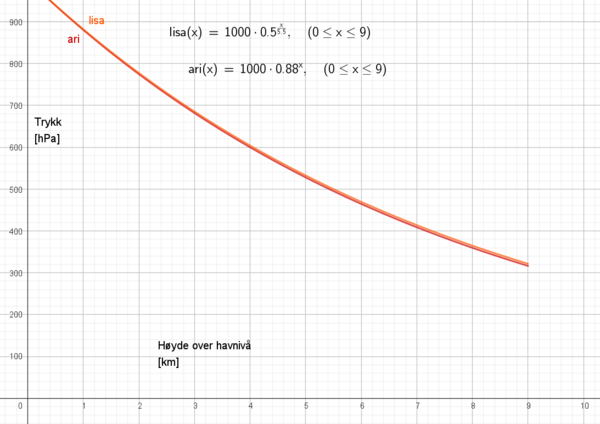
Bruker en eksponentiell modell for Ari: $ari(x)=1000\cdot 0,88^x$

Bruker en annen eksponentiell modell for Lisa: $lisa(x)=1000\cdot 0,5^{x/5,5}$

Det er ingen fjell høyere enn 9 km, derfor går definisjonsmengden fra null til ni. Vi observerer at modellene er ganske like, så hvilken vi bruker har liten betydning.

c)

Dersom man skal få hardkokte egg må temperaturen (kokepunktet) være over 85 grader, som tilsvarer et trykk på over 600hPa (Figur oppgave a).

Fra figuren i oppgave b ser man at trykket blir lavere enn 600 hPa når høyden overstiger ca. 4000 meter. Man bør holde seg på fjell under 4000 meter dersom man er avhengig av hardkokte egg. Alternativt kan man koke dem på forhånd og ta med på tur :-)

Oppgave 7

Til sammen kostet alle skoene i utgangspunktet: $800 + 1550 + 1350 = 3700$ kr.

Vennen sine sko utgjorde $\frac{1350}{3700}\cdot 100 = 37$ % av den opprinnelige prisen. Han burde derfor betale 37 % av prisen etter tilbudet.

Med tilbudet blir de billigste skoene gratis, så pris etter tilbud er $1350 + 1550 = 2900$ kr.

Vennen bør betale $0,37\cdot 2900 = 1073$ kr.

Du bør betale $2900 - 1073 = 1827$ kr.