Løsning del 1 utrinn Vår 23: Forskjell mellom sideversjoner
| Linje 61: | Linje 61: | ||
====a)==== | ====a)==== | ||
[[File:28052023-02.png| 300px]] | [[File:28052023-02.png| 300px]] | ||
Typetall er 62 (flest like verdier) | |||
Median er | |||
====b)==== | ====b)==== | ||
Sideversjonen fra 28. mai 2023 kl. 05:42
Diskusjon av denne oppgaven på matteprat
DEL EN
Oppgave 1
To likninger med to ukjente.
x = pris sjokolade og y = pris slikkepinne.
Bilde 1 gir:
2y + 2x =32 (deler alle ledd på 2 og flytter trekker fra x på begge sider)
y = 16 - x
Bilde 2 gir:
4y + 2x = 44 (setter inn for y)
4(16-x) +2x = 44 64 -2x = 44 x=10 Da blir y = 16 - 10 =6
Sjokoladen koster 10 kroner og slikkepinnen koster 6 kroner.
Alternativt kan man tenke: Forskjellen på bildene er to slikkepinner og 12 kroner, da må en slikkepinne koste 6 kroner (som er det eneste de spør om).
Oppgave 2
a)
b)
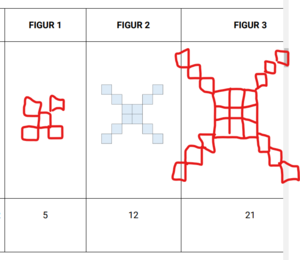
Dersom vi kaller figurnummeret for n: Kvadratet i midten består av $n^2$ småkvadrater. Så er det fire armer med n kvadrater.
Formelen blir da $B(n)= n^2 + 4n$
Oppgave 3
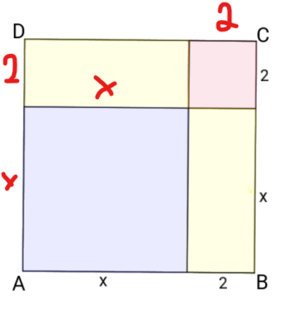
Ett gult felt har areal 2x. To gule felt har areal 4x.
Rosa kvadrat har areal 4.
Lilla kvadrat har areal $x^2$
Arealet av det store kvadratet med sidekanter (x+2) blir:
$(x+2)(x+2)= x^2+ 4x + 4$, som er det samme om vi legger sammen arealene av de fire små figurene. Dette er første kvadratsetning.
Oppgave 4
a)
Typetall er 62 (flest like verdier)
Median er