S1 2022 Vår LK20 LØSNING: Forskjell mellom sideversjoner
| Linje 103: | Linje 103: | ||
=DEL 2= | =DEL 2= | ||
[[File: S1-V22-del2-1.png]] | ==Oppgave 1== | ||
[[File: S1-V22-del2-1.png|800px]] | |||
===a)=== | |||
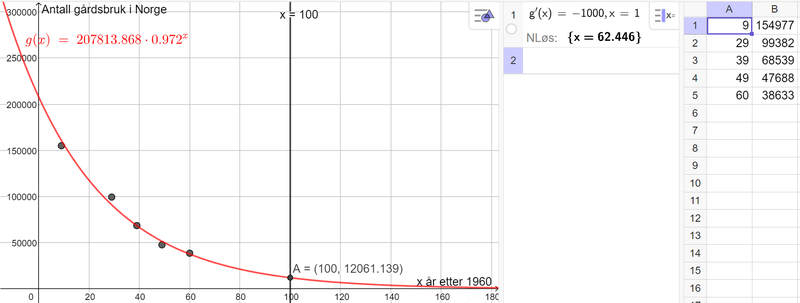
Velger å la x-verdiene være antall år etter 1960, og bruker regresjonsanalyse i Geogebra. | |||
==Oppgave | Velger en eksponentiell modell, da denne passer godt til dataene vi har. I tillegg er det usannsynlig at antall gårdsbruk i Norge blir null, så en eksponentiell modell hvor antall gårdsbruk fortsetter å avta uten å bli null, passer godt. | ||
Modellen er $g(x)=207814\cdot 0,972^x$ | |||
===b)=== | |||
Skriver x=100 i Geogebra (tilsvarer 100 år etter 1960, altså 2060) og finner skjæringspunktet mellom x=100 og grafen til g. Se punkt A=(100,12061). Ifølge modellen min vil det være 12061 gårdsbruk i Norge i 2060. | |||
===c)=== | |||
Bruker CAS i Geogebra og løser likningen $g'(x)=-1000$. CAS regner ut at $x=62,4$. Det vil si at ifølge modellen min, vil antall gårdsbruk i Norge avta med ca. 1000, ca. 62 år etter 1960, altså i år 2022. | |||
==Oppgave 2== | |||
Sideversjonen fra 28. des. 2022 kl. 14:20
Diskusjon av oppgaven på matteprat
Løsningsforslag laget av Farhan Omar
DEL 1
Oppgave 1
$(2a)^{-1}\cdot (\frac{b}{2})^{-3}\cdot(a\cdot b)^3$
$=2^{-1}\cdot a^{-1}\cdot b^{-3}\cdot 2^3\cdot a^3 \cdot b^3$
$=2^{-1+3}\cdot a^{-1+3} \cdot b^{-3+3}$
$=2^2\cdot a^2 \cdot b^0$
$=4a^2$
Oppgave 2
$E(x)=0,2x+40+\frac{20\,000}{x}$
$E'(x)=0,2-\frac{20\,000}{x^2}$
$E'(100)=0,2-\frac{20\,000}{100^2} = 0,2-\frac{20\,000}{10\,000} = 0,2-2 =-1,8$
$E'(100)$ forteller oss at en dag det produseres 100 luer, ville produksjonskostnaden synke med 1,8 kroner per lue, dersom fabrikken skulle øke produksjonen med 1 lue.
Oppgave 3
$\lim\limits_{x \to 3} \frac{x-3}{x^2+x-12}$
$=\lim\limits_{x \to 3} \frac{x-3}{(x-3)(x+4)}$
$=\lim\limits_{x \to 3} \frac{1}{x+4}$
$=\frac{1}{7}$
Oppgave 4
$e^{2x}-e^x=2$
$(e^x)^2-e^x-2=0$
Setter $u=e^x$
$u^2-u-2=0$
$(u+1)(u-2)=0$
$u=-1 \vee u=2$
$e^x=-1 \vee e^x=2$
Forkaster det negative svaret fordi ln(-1) ikke er definert.
$ln(e^x)=ln(2)$
$x=ln(2)$
Oppgave 5
$lg(x+3)+lg\,x=lg\,a$
Setter inn x=7.
$lg(7+3)+lg\,7=lg\,a$
$lg\,10 + lg\,7=lg\,a$
$lg(10\cdot7)=lg\,a$
$lg\,70 = lg\,a$
$a=70$
Oppgave 6
a)
Eleven ønsker å finne ut hvor stor andel av en million kast med to terninger, som ender med at summen av de to terningene er 9 (i samme kast).
Linje 1: importerer "randint"-funksjonen fra "random"-biblioteket Linje 4: setter variabelen N til en million Linje 5: setter variabelen "gunstige" til null
Line 7: dette er en for-løkke, som går N ganger, altså en million ganger i dette tilfellet.
Linje 8-9 (inni for-løkka): to tilfeldige tall, a og b, genereres med "randint"-funksjonen. Tallene a og b er mellom 1 og 6 (tilsvarende 2 terninger).
Linje 10-11 (inni for-løkka): en if-setning sier at dersom summen av tallene a og b er lik 9, økes variabelen "gunstige" med 1.
Linje 13: her skrives andelen gunstige utfall ut, altså antall ganger summen av "terningene" ble 9, delt på antall forsøk (en million terningkast med to terninger).
b)
Sum 9 på to terninger er mulig å oppnå på 4 måter: 6+3, 5+4, 4+5, 3+6. Totalt er det 6*6=36 mulige utfall ved kast av to terninger.
Vi har at $P(sum\,9) = \frac{4}{36}=\frac{1}{9}$
DEL 2
Oppgave 1
a)
Velger å la x-verdiene være antall år etter 1960, og bruker regresjonsanalyse i Geogebra.
Velger en eksponentiell modell, da denne passer godt til dataene vi har. I tillegg er det usannsynlig at antall gårdsbruk i Norge blir null, så en eksponentiell modell hvor antall gårdsbruk fortsetter å avta uten å bli null, passer godt.
Modellen er $g(x)=207814\cdot 0,972^x$
b)
Skriver x=100 i Geogebra (tilsvarer 100 år etter 1960, altså 2060) og finner skjæringspunktet mellom x=100 og grafen til g. Se punkt A=(100,12061). Ifølge modellen min vil det være 12061 gårdsbruk i Norge i 2060.
c)
Bruker CAS i Geogebra og løser likningen $g'(x)=-1000$. CAS regner ut at $x=62,4$. Det vil si at ifølge modellen min, vil antall gårdsbruk i Norge avta med ca. 1000, ca. 62 år etter 1960, altså i år 2022.