1P 2022 høst LK20 LØSNING

oppgave som pdf

Diskusjon av oppgaven på matteprat

Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas

Oppgave 1

Promille er del av 1000 og prosent er del av 100. En prosent (%) er altså 10 promille (‰).

a)

Tre promille av to og en halv million:

$2500000 \cdot \frac{3}{1000} = 2500 \cdot 3 = 7500 $kr.

b)

Økningen er fra 0,3 % til 0,35 %, altså en økning på 0,05 prosentpoeng.

Oppgave 2

De ønsker å bygge: $140 m^2 + (6m \cdot 8m) = 188 m^2$

Reguleringsplanen tillater: $600 m^2 \cdot 0,3 = 180 m^2$

Det er ikke mulig, åtte kvadratmeter for mye.

Oppgave 3

a)

Se nøye på tallene. 4, 25, 49, 81, 100.

Dersom man tar kvadratroten: 2, 5, 7, 9, 10

Grafen kan representere en kvadratrot funksjon: $f(x) = \sqrt{x}$

b)

$f(16)= \sqrt{16} = 4$

$f(400)= \sqrt{400} = 20$

$f( \frac 94)= \sqrt{\frac 94} = \frac 32$

$f(-25)$ er ikke mulig da vi ikke greier å finne to like tall som ganget med hverandre blir - 25. Minus fem ganger minus fem er positiv tjuefem.

Oppgave 4

a)

Stigningstallet:

$a= \frac{y_2-y_1}{x_2-x_1} = \frac{538-159}{142-42}= \frac{379}{100} = 3,79$

Det betyr at en gallon er ca. 3,79 liter.

b)

I liter per dag blir det ca:

$3,79\cdot 42 \cdot 10^8 = 159,18 \cdot 10^8 \approx 1,6 \cdot 10^{10}$

Oppgave 4

a)

Det ser jo ganske riktig ut......

b)

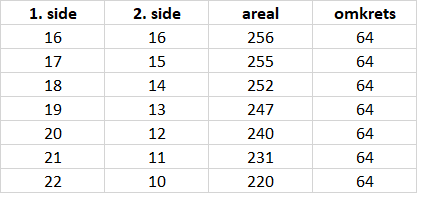
I et rektangel er to og to sider like lange (rettvinklet). Dersom vi har 64 meter til rådighet har to av sidene lengden x. Det som er igjen av lengde er da 64 - 2x fordelt på de to andre sidene, En av disse sidene blir da 32-x (har delt på to).

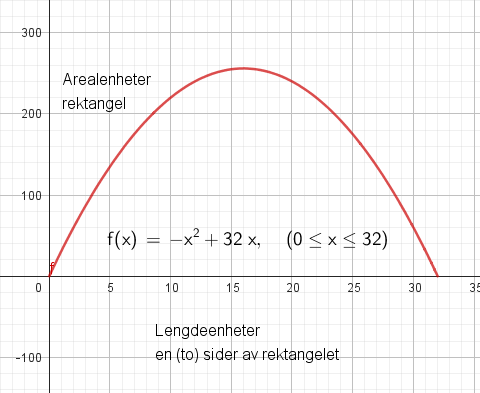
En funksjon for arealet blir da $A(x) = x \cdot (32-x)= -x^2 + 32x$