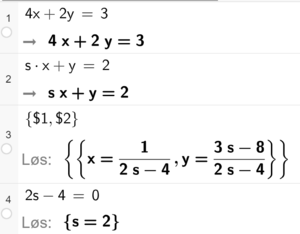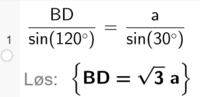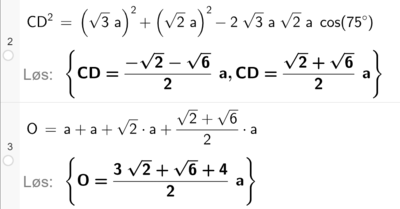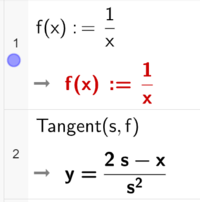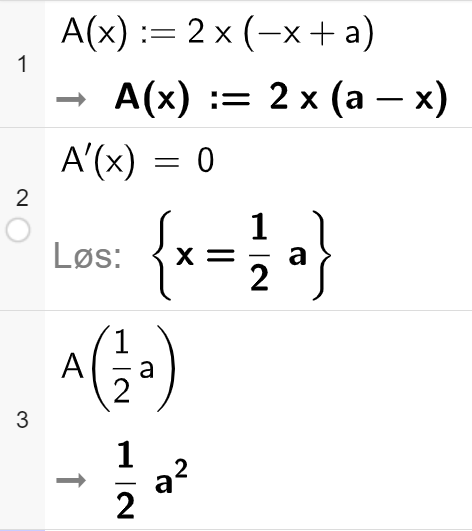1T 2021 høst LK20 LØSNING

Diskusjon av denne oppgaven på matteprat

DEL 1

Oppgave 1

Vet at stigningstallet for begge linjene er det samme, nemlig -2, siden linjene er parallelle.

Bruker ettpunktsformelen, hvor $x_1=5, y_1=-6, a=-2$

$y-y_1=a(x-x_1)$

$y-(-6)=-2(x-5)$

$y+6=-2x+10$

$y=-2x+10-6$

$y=-2x+4$ er likningen for linjen m.

Oppgave 2

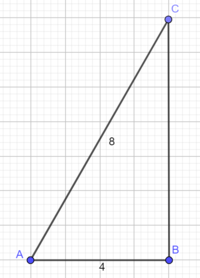
Tegner en hjelpetrekant.

Vet at $cos A = sin A = \frac{AB}{AC}=\frac{1}{2}$ og siden $AB=4$, har vi $AC=8$

Oppgave 3

Skal løse likningen $x^3+2x^2-7x+4=0$

Ser at x=1 er en løsning til likningen. Sjekker at det stemmer:

$1^3+2\cdot 1^2-7\cdot 1+4=1+2-7+4=0$

Det stemmer at x=1 er en løsning, og dermed er (x-1) en faktor. Bruker polynomdivisjon for å faktorisere resten av uttrykket.

$\quad(x^3+2x^2-7x+4):(x-1)=x^2+3x-4$

$-(x^3-x^2)$

_____________________________

$\quad\quad\quad\quad 3x^2-7x+4 $

$\quad\quad\quad -(3x^2-3x)$

_____________________________

$\quad\quad\quad\quad\quad \quad -4x+4$

$\quad\quad\quad\quad \quad -(-4x+4)$

_____________________________

$\quad\quad\quad\quad\quad\quad\quad\quad\quad 0$

Faktoriserer $x^2+3x-4=(x+4)(x-1)$

Faktoriserer hele uttrykket $x^3+2x^2-7x+4=(x+4)(x-1)(x-1)$

Tredjegradslikningen har to løsninger: $x=-4$ og $x=1$

Oppgave 4

Fra likning II har vi at $y=-2-x$

Setter dette inn i likning I:

$x^2+2x-(-2-x)=-1$

$x^2+2x+2+x=-1$

$x^2+3x+3=0$

Bruker andregradsformelen:

$x=\frac{-3\pm\sqrt{3^2-4\cdot 1\cdot 3}}{2\cdot 1}$

$x=\frac{-3\pm\sqrt{-3}}{2}$

Vi får et negativt tall under kvadratroten, så denne likningen har ingen løsning. Derfor har heller ikke likningssystemet noen løsning.

Oppgave 5

DEL 2

Oppgave 1

a)

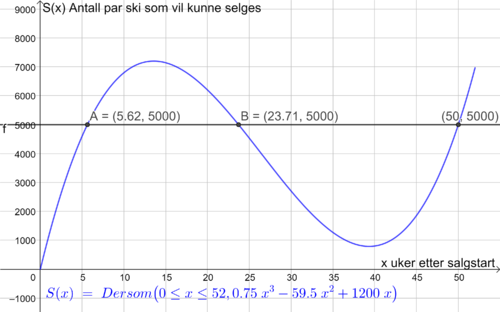
Tegner grafen til funksjonen S i Geogebra. Lager linja y=5000 og finner skjæringspunktene mellom linja og grafen til S. Ser at butikken kan selge mer enn 5000 par ski fra uke 5.6 til uke 23.7 (litt over 18 uker), og fra uke 50 til 52 (2 uker). Det vil si at butikken kan selge mer enn 5000 par ski i ca. 20 uker, ifølge modellen.

b)

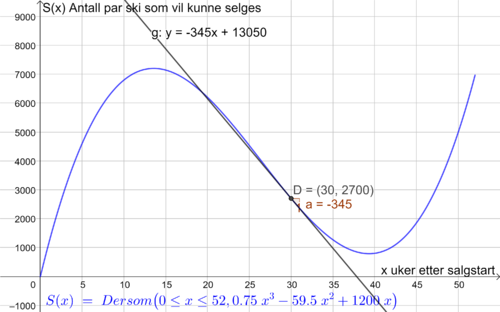
Lager punktet D=(30,S(30)), og tangenten til S gjennom punktet D ved å bruke kommandoen "Tangent". Finner stigningstallet til tangenten ved å bruke knappen "Stigning". Stigningstallet til tangenten til S (altså den momentane vekstfarten) i x=30 er -345. Det betyr at i starten av den 30. uken, synker antall par ski butikken vil kunne selge, med 345 par ski per uke.

Oppgave 2

a)

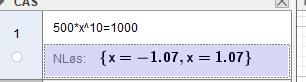
Dersom en bestand bestående av 500 dyr dobler seg lineært på 10 år ser funksjonen slik ut: L(x) = 50 x + 500

b)

Dersom bestanden øker eksponentielt får vi:

$E(x)= 500 \cdot 1,07^x$

c)

d)

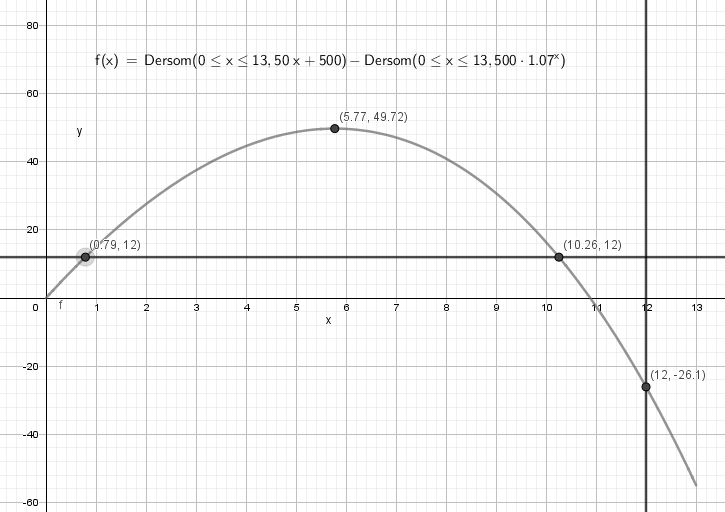
Grafen til f viser forskjellen i estimat mellom den lineære modellen og den eksponentielle, under de gitte forutsetninger. Den største forskjellen er på ca. 50 dyr, etter ca 6 år. Den praktiske tolkningen av y= 12 er ved hvilke tidspunkt den lineære modellen estimerer 12 dyr mer enn den eksponentielle. For x = 12 får vi en funksjonsverdi nær - 26. Det må tolkes som at den eksponentielle funksjonen nå har det høyeste estimatet, og etter 12 år viser den eksponentielle funksjonen ca. 26 dyr mer enn den lineære funksjonen.

Begge funksjonene, L og E skulle doble seg på 10 år. Fra figuren i c ser man at det tar nesten 11 år før E dobler seg. Det skyldes at jeg burde tatt med en desimal til i uttrykket for vekstfaktoren.

Oppgave 3

Bruker CAS i Geogebra.

Dersom s=2 ser vi at det blir null i nevner i uttrykkene x og y. Det vil da ikke være noen løsning på likningssystemet.

Oppgave 4

Bruker CAS i Geogebra.

Monica er 19 år, og Sissel er 91 år.

Oppgave 5

Bruker CAS i Geogebra.

a)

Bruker sinussetningen.

b)

Vinkelsummen i en trekant er 180 grader, så trekanten ABD er likesidet, fordi $ \angle{ADB} = \angle{DBA} = 30^o $. Vet derfor at $AB=AD=a$

Bruker cosinussetningen til å finne lengden av CD. Legger til slutt sammen lengden til alle de ytre sidene av figuren.

c)

Bruker arealsetningen i hver av de to trekantene. Legger til slutt sammen arealet i de to trekantene, og finner a når arealet av firkanten er lik $\sqrt{3}$

Forkaster det negative svaret, og har derfor at $a=-\sqrt{2}+\sqrt{6}$

Oppgave 6

a)

Bruker CAS i Geogebra.

$y=\frac{2s-x}{s^2}$

$y=\frac{2s}{s^2}-\frac{x}{s^2}$

$y=\frac{2}{s}-\frac{1}{s^2}\cdot x$

$y=-\frac{1}{s^2}\cdot x+\frac{2}{s}$

som skulle vises.

b)

Bruker CAS i Geogebra. Setter inn x = 0 i likningen for tangenten for å finne y-verdien til punkt B. Setter inn y = 0 i likningen for tangenten for å finne x-verdien til punkt A.

Vi har $A=(2s,0)$ og $B=(0,\frac{2}{s})$

c)

Bestemmer arealet av $\Delta OAB$:

$A=\frac{1}{2}\cdot g\cdot h$

$A=\frac{1}{2}\cdot 2s\cdot \frac{2}{s}$

$A=2$

Oppgave 7

a)

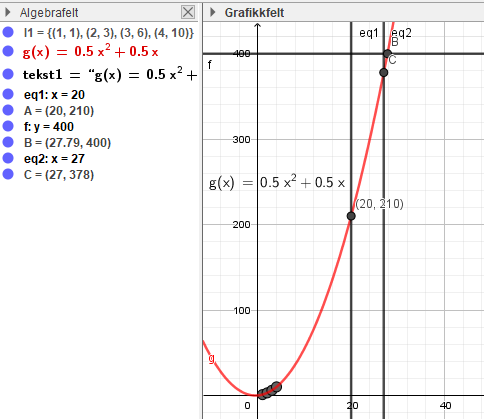
Finner funksjonsuttrykket ved regresjon i Geogebra. Lager linja x = 20 og bruker "skjæring mellom to objekt" mellom denne linja og polynomfunksjonen.

Ser at 20 etasjer krever 210 bokser, se punkt A.

b)

Skriver y=400 og bruker "skjæring mellom to objekt" mellom denne linja og polynomfunksjonen.

Marius kan lage maksimalt 27 etasjer med 400 bokser, se punkt B i oppgave a). Til det trenger han 378 bokser, se punkt C i oppgave a).

c)

Bruker polynomregresjon av 3. grad:

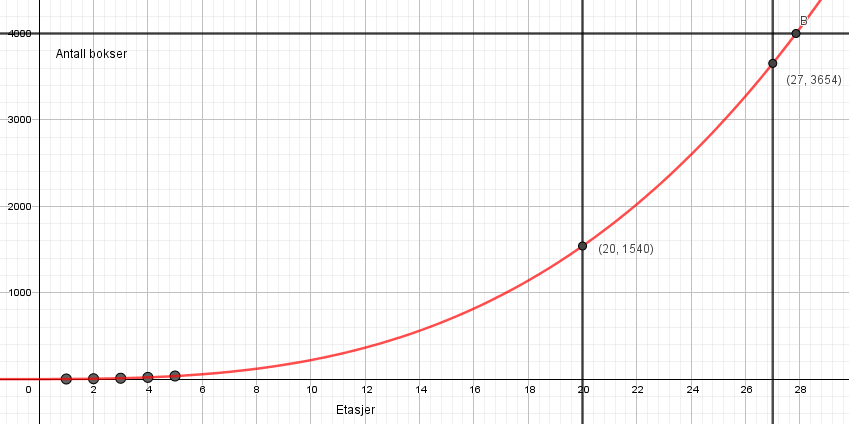
Lager linja x = 20 og bruker "skjæring mellom to objekt" mellom denne linja og polynomfunksjonen.

20 etasjer krever 1540 bokser. Se figur.

d)

Skriver y=4000 og bruker "skjæring mellom to objekt" mellom denne linja og polynomfunksjonen.

Det er 27 etasjer i det største tårnet Maria kan lage med 4000 bokser, se figuren i oppgave c).

Oppgave 8

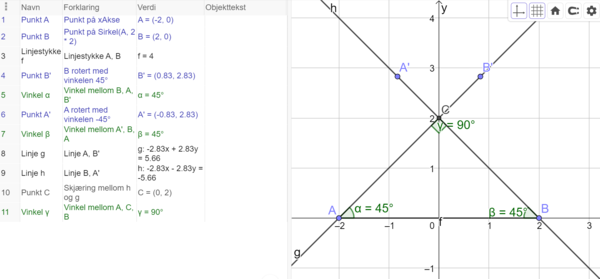
"Skal vi først sette $a=2$ og tegne trekanten? Vinkel A og vinkel B er jo $45^{\circ}$, så det klarer vi. Kan vi bruke datamaskinen til dette?"

Jeg er enig i at vinkel A og vinkel B er $45^{\circ}$, siden vinkel C er $90^{\circ}$, og summen av vinklene i en trekant er $180^{\circ}$. Jeg er også enig i at det går an å bruke Geogebra på datamaskinen til å tegne trekant ABC med en gitt lengde for $a$. Gjør dette nedenfor:

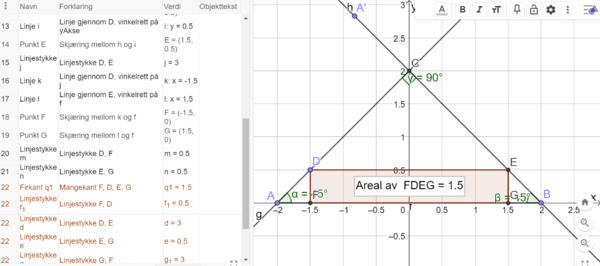
"Ja, og så tegner vi ulike rektangler som er innskrevet i trekanten og finner arealene av disse. Etterpå kan vi tegne trekanten når $a=3$. Vi må være litt systematiske. Her er en tabell vi kan bruke som utgangspunkt. Kanskje vi ser et mønster? En sammenheng mellom verdien av $a$ og det største arealet rektangelet kan få?"

Bruker Geogebra til å tegne ulike rektangler innskrevet i trekanten og finner arealene av disse. Jeg endrer deretter lengden på $a$, og gjentar dette. Jeg noterer arealene i en tabell, slik Andreas og Markus foreslår.

Jeg ser en sammenheng mellom verdien av $a$ og det største arealet $A_{max}$ rektangelet kan få, nemlig:

$A_{max}=\frac{a^2}{2}$

Sjekker at formelen min stemmer med verdiene i tabellen:

når a=2 $A_{max}=\frac{2^2}{2}=2$

når a=3 $A_{max}=\frac{3^2}{2}=4,5$

når a=4 $A_{max}=\frac{4^2}{2}=8$

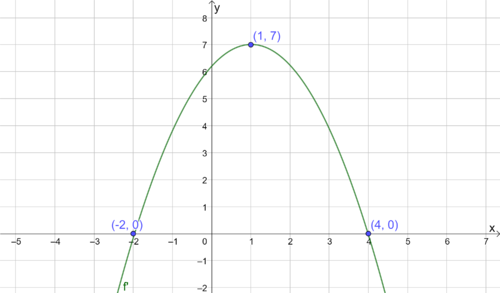
"Etterpå må vi prøve å bevise at sammenhengen vi kommer fram til gjelder generelt, altså for alle verdier av a. Trine og Nora sier at de har funnet ut at den rette linja gjennom B og C er gitt ved $y=-x+a$. Kan det stemme?"

Det stemmer at den rette linja gjennom B og C er gitt ved $y=-x+a$. Jeg kaller skjæringspunktet mellom høyden i trekanten og x-aksen for P. Skjæringspunktet med y-aksen (konstantleddet) er a, fordi $PC=PB=a$, fordi $\Delta PBC$ er en likebeint trekant siden $\angle B = \angle PCB = 45^{\circ}$. Stigningstallet er -1 fordi linja går fra punktet (0,a) til (a,0). Stigningstallet er da lik $\frac{a}{-a}=-1$.

"Arealet av rektangelet er jo lengde · bredde. Vil det da bli $2x\cdot y$ ?"

Jeg er også enig i dette, fordi lengden av rektangelet er det dobbelte av x-verdien til punktet som utgjør "nedre høyre hjørne" i rektangelet. Bredden på rektangelet er y-verdien til de "øvre hjørnene" i rektangelet.

Nå kan jeg bevise at sammenhengen $A_{max}=\frac{a^2}{2}$ gjelder generelt, for alle verdier av a.

Vi har $A=2x\cdot y = 2x\cdot (-x+a)$

Bruker CAS i Geogebra til å finne x-verdien i toppunktet til funksjonen, altså x-verdien når A'(x)=0. Finner deretter y-verdien i toppunktet, altså verdien til det største mulige arealet, uttrykt ved a. Vi ser at det største arealet er $\frac{1}{2}a^2 = \frac{a^2}{2}$, som skulle vises.