Løsning del 2 utrinn Vår 21

oppgaven del 2 som pdf

Diskusjon av oppgaven på matteprat

Oppgave 1

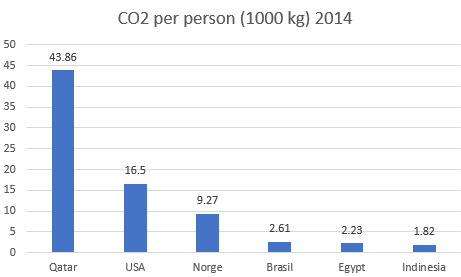
a)

b)

Variasjonsbredde : $43,86 - 1,82 = 42,04$

c)

Nedgang i prosent fra 2014 til 2018:

$\frac {8,3}{9,27} \cdot 100 \% = 89,5$. Nedgangen var på ca. 10,5%.

Oppgave 2

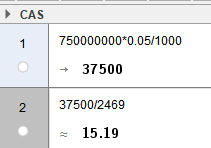
a)

15 tonn/ min multiplisert med 60 min: $15 \cdot 60 = 900$ tonn i timen.

b)

$15 \cdot 2 + 50 \cdot 2 + 20 \cdot 3 + 65 \cdot 3 = 30 + 100 + 60 + 195 = 385$

Hun fikk 385 kroner i pant.

c)

Det blir et "plastfjell" ca 15 ganger høyere enn galdhøpiggen.

Oppgave 3

a)

1,9 dollar ganger 9,1245 NOK er 17 kroner og 33 ører. De som lever på dette daglig lever i ekstrem fattigdom (FN).

b)

Fra tabell og tekst ser man at 15,048 millioner utgjør 5,7% av befolkningen. Hele befolkningen blir da:

$\frac{15,048}{5,7}\cdot 100 = 264$ millioner mennesker.

Oppgave 6

a)

Langs x og y retning er ikke avstanden problematisk. Det skulle være minst 360 meter mellom mølletårnene. I x og y retning er det 500 meter. Nå står det ingenting i oppgaven om tårnenes radius. Vi antar derfor at de er punkter. Langs diagonalene blir avstanden 353,6 meter. Dette er 6,4 meter mindre enn avstandskravet. I tillegg vet vi at tårnene har en utstrekning, slik at avstanden fra tårnvegg til tårnvegg blir mindre i virkeligheten. Nå må det legges til at med vindmøller i hjørnene vil parken i praksis dekke et område betydelig større enn en kvadratkilometer.

Dersom reglene er absolutte, og politikere og byråkrater har tenkt å følge dem, kan parken ikke bygges slik, selv om det var små marginer.

b)

Farten på tuppen av møllevingen: $v = \frac st = \frac{2 \pi r \cdot 20 \cdot 60 m}{1h} = 452,4 km/h$

Oppgave 7

Oppgave 8

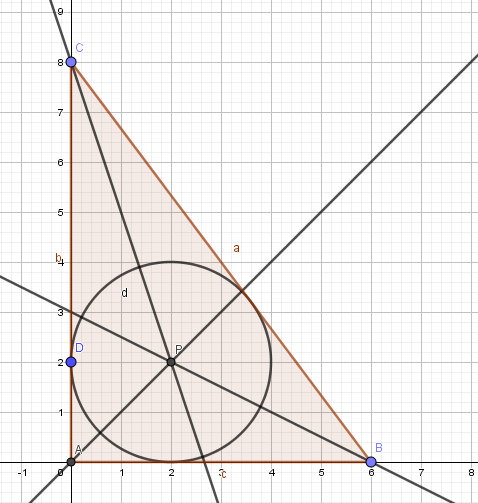
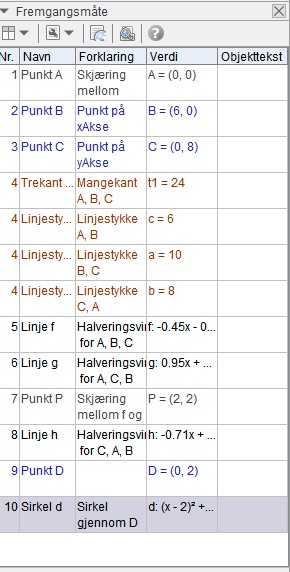
a)

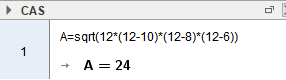
$s = \frac {a+b+c}{2} = \frac{10+8+6}{2} = 12$

Arealet av trekanten er 24.

b)

Den store trekantenc med en innskrevet sirkel, består av tre mindre trekanter, alle med høyde r. Arealet blir:

$\frac{r \cdot a}{2} + \frac{r \cdot b}{2} + \frac{r \cdot c }{2} = A $

$2A = r (a + b + c)$

$r = \frac {2A}{a + b + c}$